Jump back to chapter selection.

Table of Contents

4.1 Kerr Effect and Self-Phase Modulation
4.2 Self-Focusing and Filamentation
4.3 Solitons - Nonlinear Schrödinger Equation
4.4 Self-Steepening
4.5 Nonlinear Propagation in a Saturable Absorber or Saturable Amplifier

4 Nonlinear Pulse Propagation

This chapter discusses nonlinear pulse propagation to the extent that it is relevant to ultrafast lasers. For another perspective on nonlinear optics, especially with a focus on magnetism, please read here.

4.1 Kerr Effect and Self-Phase Modulation

The intensity-dependent refractive index is given by:

where $n_0$ is the linear refractive index, $n_2$ is the nonlinear refractive index coefficient, and $I$ is the intensity of the light. This phenomenon is known as the optical Kerr effect. The value of $n_2$ is typically of the order of ${10}^{-16}{\text{cm}}^2/\text{W}$ for many solid-state materials in the near-infrared (near-IR). Since this is approximately three orders of magnitude higher than the nonlinear refractive index of air at atmospheric pressure, $n_2$ for air can usually be neglected in many situations. However, at the high intensities encountered within ultrafast laser cavities or in focused beams, the Kerr effect in air and other optical media becomes significant and cannot be ignored.

For a laser beam with a constant beam area propagating through a Kerr medium of length $L_{\mathrm{K}}$, the total phase shift accumulated is $\phi (t)=k{L}_{\mathrm{K}}n(I(t))$. The linear part is ${\phi }_0=k{n}_0{L}_{\mathrm{K}}$. The intensity-dependent part, or nonlinear phase shift, is:

Let us redefine the nonlinear phase shift experienced by the pulse envelope as ${\phi }_2(t)$. If the pulse envelope is $A(t)$ such that $I(t)=|A(t){|}^2$ (with appropriate normalisation of $A(t)$), then:

where $k_0={\omega }_0/c$ is the vacuum wave number at the carrier frequency ${\omega }_0$, and $\delta$ is the self-phase modulation (SPM) coefficient, defined as:

The electric field after propagating through the Kerr medium can be written as:

where $A_{\text{in}}(t)$ is the input complex envelope $A(0,t)$.
The output envelope $A(L_K,t)$ is then $A_{\text{in}}(t)e^{i\delta |A_{\text{in}}(t){|}^2}$. For small SPM ($\delta |A_{\text{in}}(t){|}^2\ll 1$), we can linearise the exponential:

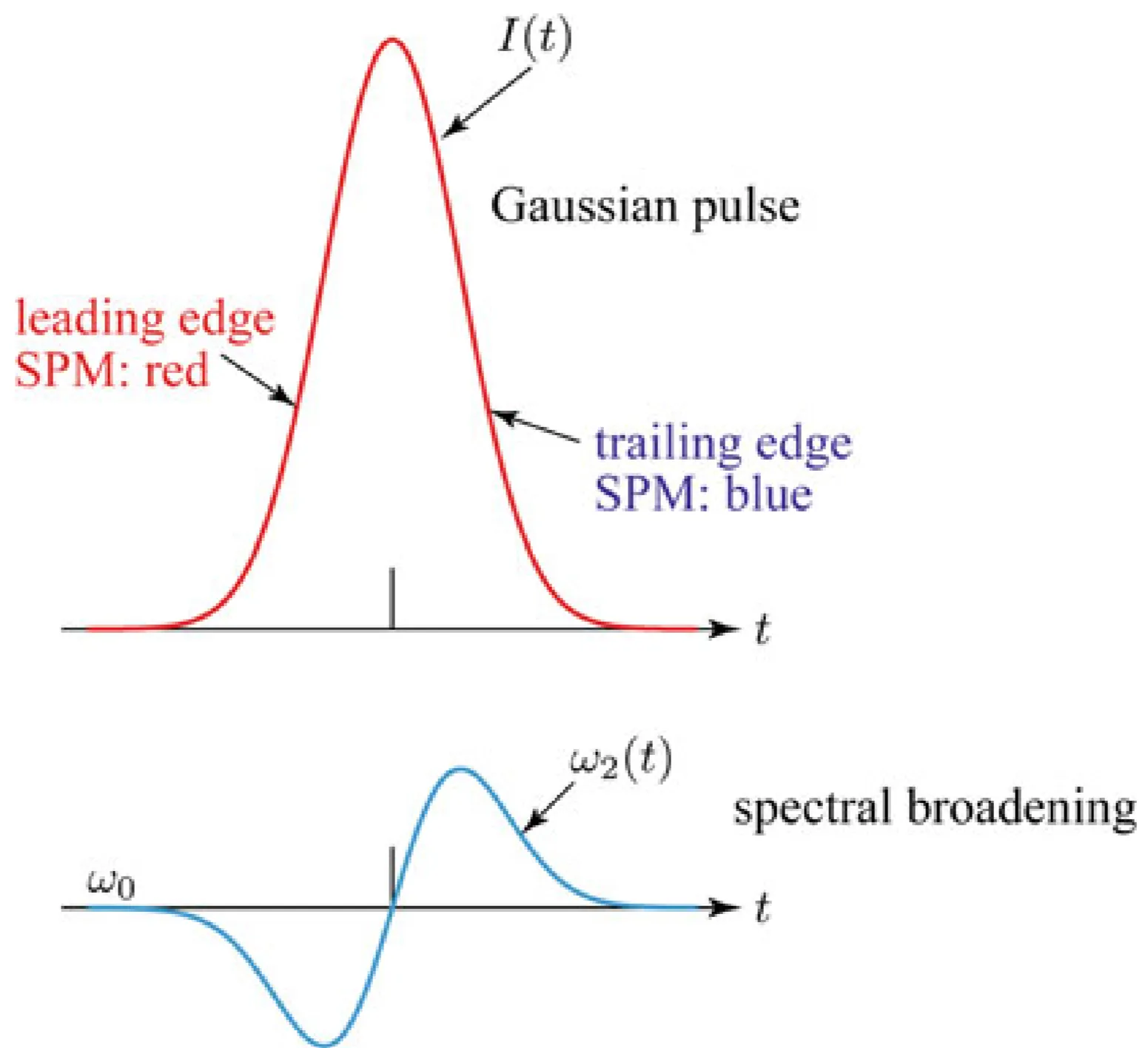
SPM broadens the pulse spectrum because it introduces an instantaneous frequency shift. The total phase of the field can be written as $\mathrm{\Phi }(t)={\omega }_{0}t-k_0{n}_0{L}_K+{\phi }_2(t)$. The instantaneous frequency is $\omega (t)=d\mathrm{\Phi }(t)/dt={\omega }_0+d{\phi }_2(t)/dt$. The instantaneous frequency shift due to SPM is:

Assuming $n_2>0$ (so $\delta >0$):
At the leading edge of the pulse, intensity is rising, so $dI(t)/dt>0$, leading to $\mathrm{\Delta }{\omega }_{\text{inst}}(t)>0$ (blue-shift, increase in frequency).
At the trailing edge of the pulse, intensity is falling, so $dI(t)/dt<0$, leading to $\mathrm{\Delta }{\omega }_{\text{inst}}(t)<0$ (red-shift, decrease in frequency).
This is often described as "red before blue" on the pulse for positive $n_2$.

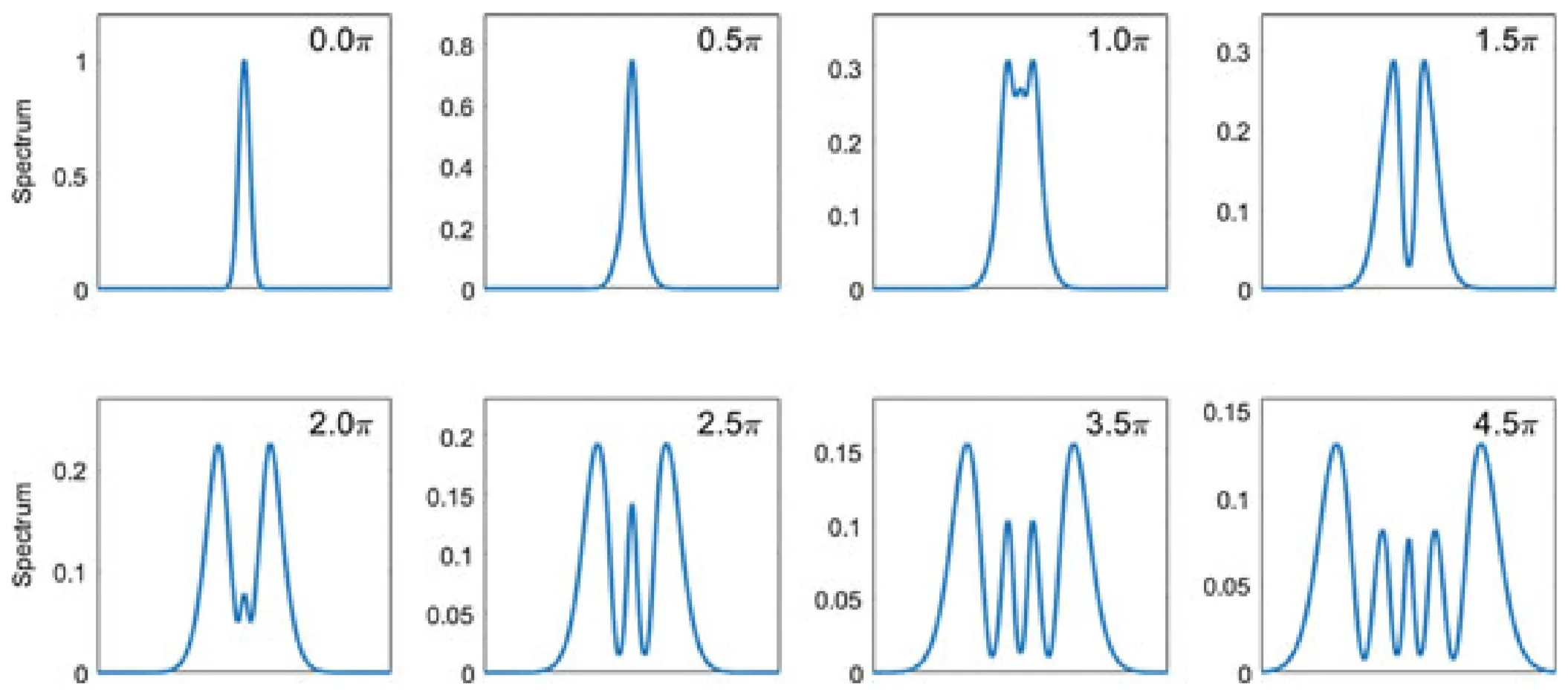
SPM-induced spectral broadening often leads to an oscillatory structure in the spectrum, particularly for strong SPM:

The number of oscillation peaks $M$ (or more precisely, the number of new spectral lobes generated on each side of the original spectrum) is related to the maximum nonlinear phase shift ${\phi }_{2,\text{max}}$:

where $I_{\text{peak}}$ is the peak intensity of the pulse.

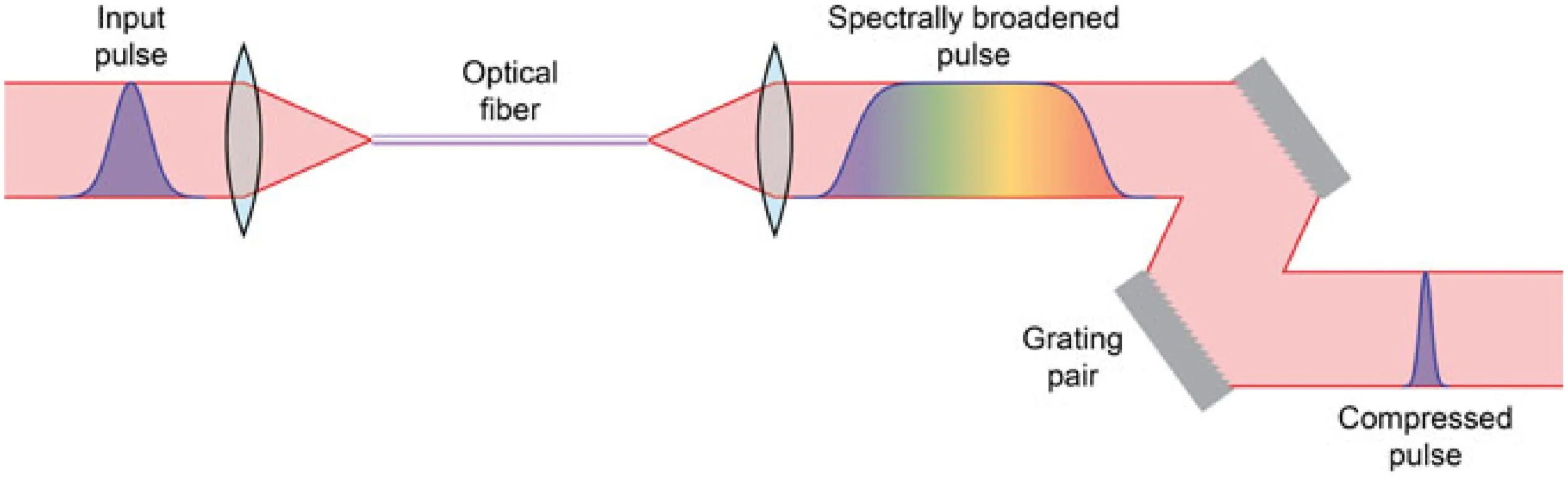
4.1.1 Pulse Compression

Spectral broadening induced by SPM can be utilised to compress initially transform-limited pulses. A common method involves propagating a pulse through an optical fibre (where $n_2$ can be significant over long lengths) to broaden its spectrum via SPM:

If the fibre has positive group-delay dispersion (GDD) and $n_2>0$, the pulse will acquire a positive chirp (lower frequencies leading higher frequencies). After spectral broadening, a subsequent element providing anomalous (negative) GDD, such as a grating pair or prism pair compressor, can compensate for this chirp and shorten the pulse in time.
It is important to note that SPM typically introduces a chirp that is only approximately linear in the central, high-intensity region of the pulse. Only this quasi-linear part of the chirp can be effectively compensated by a standard compressor (which provides GDD, a quadratic spectral phase). The remaining uncompensated (non-linear) chirp and the modified spectral shape mean that the compressed pulse width may be broader than the minimum transform limit suggested by the broadened spectral width, and often introduces temporal wings or pedestals on the compressed pulse. This can degrade the quality (specifically, the peak power and contrast) of the compressed pulse.

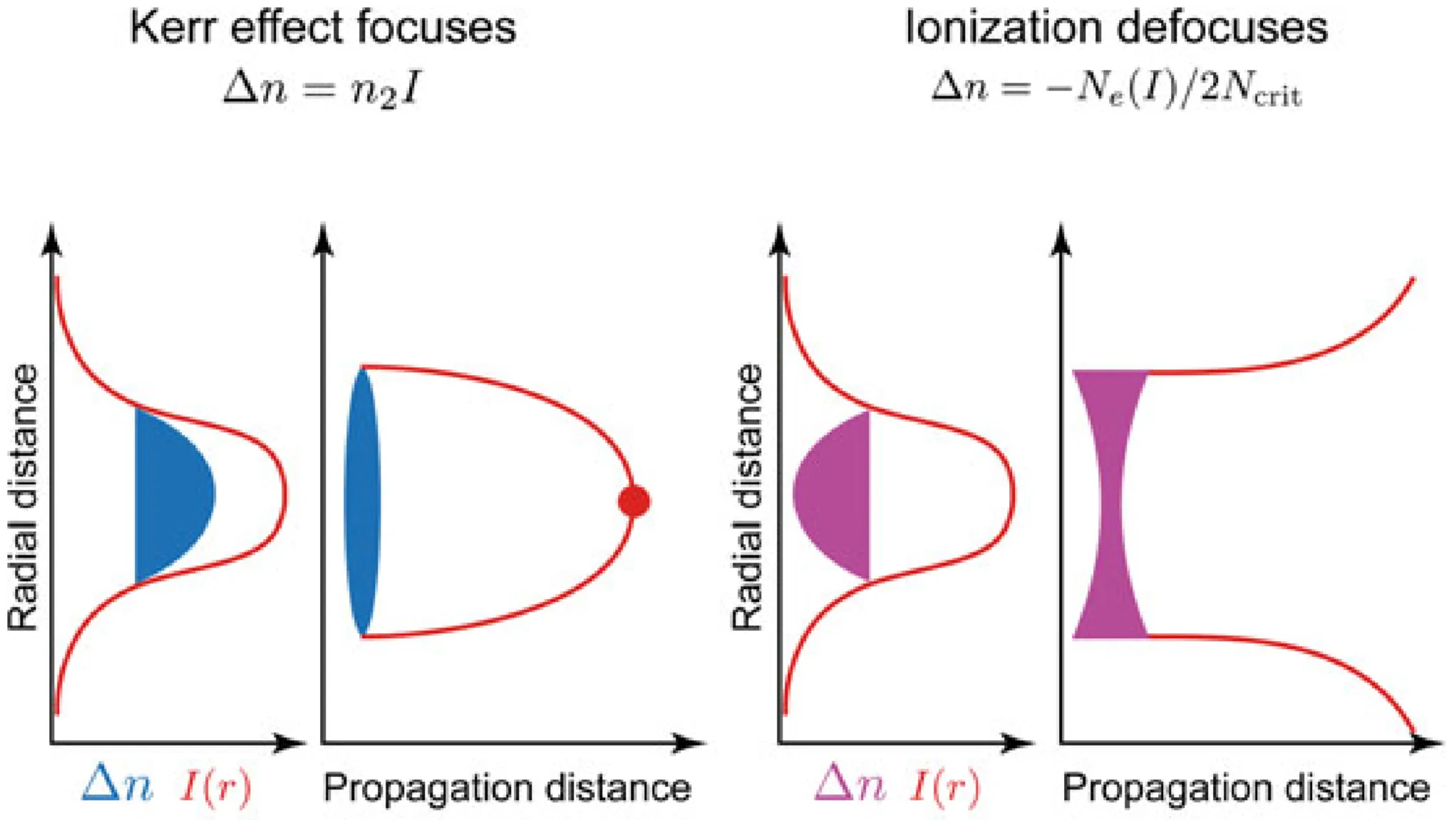
4.2 Self-Focusing and Filamentation

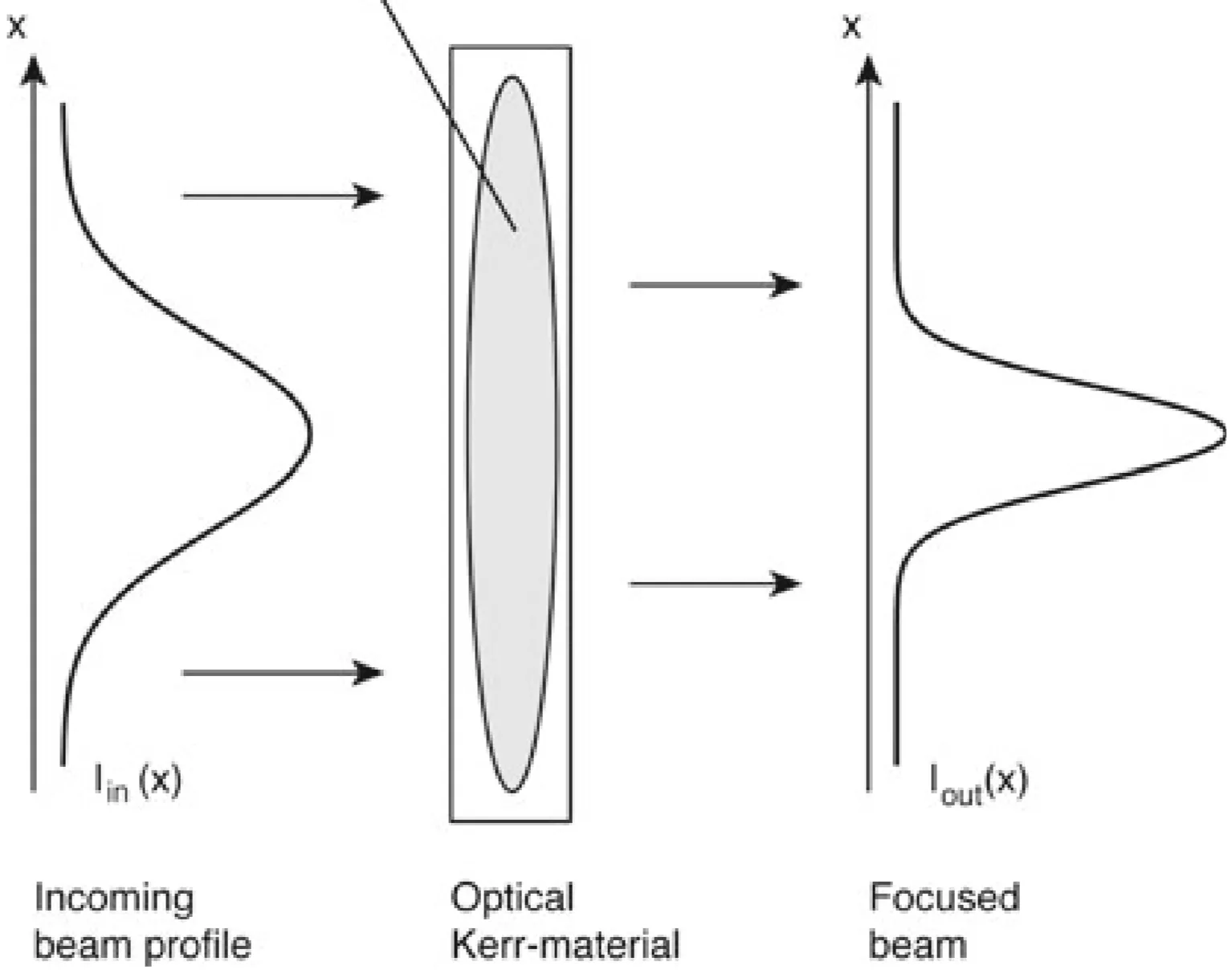
Self-Focusing

Due to the Kerr effect ($n(I)=n_0+n_{2}I$), an intense laser beam with a transverse intensity profile (typically peaked on-axis) induces an intensity-dependent refractive index profile in the medium. If $n_2>0$, the refractive index is higher where the intensity is higher (on-axis). This effectively creates a focusing (positive) lens within the material itself:

For a sufficiently thin Kerr medium of length $L_{\mathrm{K}}$ (such that the beam radius $w$ does not change significantly within it), and a Gaussian transverse beam profile:

where $r^2=x^2+y^2$. For regions close to the axis ($r\ll w$), this can be approximated as:

This results in a parabolic refractive index variation transverse to the propagation direction:

where $n_{\text{axis}}=n_0+n_2{I}_{\mathrm{peak}}$ is the on-axis refractive index and $\mathrm{\Delta }{n}_p=n_2{I}_{\mathrm{peak}}$ is the maximum nonlinear index change. This parabolic index profile corresponds to a focusing lens with an effective focal length $f_{\text{NL}}$ given by (for a thin lens approximation):

where $A_s$ is a scaling factor (often close to $n_0$) accounting for the exact beam shape and higher-order effects neglected in the simple parabolic expansion.

To avoid catastrophic self-focusing and material damage in high-power laser systems, the accumulated nonlinear phase shift on-axis, quantified by the B-integral, should generally be kept below a critical value (typically $B<3\text{ to }5$ radians):

Filamentation

When the power of a laser beam exceeds a certain critical power $P_{\text{cr}}$, self-focusing can become dominant. In gases, Kerr-induced self-focusing increases the local optical intensity. As the intensity rises dramatically due to the collapsing beam, other nonlinear effects, primarily multi-photon ionisation (MPI) or tunnel ionisation of the gas, become significant. This ionisation creates a plasma (free electrons). The plasma contributes negatively to the refractive index ($\mathrm{\Delta }{n}_{\text{plasma}}<0$), effectively acting as a defocusing lens.

This interplay between Kerr self-focusing and plasma defocusing can lead to a dynamic balance, resulting in the formation of a filament: a long, narrow channel of high intensity that can propagate over distances much longer than the Rayleigh range of a normally diffracting beam. The high intensity within the filament broadens the pulse spectrum significantly via self-phase modulation (SPM), often to such an extent that a supercontinuum spanning much of the visible spectrum (white light) is emitted. This can transform an initially infrared laser pulse into a 'white-light laser' source within the filament.
The critical power for self-focusing in a bulk medium can be approximated as:

where ${\lambda }_0$ is the central vacuum wavelength, $n_0$ is the linear refractive index, and ${\alpha }_f$ is a dimensionless constant that depends on the beam profile (for a Gaussian beam, ${\alpha }_f\approx 1.86$ to $3.77$ depending on definition conventions). In gases, before complete beam collapse and optical breakdown occur, the intensity typically clamps at a level where MPI balances further focusing.

4.3 Solitons - Nonlinear Schrödinger Equation

A wave packet propagating through a linear dispersive medium will generally change its shape (disperse), as discussed in Chapter 2. This is a linear effect. However, if the medium also exhibits an intensity-dependent refractive index (Kerr effect), leading to self-phase modulation (SPM), these two effects—dispersion and SPM—can interact. For certain pulse shapes and under specific conditions, they may cancel each other out, allowing a pulse to propagate without changing its temporal shape. Such self-sustaining wave packets are known as solitons. The propagation of optical solitons in fibres is often described by the nonlinear Schrödinger equation (NSE).

Solitons are extremely important for the generation and propagation of ultrashort electromagnetic pulses, particularly in optical fibres. Consequently, they have been extensively studied for applications in optical communications, laser physics (fibre lasers), and nonlinear optics.

Optical solitons (specifically bright temporal solitons in fibres) are pulses for which the spectral broadening and chirp induced by SPM (due to positive $n_2$) are precisely balanced by anomalous group-delay dispersion (GDD $<0$, or $k_n^{″}<0$). This balance allows the pulse to propagate without temporal broadening (or compression) over long distances. True solitons also exhibit particle-like collision properties: they can pass through each other and emerge unchanged except for a possible phase shift and positional shift.

4.3.1 Derivation

First, recall the equation for the evolution of the pulse envelope's spectrum $\tilde{A}(z,\mathrm{\Delta }\omega )$ in a dispersive medium within the SVEA, considering terms up to second-order dispersion (GDD):

where $z$ is the propagation distance (replacing $L_d$). This can be written as a differential equation:

Transforming back to the time domain (using $\mathrm{\Delta }\omega \leftrightarrow i\frac{\partial }{\partial t^{\prime }}$ in a retarded time frame $t^{\prime }=t-k_n^{\prime }z$):

This describes pulse shaping due to GDD.
Now, we include the effect of SPM. The nonlinear phase shift accumulated over a small distance $dz$ is $d{\phi }_2={\delta }^{\prime }|A{|}^{2}dz$, where ${\delta }^{\prime }=k_0{n}_2$. So, $A(z+dz,t^{\prime })\approx A(z,t^{\prime })e^{i{\delta }^{\prime }|A(z,t^{\prime }){|}^{2}dz}\approx A(z,t^{\prime })(1+i{\delta }^{\prime }|A(z,t^{\prime }){|}^{2}dz)$.
This leads to $\frac{\partial A(z,t^{\prime })}{\partial z}{|}_{\text{NL}}=i{\delta }^{\prime }|A(z,t^{\prime }){|}^{2}A(z,t^{\prime })$.
Combining the GDD and SPM contributions:

This is a common form of the nonlinear Schrödinger equation (NSE). The sign of the nonlinear term depends on the convention for ${\phi }_2(t)$. If ${\phi }_2(t)=+\delta |A{|}^2$ as used earlier for SPM spectral broadening, the nonlinear term is $+i(k_0{n}_2)|A{|}^{2}A$.
Standard form often uses ${\beta }_2=k_n^{″}$ and $\gamma =n_2{\omega }_0/(c{A}_{\text{eff}})$ (where $A$ is field not intensity, relating to power). If $A$ is normalised such that $|A{|}^2$ is intensity, then $\gamma \approx k_0{n}_2$.
The NSE often written as:

So, if $k_n^{″}$ is used for ${\beta }_2$, then $i\frac{k_n^{″}}{2}\frac{{\partial }^{2}A}{\partial (t^{\prime }{)}^2}$ is the dispersion term. For the nonlinear term, $+i{k}_0{n}_2|A{|}^{2}A$ is consistent with positive $n_2$ and seeking balance with $k_n^{″}<0$.
We assumed $n_2$ is not frequency-dependent (instantaneous nonlinearity). Higher-order dispersion terms are also neglected.

4.3.2 Solution of the NSE: The Fundamental Soliton

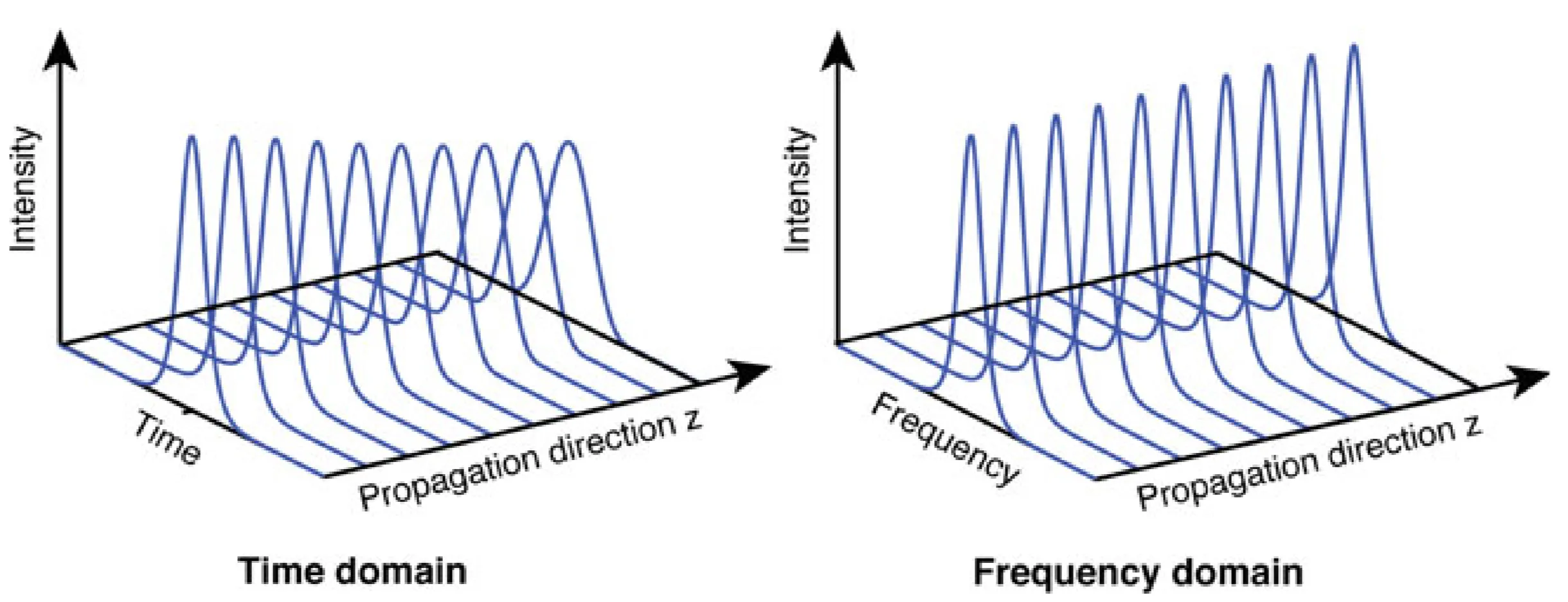
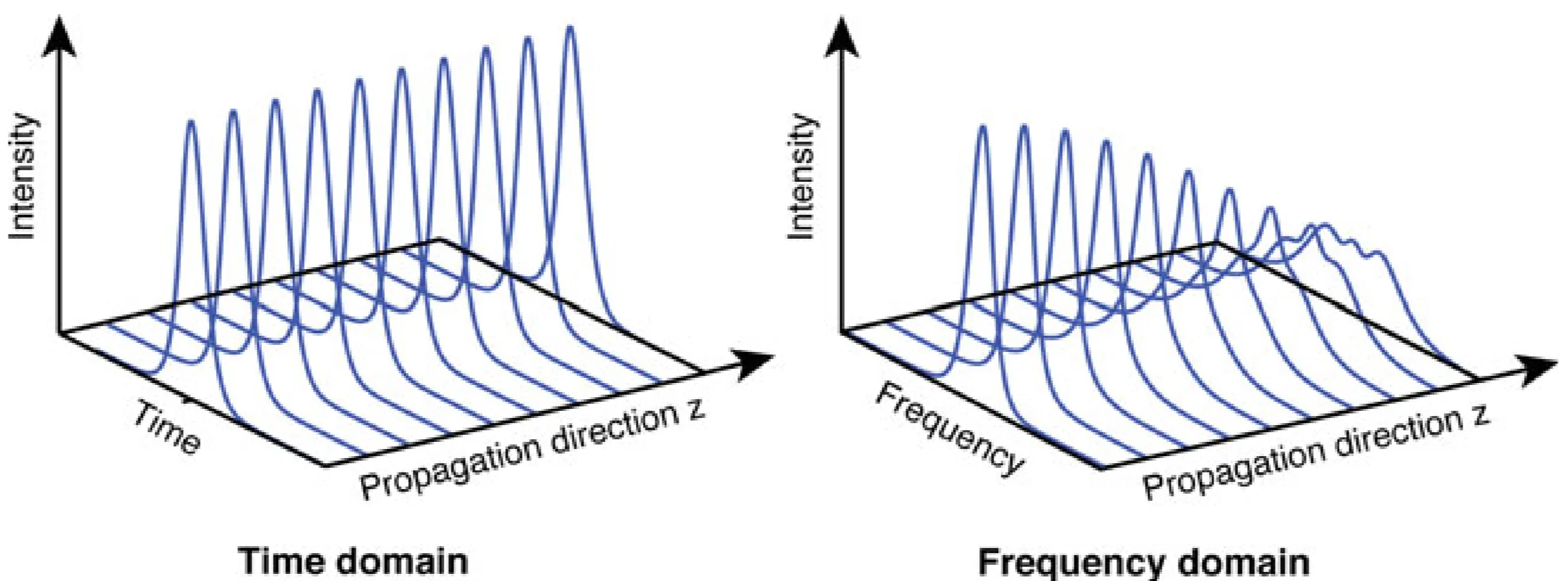
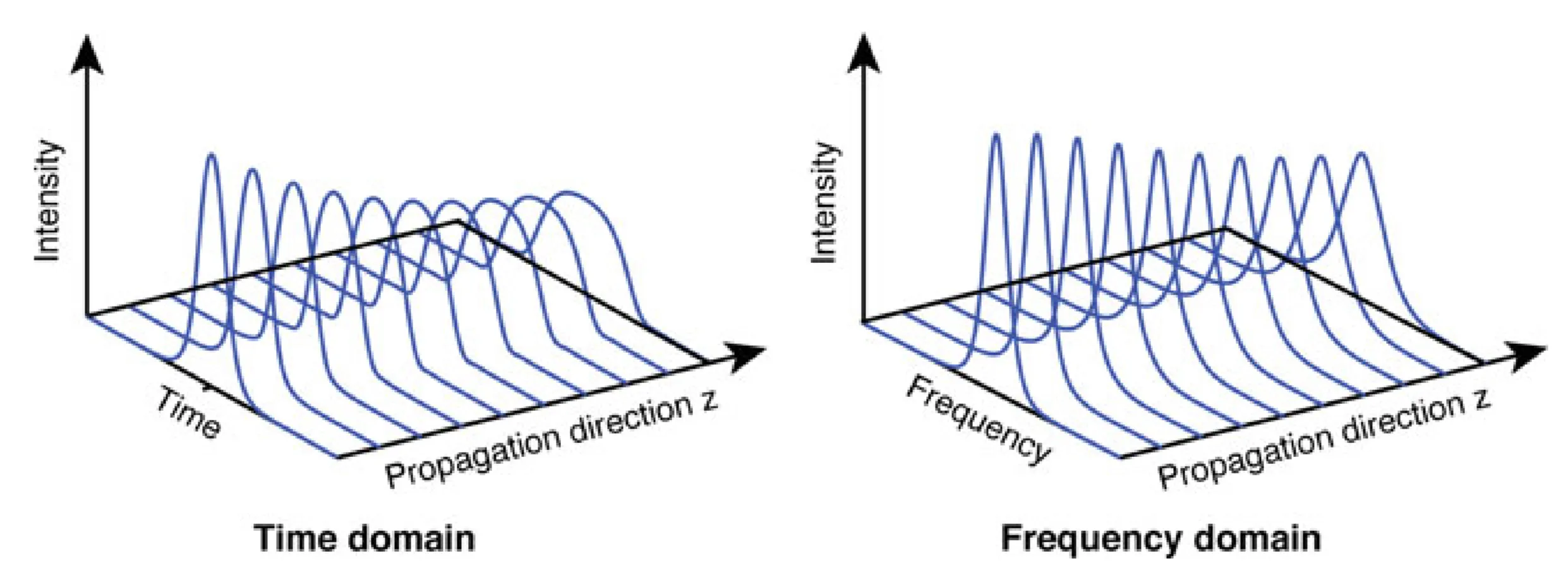
The interplay between GDD ($k_n^{″}$) and SPM (via $n_2$) governs pulse evolution:

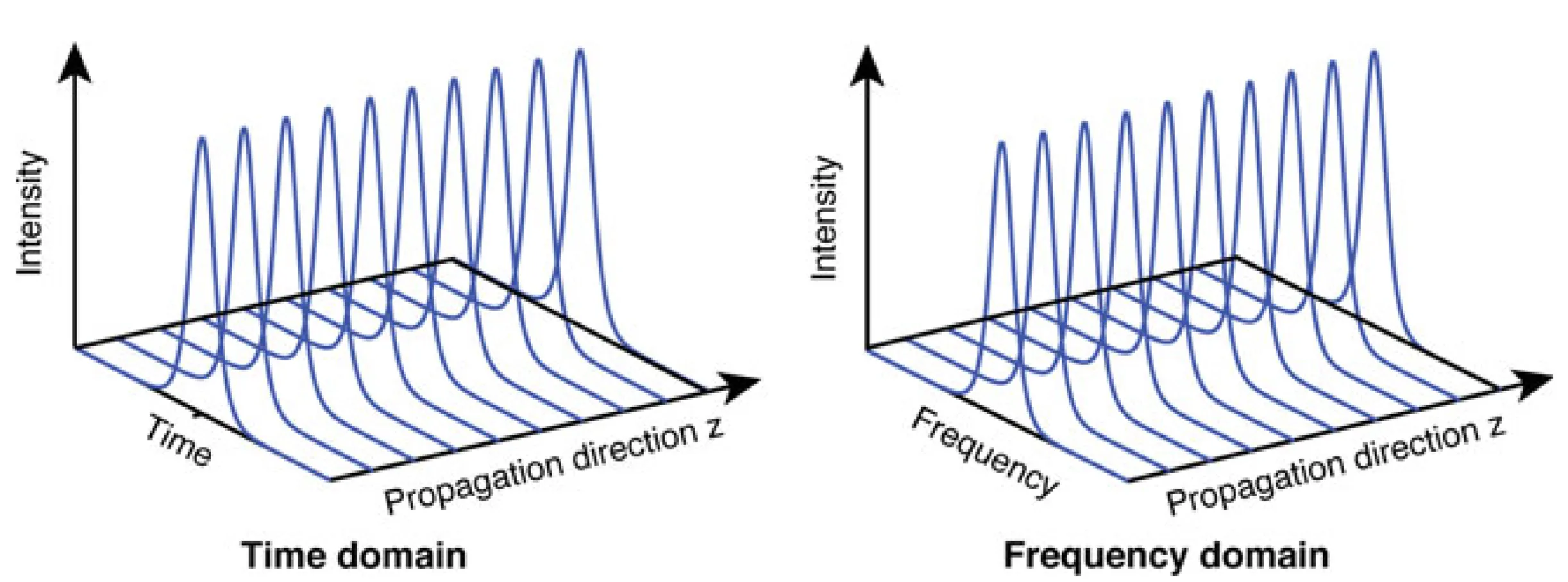
1. $k_n^{\prime \prime }\ne 0,n_2=0$: Linear propagation. An initially transform-limited pulse broadens temporally due to GDD (positive or negative $k_n^{″}$), while its spectral width remains unchanged. The spectral phase changes.
2. $k_n^{\prime \prime }=0,n_2\ne 0$: No GDD, only SPM. A transform-limited pulse maintains its temporal intensity profile (if no other effects like self-steepening are present) but its spectrum broadens due to SPM.
3. $k_n^{\prime \prime }>0$ (normal GDD), $n_2>0$: Positive SPM generates new lower frequencies (red-shifted) on the leading edge and higher frequencies (blue-shifted) on the trailing edge. Normal GDD means $v_g(\text{red})>v_g(\text{blue})$. Thus, red components at the leading edge advance further, while blue components at the trailing edge are further retarded. An initially transform-limited pulse broadens rapidly and develops a strong positive chirp.
4. $k_n^{\prime \prime }<0$ (anomalous GDD), $n_2>0$: Positive SPM still generates red-shift on leading edge and blue-shift on trailing edge. However, anomalous GDD means $v_g(\text{blue})>v_g(\text{red})$. This tends to pull back the leading (red) edge and advance the trailing (blue) edge, counteracting the SPM-induced chirp. For specific pulse shapes and intensities, a balance can be achieved where the pulse propagates without changing its temporal or spectral shape: a soliton forms.

These cases are illustrated below, with the last figure showing soliton propagation:

The NSE admits soliton solutions. The fundamental (N=1) soliton has a temporal envelope shape:

where ${\tau }_s$ is a characteristic duration parameter. The FWHM pulse duration is ${\tau }_p\approx 1.7627{\tau }_s$. This pulse is transform-limited, with $\mathrm{\Delta }{f}_p{\tau }_p\approx 0.3148$.
The parameters are related by $A_0^2=\frac{|k_n^{″}|}{(k_0{n}_2){\tau }_s^2}$ (assuming $k_n^{″}<0$ and $n_2>0$).
The phase term ${\varphi }_0(z)=\frac{|k_n^{″}|}{2{\tau }_s^2}z=\frac{1}{2}(k_0{n}_2)A_0^{2}z$.

The pulse fluence $F_p=\int I(t^{\prime })d{t}^{\prime }=A_0^2\int {\mathrm{sech}}^2(t^{\prime }/{\tau }_s)d{t}^{\prime }=A_0^2[{\tau }_s\tanh (t^{\prime }/{\tau }_s){]}_{-\mathrm{\infty }}^{\mathrm{\infty }}=2A_0^2{\tau }_s=2I_p{\tau }_s$.
The soliton duration can be related to material parameters and pulse energy/fluence. A key feature is that the soliton's parameters (shape, duration, peak power) are fixed by the balance, and it propagates without distortion in an ideal lossless fibre.

The neglect of higher-order terms means this simplest soliton only balances GDD and SPM. For negative GDD ($k_n^{″}<0$), since $v_g=1/k_n^{\prime }$ and $d{k}_n^{\prime }/d\omega =k_n^{″}<0$, $k_n^{\prime }$ decreases with $\omega$, so $v_g$ increases with $\omega$. Thus, a "blue" soliton (higher carrier frequency) moves faster than a "red" soliton. This allows solitons to interact and pass through each other, emerging with their shapes intact but with possible phase and position shifts.

4.3.3 Solution of the NSE: Higher-Order Solitons

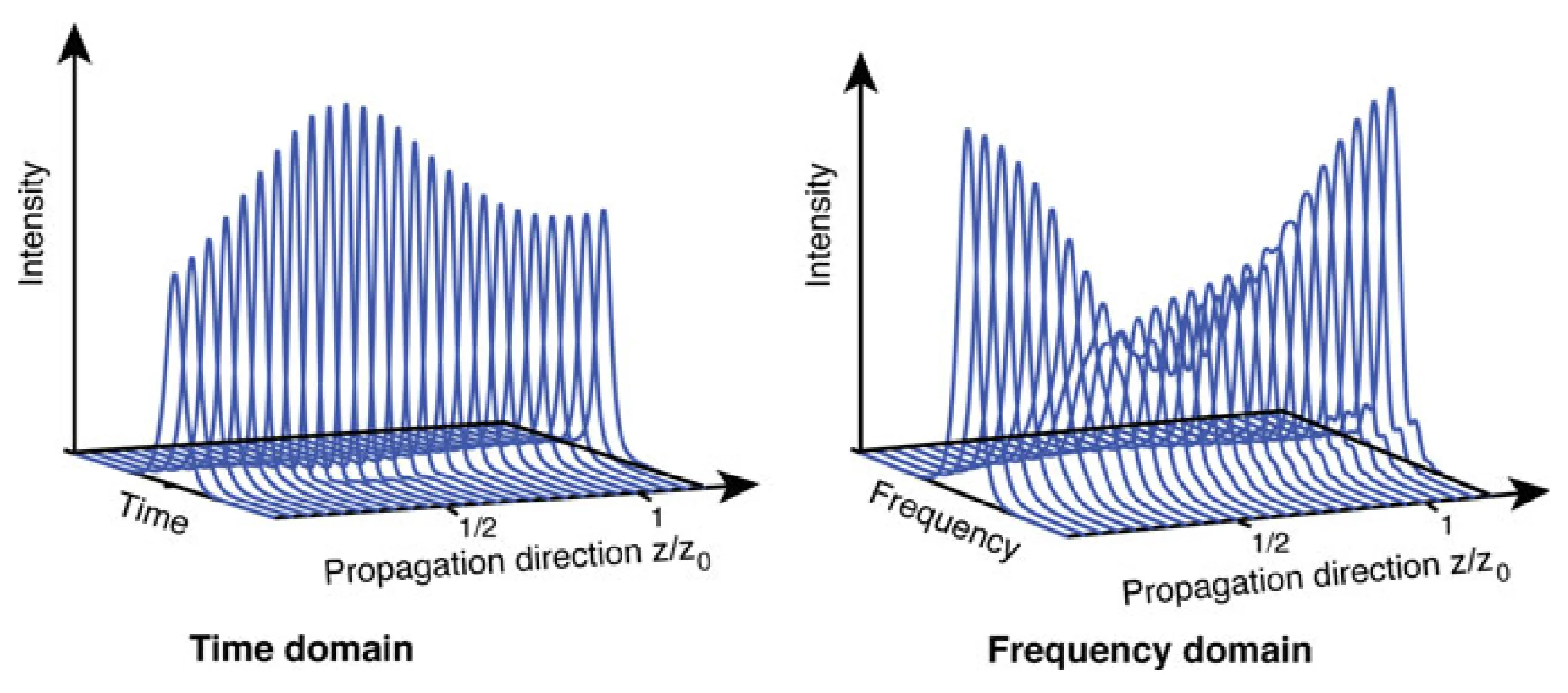
For input pulse energies that are integer multiples of the fundamental soliton energy, higher-order solitons (N=2, 3, ...) can form. These are not simple superpositions but bound states of N fundamental solitons. Unlike the fundamental soliton, a higher-order soliton undergoes periodic changes in its temporal shape and spectrum during propagation:

The soliton period $z_0$ is a characteristic length over which these changes occur. It is often defined as the distance over which the nonlinear phase shift of the fundamental soliton changes by $\pi /2$:

Higher-order solitons can be used for pulse compression if the fibre length is chosen appropriately (e.g., a fraction of $z_0$). Any part of the initial pulse energy not forming the soliton(s) can be shed as dispersive waves (continuum).

4.3.4 Optical Communication with Solitons

Skipped for now.

4.3.5 Periodic Perturbations of Solitons

Periodic perturbations (like those from amplifiers in a long-haul communication system or periodic gain/loss in a laser cavity) can affect soliton stability. The perturbed NSE is:

where $\xi \ll 1$ is the perturbation strength and $z_a$ is the perturbation period.
If the perturbation $u(z,t^{\prime })$ is small, $A\approx A_s+u$. Linearising for $u$ can lead to resonant growth of $u$ if the perturbation period $z_a$ is comparable to the soliton period $z_0$. The condition to avoid strong resonance effects (average soliton regime) is typically $z_a\ll z_0$. Since $z_0\sim {\tau }_s^2$, shorter pulses require shorter perturbation periods for stability.

4.4 Self-Steepening

For ultrashort pulses (durations below approximately $100\text{fs}$), higher-order dispersion (beyond GDD) and additional nonlinear effects become important. The simple NSE needs modification. The spectral width of such pulses can become comparable to the carrier frequency, making some SVEA assumptions questionable. Also, for very broad spectra, stimulated Raman scattering can transfer energy between frequency components (typically red-shifting the pulse). Incorporating a delayed nonlinear response and higher-order effects leads to the generalised nonlinear Schrödinger equation (GNSE):

(Note: signs for $k_n^{″}$ and $k_n^{‴}$ depend on NSE convention; ${\gamma }_{NL}\approx k_0{n}_2$).
The term $\frac{i}{{\omega }_0}\frac{\partial }{\partial t^{\prime }}(|A{|}^{2}A)$ is responsible for self-steepening. $T_R$ relates to the Raman response.

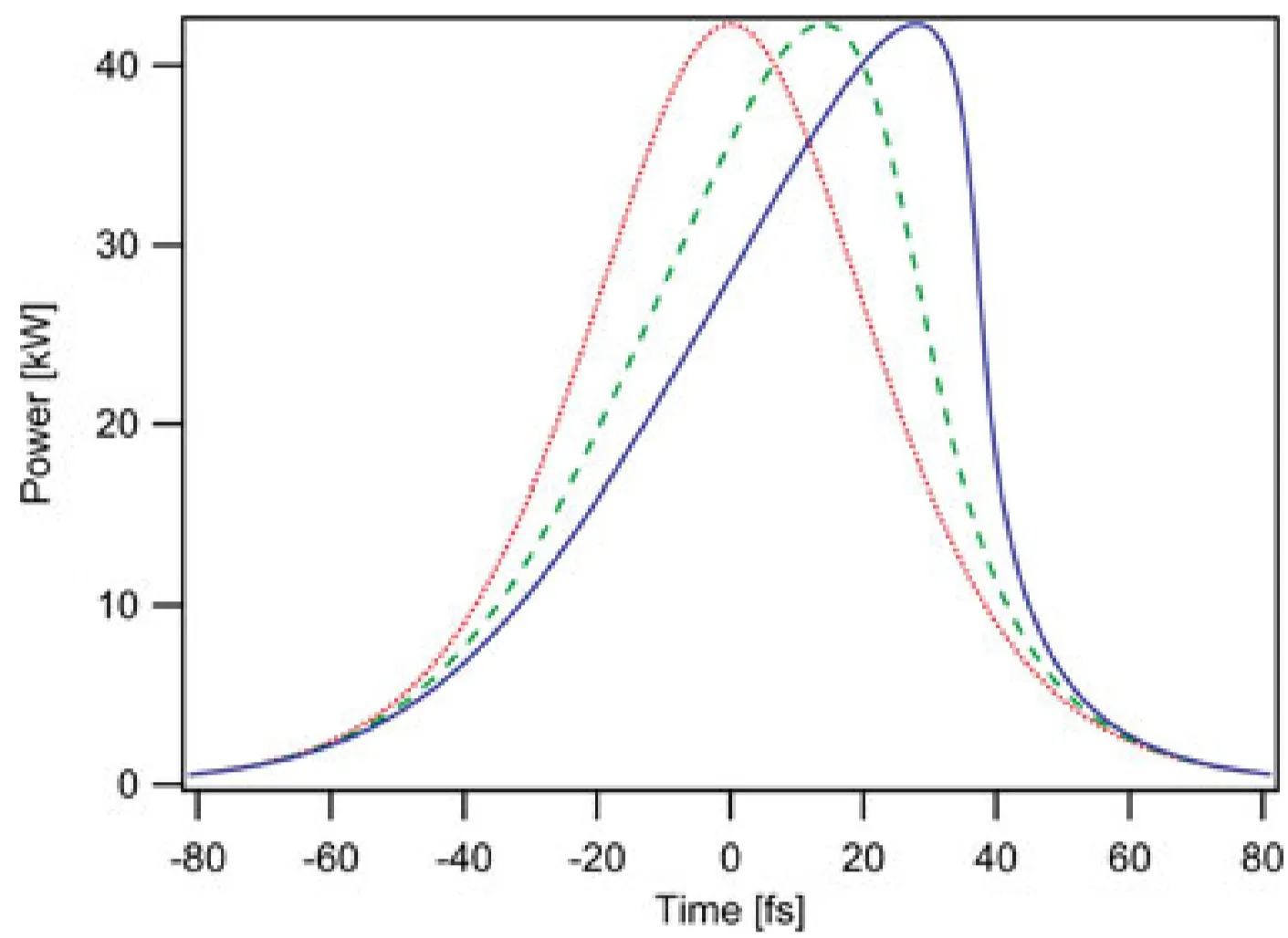
Self-steepening arises from the intensity dependence of the group velocity. It causes the peak of an intense pulse to travel slower than its wings (if $d{n}_g/dI>0$, which can happen), leading to an asymmetric steepening of the trailing edge of the pulse and an optical shock formation if dispersion is weak. It also introduces asymmetry into SPM-broadened spectra.

4.4.1 Optical Shock Front

Considering only self-steepening (no dispersion or Raman), the trailing edge of an intense pulse becomes progressively steeper with propagation distance $z$. This is because the higher intensity parts of the pulse experience a different group velocity than lower intensity parts.

This can eventually lead to the formation of an optical shock, where the intensity drops abruptly. SPM-induced spectral broadening becomes asymmetric, typically more pronounced on the blue side (higher frequencies) due to the steepened trailing edge. The shock distance depends on pulse duration and intensity; for femtosecond pulses, it can be on the order of metres or less in some media. In practice, dispersion usually acts to regularise the shock front, preventing an infinitely steep edge from forming.

4.5 Nonlinear Propagation in a Saturable Absorber or Saturable Amplifier

This section introduces concepts fundamental for understanding passive mode-locking (covered in Chapter 8).
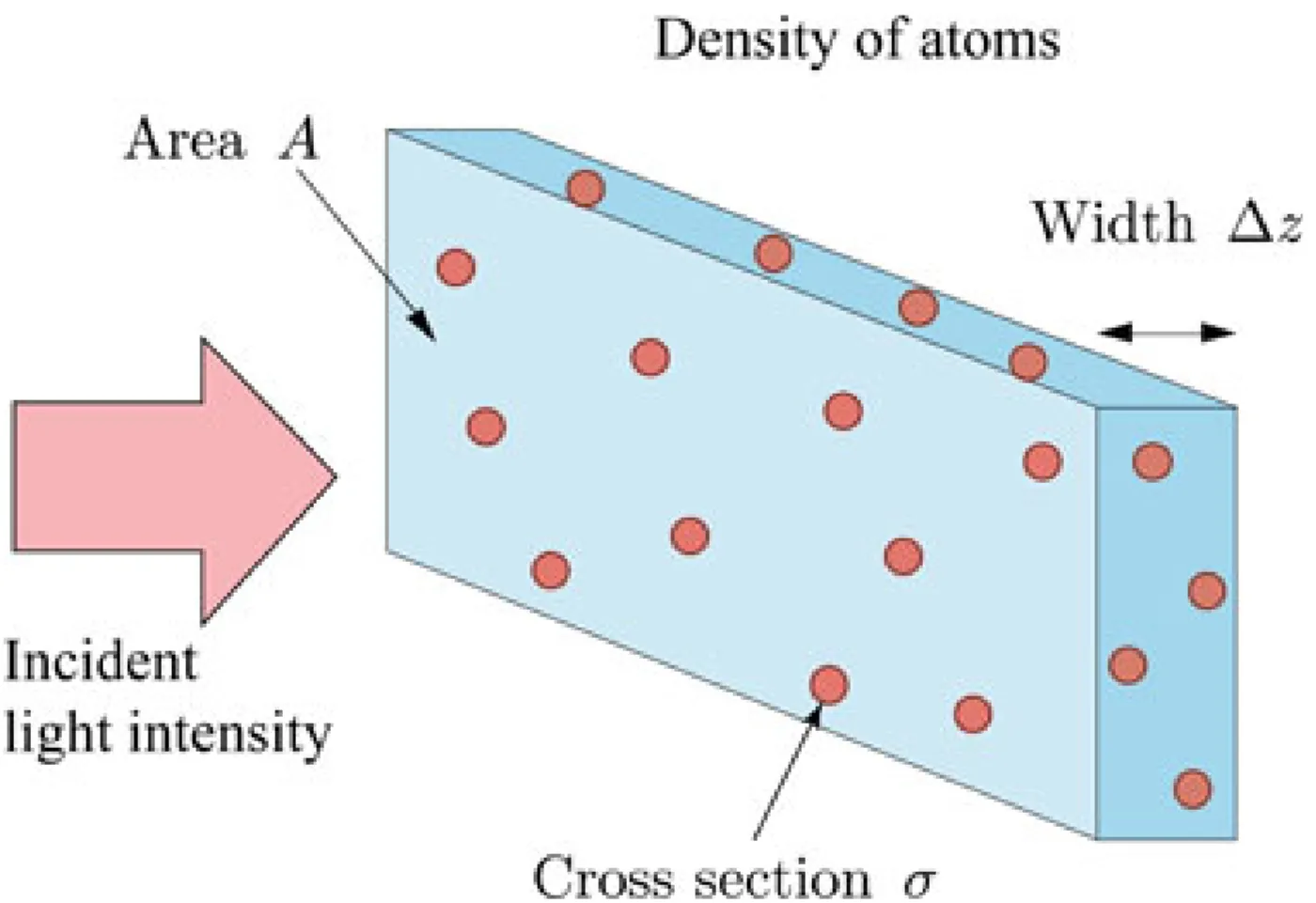
Consider a homogeneously broadened solid-state laser medium, describable as a two-level atomic system. The rate equations lead to a gain that saturates with increasing light intensity. The intensity-dependent gain coefficient $g(I)$ (for intensity) is often written as:

where $g_0$ is the small-signal gain coefficient (for instance, $g_0=(N_2-N_1){\sigma }_{\text{gain}}$ where $N_2,N_1$ are population densities of upper/lower levels, ${\sigma }_{\text{gain}}$ is stimulated emission cross-section), and $I_{\text{sat}}$ is the saturation intensity:

where $\hslash \omega$ is photon energy, and ${\tau }_L$ is the upper-state lifetime (related to recovery of gain).

4.5.1 Saturable Absorber

A saturable absorber is a material whose absorption decreases with increasing light intensity. While many materials exhibit saturation at very high intensities, for laser applications (like passive mode-locking), materials are needed that saturate at intensities typical within laser cavities. Key parameters are:

1. Operating wavelength range.
2. Dynamic response time (recovery time).
3. Saturation intensity $I_{\text{sat,abs}}$ and saturation fluence $F_{\text{sat,abs}}$.

For a simple two-level atomic system, the intensity absorption coefficient $\alpha (I)$ is:

where ${\alpha }_0$ is the unsaturated (small-signal) absorption coefficient. A saturable absorber has high loss at low intensity and low loss at high intensity. The saturation intensity is defined analogously to that for gain, using the absorption cross-section ${\sigma }_{\text{abs}}$ and effective lifetime. Since stimulated emission and absorption probabilities are related, $I_{\text{sat,abs}}$ for a two-level system can be similar to $I_{\text{sat,gain}}$ if the transition is the same.

4.5.2 Nonlinear Pulse Propagation in a Saturable Absorber or Amplifier

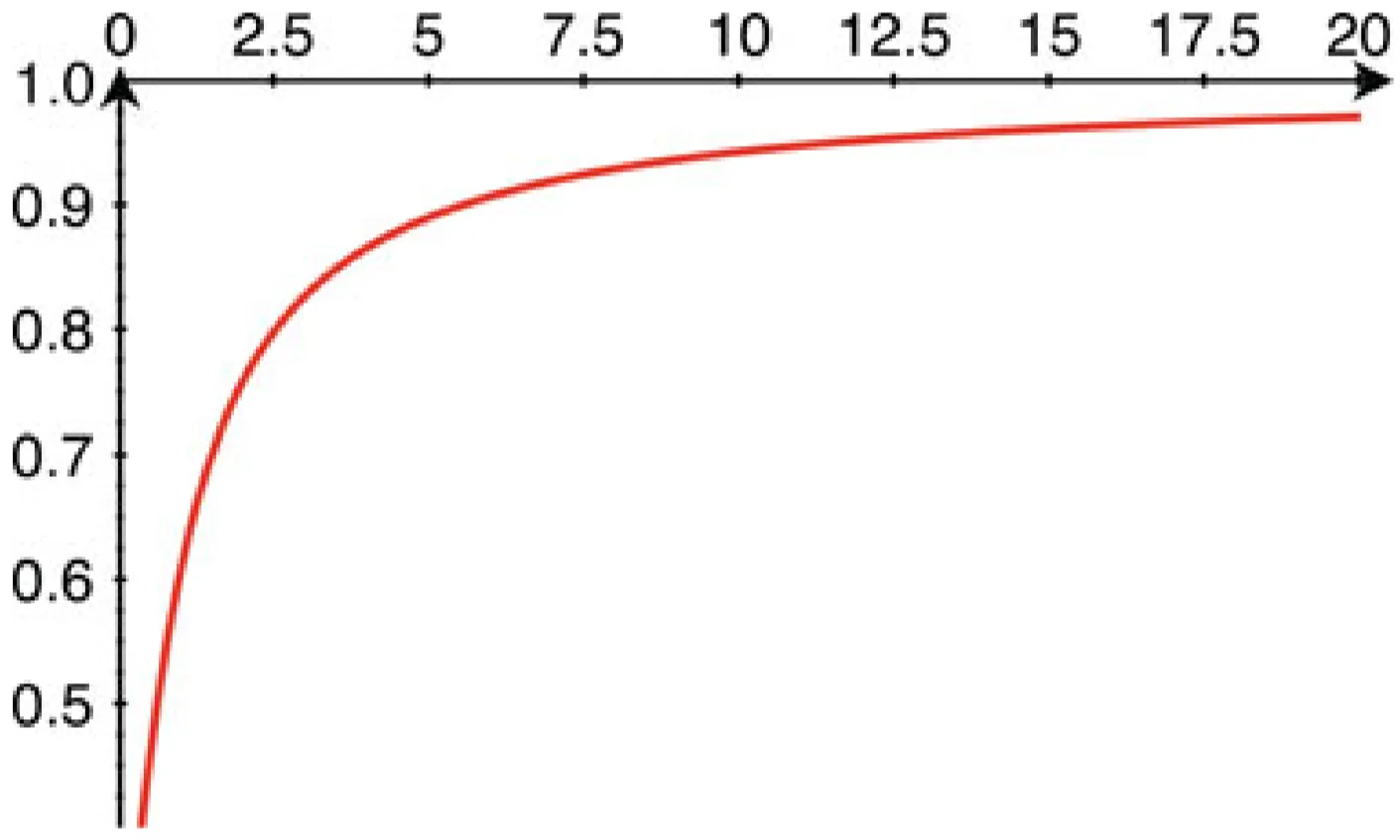
Since absorption/gain is intensity-dependent, pulse propagation becomes nonlinear. For a CW beam, the intensity transmission $T=I_{\text{out}}/I_{\text{in}}$ through an absorbing medium of thickness $d$ with saturable absorption $\alpha (I)$ follows:

For $I_{\text{in}}\ll I_{\text{sat,abs}}$, this simplifies to Beer's Law: $T\approx e^{-{\alpha }_{0}d}$.

If absorption/amplification were purely linear ($\alpha ,g$ independent of $I$), the pulse shape would remain unchanged (if bandwidth is sufficient). With nonlinear effects, the pulse shape changes. For instance, in a saturable amplifier, the leading edge of a pulse experiences high, unsaturated gain. As it propagates and amplifies, it depletes the stored energy (reduces population inversion), thus saturating the gain. Consequently, the trailing edge of the pulse experiences significantly less gain. This leads to asymmetric amplification, often shifting the pulse peak forward and steepening its leading edge. Conversely, a saturable absorber preferentially attenuates the lower-intensity wings of a pulse more than its high-intensity peak, which can lead to pulse shortening.
These intensity-dependent changes in gain/absorption are also accompanied by intensity-dependent changes in the refractive index, via the Kramers-Kronig relations.