Jump back to chapter selection.

Table of Contents

3.1 Prism Coupling
3.2 Grating Coupling
3.3 Excitation Using Highly Focused Optical Beams

3 Excitation of Surface Plasmon Polaritons at Planar Interfaces

Surface plasmon polaritons (SPPs) propagating at the flat interface between a conductor and a dielectric are essentially two-dimensional electromagnetic waves. Their confinement is a consequence of their propagation constant $\beta$ being greater than the wave number $k=k_0\sqrt{{\epsilon }_d}$ of light in the adjacent dielectric medium (where ${\epsilon }_d$ is the dielectric permittivity of the dielectric), or $\beta >k_0\sqrt{{\epsilon }_d}$. This condition leads to evanescent decay of the SPP fields on both sides of the interface. Therefore, direct excitation of SPPs by three-dimensional light beams incident from the dielectric onto a smooth metal surface is not possible, as the in-plane wave vector component of the incident light ($k_x=k_0\sqrt{{\epsilon }_d}\sin \theta$) is always smaller than $\beta$. Special techniques for phase-matching are required to overcome this momentum mismatch.

3.1 Prism Coupling

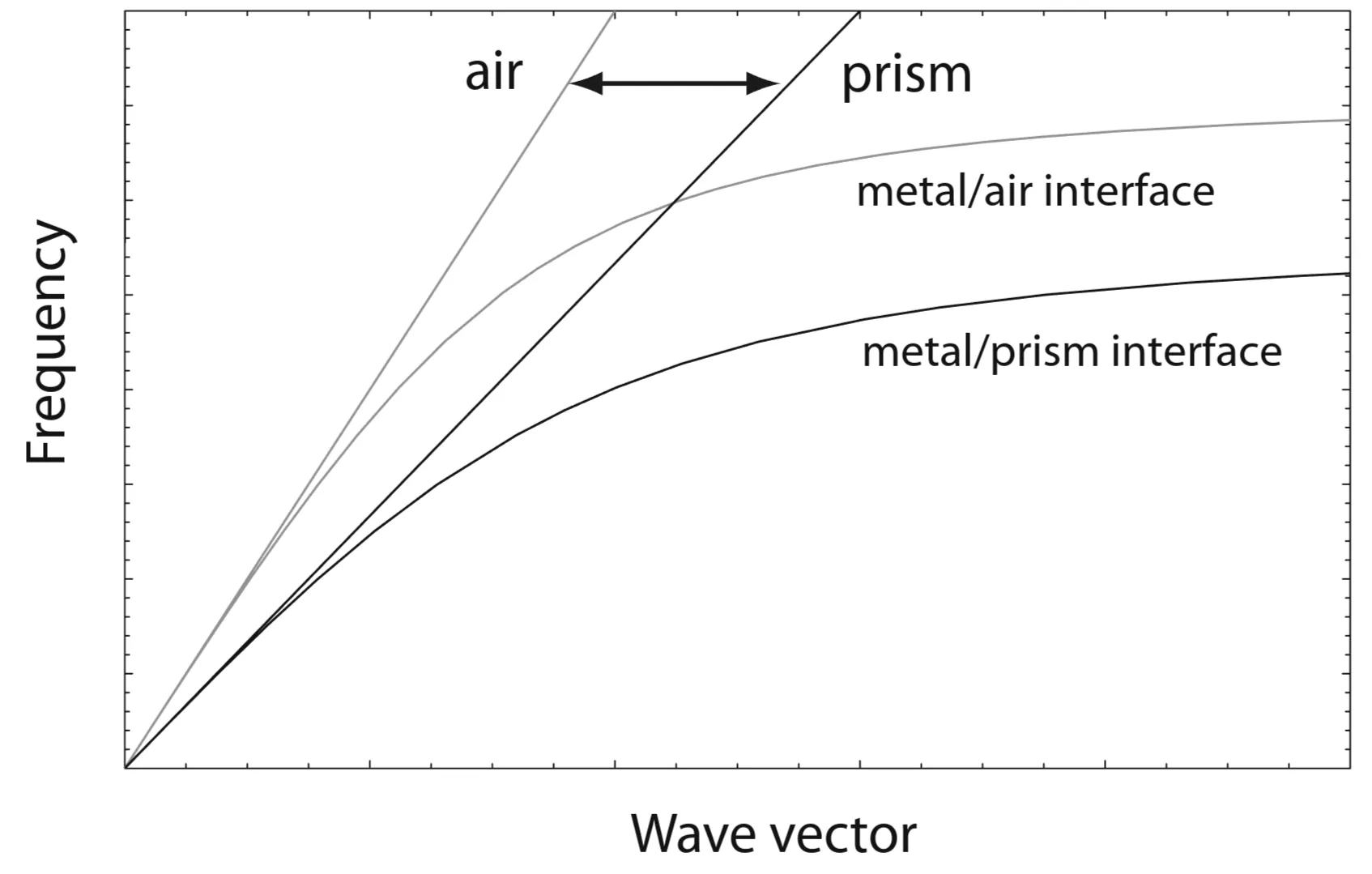
Direct illumination of a smooth metal/dielectric (for example metal/air) interface from the dielectric side cannot excite SPPs because the maximum in-plane momentum provided by the incident light, $k_x=k_0\sqrt{{\epsilon }_{\text{incident}}}\sin \theta$, is limited by $k_0\sqrt{{\epsilon }_{\text{incident}}}$ (at grazing incidence $\theta ={90}^{\circ }$), which is smaller than the SPP propagation constant $\beta$. However, phase-matching can be achieved by introducing a third medium with a higher refractive index, typically a prism, to increase the incident wave vector.

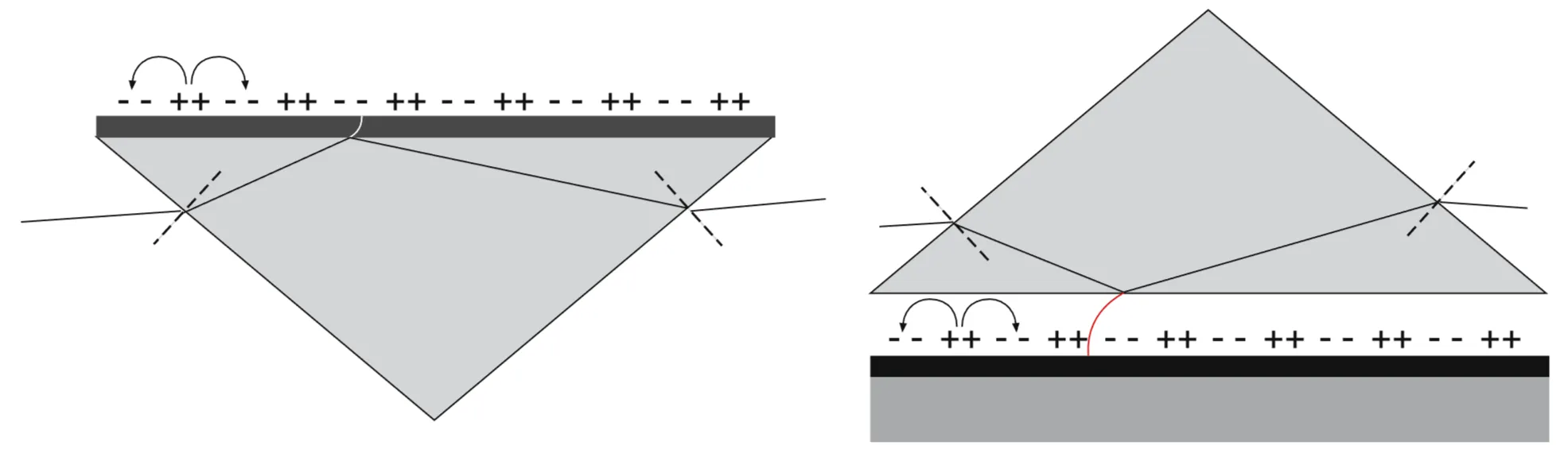
Consider a prism (material P, dielectric constant ${\epsilon }_P$) adjacent to a thin metal film (M, ${\epsilon }_M$), which is in contact with a lower-index dielectric (D, ${\epsilon }_D$, often air where ${\epsilon }_D\approx 1$). Light incident through the prism onto the prism/metal interface at an angle $\theta$ has an in-plane wave vector component $k_x=k_0\sqrt{{\epsilon }_P}\sin \theta$. If ${\epsilon }_P>{\epsilon }_D$, this $k_x$ can be made large enough to match the SPP propagation constant $\beta$ at the metal/dielectric (M/D) interface on the other side of the metal film. Two common configurations are:

This enhanced momentum $k_x$ can match ${\beta }_{\text{SPP}}$ for SPPs at the interface between the metal and the lower-index dielectric (D). This allows excitation of SPPs that propagate with $\beta$ values lying between the light lines of the lower-index dielectric (D) and the higher-index dielectric (prism, P). This excitation manifests as a minimum in the intensity of the light reflected from the prism base, a phenomenon known as Attenuated Total Reflection (ATR). The coupling involves the tunnelling of the evanescent fields (created by total internal reflection at the prism/metal interface if the metal is thin enough, or at the prism/gap interface in Otto) to the metal/dielectric (M/D) interface.

The two configurations shown are:

1. Kretschmann configuration (left): Light is incident through a prism onto a thin metal film deposited directly on the prism base. SPPs are excited at the outer metal/dielectric interface.
2. Otto configuration (right): Light is incident through a prism, which is separated from a bulk metal surface by a small gap filled with a low-index dielectric (typically air). SPPs are excited at the metal/gap interface.

Note that direct phase-matching to excite SPPs at the prism/metal (P/M) interface itself is generally not possible because the SPP dispersion curve for that interface (if it were to exist and be relevant) would typically lie outside the light cone of the prism material (so ${\beta }_{SPP,P/M}>k_0\sqrt{{\epsilon }_P}$), meaning no real angle $\theta$ could provide matching. The focus is on exciting SPPs at the M/D interface.

The figure illustrates how the SPP dispersion curve at the metal/air interface can be reached by the light line from the prism, while an SPP at a prism/metal interface would be inaccessible.

SPPs excited via prism coupling are inherently "leaky" if the metal film is thin enough (Kretschmann) or the gap is appropriate (Otto), meaning they can re-radiate energy back into the prism. The minimum in reflected intensity occurs due to destructive interference between the directly reflected light and this leakage radiation. An optimal metal film thickness (Kretschmann) or gap distance (Otto) can lead to near-zero reflection. This occurs under critical coupling, where the radiative damping rate (leakage back into the prism, ${\mathrm{\Gamma }}_{\text{rad}}$) equals the intrinsic damping rate of the SPP due to absorption in the metal (${\mathrm{\Gamma }}_{\text{abs}}$).
If ${\beta }_0$ is the complex propagation constant of the SPP at the M/D interface in the absence of the prism, ${\mathrm{\Gamma }}_{\text{abs}}=\mathrm{Im}\{{\beta }_0\}$. Critical coupling implies ${\mathrm{\Gamma }}_{\text{rad}}\approx \mathrm{Im}\{{\beta }_0\}$.

3.2 Grating Coupling

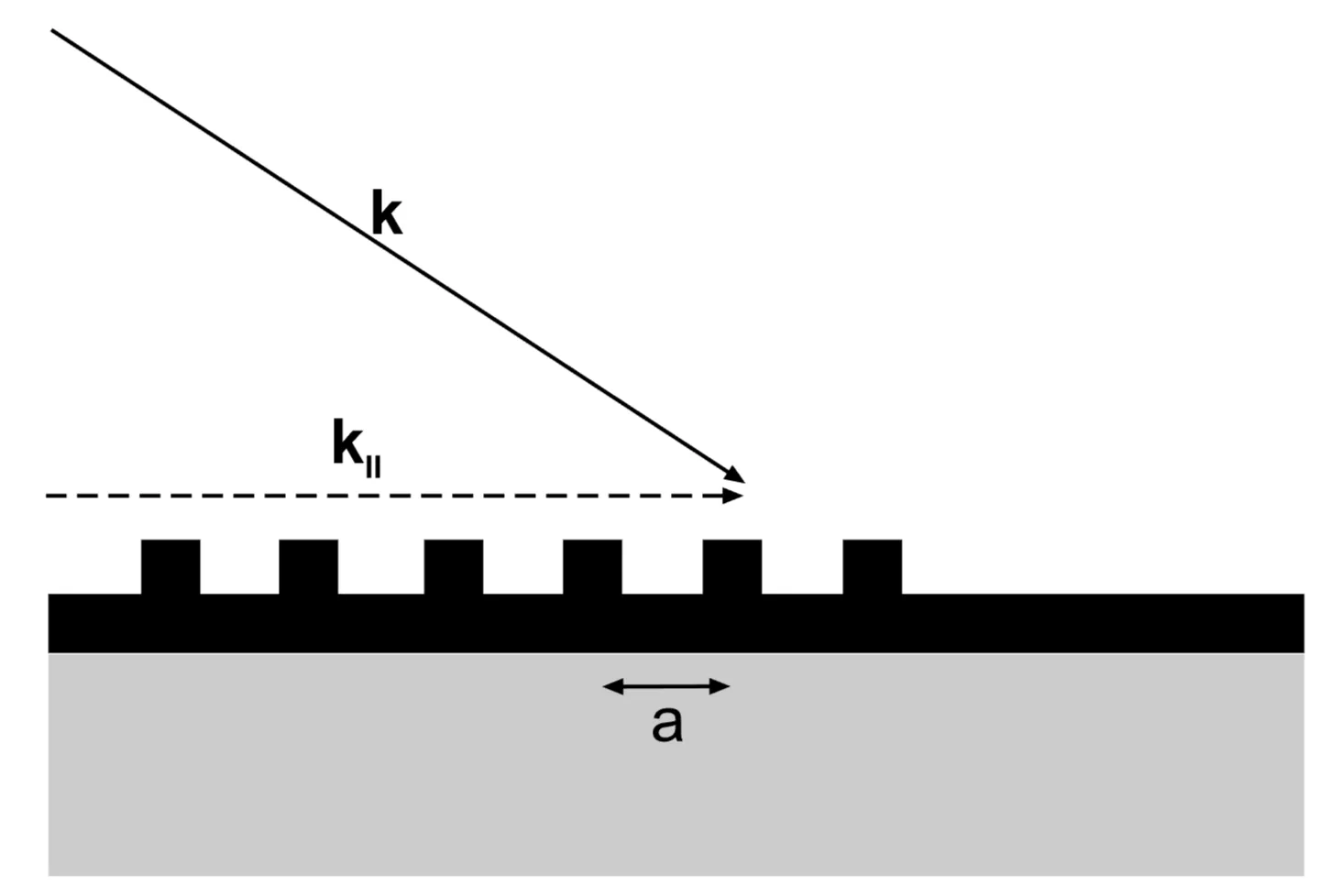
Phase-matching to excite SPPs can also be achieved by patterning the metal surface (or an adjacent dielectric surface) with a periodic structure, such as a grating of grooves or holes with a lattice constant $a$. For a simple one-dimensional grating, incident light with an in-plane wave vector component $k_x=k_0\sqrt{{\epsilon }_d}\sin \theta$ can couple to an SPP if its momentum is augmented by integer multiples of the grating vector $g=2\pi /a$. Phase-matching occurs when:

where $\nu =1,2,3,\dots$ is an integer representing the diffraction order. The excitation of SPPs is typically observed as a minimum in the reflectivity of the incident light at specific angles or wavelengths satisfying this condition.

The reverse process is also important: SPPs propagating along a periodically modulated surface can scatter and radiate into free-space light. By designing the grating geometry (shape, period, depth), the direction and polarisation of the out-coupled light can be controlled, and even focusing of light can be achieved.

More generally, SPPs can also be excited on metal films with random surface roughness or by using localized scatterers (like nanoparticles or defects). In these cases, the scatterers provide a broad range of momentum components $\mathrm{\Delta }{k}_x$. The phase-matching condition can be written as:

allowing for coupling over a wider range of incident angles and frequencies, albeit typically with lower efficiency than optimized periodic structures.

3.3 Excitation Using Highly Focused Optical Beams

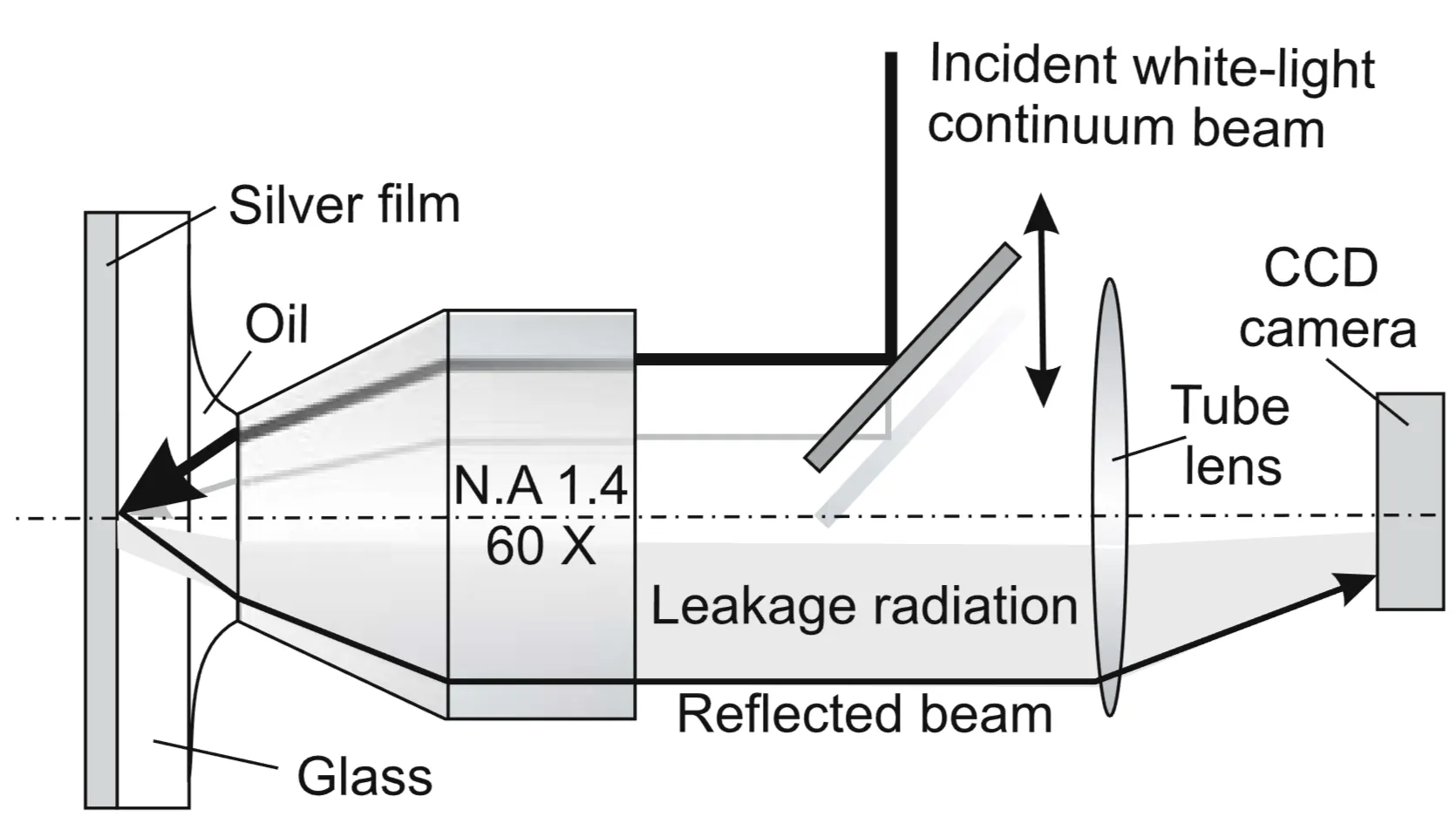
Another method to excite SPPs involves using a high numerical aperture (NA) microscope objective to tightly focus the incident light beam onto the metal surface, typically through a glass substrate (similar to an immersion lens scenario). A high NA objective produces a focused spot containing a broad angular spectrum of incident plane waves. Some of these plane waves will have angles of incidence $\theta$ (inside the glass, numerical aperture $n\sin \theta$) greater than the critical angle ${\theta }_c=\arcsin (\sqrt{{\epsilon }_{\text{air}}/{\epsilon }_{\text{glass}}})$ for total internal reflection at the glass/air interface (if the metal film is on the air side).

The evanescent fields generated by these components undergoing total internal reflection at the substrate/metal interface can provide the necessary momentum to phase-match SPPs at the outer metal/air interface. The in-plane wave vector available from the focused beam within the substrate (refractive index $n_{\text{sub}}$) is $k_x=n_{\text{sub}}{k}_0\sin \theta$. For SPP excitation at the metal/air interface, phase matching occurs for components at an angle ${\theta }_{\text{SPP}}$ such that:

Since $\beta >k_{0,\text{air}}$, this requires $n_{\text{sub}}\sin {\theta }_{\text{SPP}}>1$, meaning ${\theta }_{\text{SPP}}$ must be greater than the critical angle for the substrate/air interface (${\theta }_c=\arcsin (1/n_{\text{sub}})$).

The excited SPPs propagate along the metal/air interface and can subsequently leak radiation back into the substrate at this same angle ${\theta }_{\text{SPP}}$, due to the reciprocity of the coupling mechanism. This leakage radiation can be collected by the same objective. The images below illustrate the path of excited SPPs and their leakage radiation for p-polarised (TM) and s-polarised (TE) incident light.

As established in Chapter 2, SPPs are TM modes. Consequently, efficient excitation and subsequent leakage radiation are observed for p-polarised incident light, while s-polarised light does not couple to SPPs at a simple planar interface, resulting in no SPP trace in the corresponding image.