Jump back to chapter selection.

Table of Contents

5.1 Proof of Schottky's Theorem for Shot Noise
5.2 Modulation Instabilities
5.3 Autocorrelator
5.4 Diagnostics Measurements
5.5 Welch's Method to Obtain Power Spectral Density Estimates

5 Appendix

The purpose of this appendix is to offer additional context on certain topics that were considered too extensive to include in the main body of this thesis. Given that the primary focus of this thesis is experimental, theoretical aspects, including derivations and proofs, are provided here for completeness.

5.1 Proof of Schottky's Theorem for Shot Noise

Schottky's theorem is a fundamental result in electronics, stating that the shot noise power spectral density (PSD) is proportional to the average current.

Proof
While current flow appears continuous, the discrete nature of charge carriers (such as electrons) leads to random arrival times at the detector, which can be modelled as a Poisson process. The current arriving at the detector at any given time can be expressed as

I (t) = \sum_{j} e δ (t - t_{j}),

where $t_{j}$ represents the random arrival times of the charge carriers. The Wiener-Khinchin theorem connects the autocorrelation function of a signal to its PSD:

S_{x} (f) = 2 \int_{- \infty}^{\infty} R_{x} (τ) e^{- i 2 π f τ} d τ = 2 F {R_{x} (τ)} (f),

where the autocorrelation function is defined as

R_{x} (τ) = lim_{T \to \infty} \frac{1}{T} \int_{- T / 2}^{T / 2} x (t) x (t + τ) d t .

Applying this to the problem, with $x (t) = I (t)$ , we have

\begin{aligned} R_{shot} (τ) & = lim_{T \to \infty} \frac{1}{T} \int_{- T / 2}^{T / 2} I (t) I (t + τ) d t \\ = lim_{T \to \infty} \frac{e^{2}}{T} \sum_{j} \sum_{k} \int_{- T / 2}^{T / 2} δ (t - t_{j}) δ (t - t_{k} + τ) d t . \end{aligned}

Evaluating the integral:

\int_{- T / 2}^{T / 2} δ (t - t_{j}) δ (t - t_{k} + τ) d t = {\begin{cases} δ (t_{j} - t_{k} + τ), & if - T / 2 < t_{j} < T / 2 \\ 0, & otherwise \end{cases}

This leads to

R_{shot} (τ) = lim_{T \to \infty} \frac{e^{2}}{T} \sum_{\begin{matrix} j \\ - T / 2 < t_{j} < T / 2 \end{matrix}} \sum_{k} δ (t_{j} - t_{k} + τ) .

Care must be taken when evaluating this expression. For $j = k$ , the times match, and we obtain $δ (τ)$ . Assuming there are $N$ terms for which the time constraint is satisfied, this yields a contribution of $N δ (τ)$ . For $j \neq k$ , the delta functions are randomly distributed, and with appropriate averaging, their contributions to the autocorrelation function cancel out. It is important to note, however, that this "appropriate averaging" is a non-trivial process, and therefore, it will not be elaborated upon here.

Thus, we are left with

R_{shot} (τ) = N \frac{e^{2}}{T} δ (τ) = e \bar{I} δ (τ),

where $\bar{I}$ is the average current, defined as the number of charges per unit time. The PSD is then obtained as

S_{shot} (f) = 2 F {e \bar{I} δ (τ)} (f) = 2 e \bar{I} .

This concludes the proof.

It is worth noting that this result holds even if the current pulses are not modelled as delta functions but as square pulses. If the pulses have a duration $τ_{p u l s e}$ , the resulting PSD is given by (without proof)

S_{shot} (f) = 2 e \bar{I} {(\frac{\sin (π f τ_{p u l s e})}{π f τ_{p u l s e}})}^{2} .

While this expression differs from the earlier result, it is important to consider that $τ_{p u l s e}$ is the mean transit time of electrons, typically on the order of $10 ps$ . Therefore, the cut-off frequency is $f = 1 / τ_{p u l s e} \approx 100 GHz$ , meaning that the assumption of shot noise being white noise is valid for most practical circuits.

5.2 Modulation Instabilities

To begin the discussion, it is essential to recognise that the nonlinear coefficient, $γ$ , is generally frequency-dependent, that is, $γ = γ (ω)$ . Additionally, approximating the dispersion as a polynomial truncated at the second order may not always be sufficient. This section closely follows established derivations and discussions, for instance, those found in seminal texts on nonlinear fibre optics. Therefore, we start with a generalised form of the Nonlinear Schrödinger Equation (NLSE):

\frac{\partial \tilde{A} (ω - ω_{0})}{\partial z} + i (k (ω) - k (ω_{0}) - \frac{ω - ω_{0}}{v_{g} (ω_{0})}) \tilde{A} (ω - ω_{0}) = - i γ (ω) F {| A |^{2} A},

where $v_{g}$ is the group velocity, and $ω_{0}$ represents the centre or envelope frequency of a pulse. Let $Ω = ω - ω_{0}$ . To ensure consistency in the NLSE presented above, note that the term in brackets, $k (ω) - k (ω_{0}) - \frac{ω - ω_{0}}{v_{g} (ω_{0})}$ , can be expanded using a Taylor series of $k (ω)$ around $ω_{0}$ . Given that $k^{'} (ω_{0}) = 1 / v_{g} (ω_{0})$ , this term simplifies to $\frac{k^{″} (ω_{0})}{2} Ω^{2} + \frac{k^{‴} (ω_{0})}{6} Ω^{3} + \dots$ .

Consider a continuous wave (CW) centred around $ω_{0}$ :

\frac{\partial {\tilde{A}}_{cw}}{\partial z} = - i γ (ω_{0}) F {| A_{cw} |^{2} A_{cw}} = - i γ (ω_{0}) P_{0} A_{cw},

where the field normalisation ensures that the absolute square of the amplitude represents the power in the fibre. This leads to a nonlinear phase shift:

{\tilde{A}}_{cw} (z) = {\tilde{A}}_{cw} (z = 0) e^{- i γ (ω_{0}) P_{0} z} .

Next, we express the electric field as a perturbation:

A (z, t) = [A_{cw} + a (z, t)] e^{- i γ (ω_{0}) P_{0} z},

where the perturbation $a (z, t)$ is small, allowing us to neglect second and higher-order terms. Substituting this into the $| A |^{2} A$ term in the NLSE gives:

| A |^{2} A \approx (| A_{cw} |^{2} A_{cw} + 2 | A_{cw} |^{2} a + A_{cw}^{2} a^{*}) e^{- i γ (ω_{0}) P_{0} z} .

Thus, the NLSE for the perturbation $\tilde{a} (Ω)$ becomes:

- i γ (ω_{0}) | A_{cw} |^{2} \tilde{a} (Ω) + \frac{\partial \tilde{a} (Ω)}{\partial z} + i K (Ω) \tilde{a} (Ω) = - i γ (ω_{0} + Ω) [2 | A_{cw} |^{2} \tilde{a} (Ω) + A_{cw}^{2} {\tilde{a}}^{*} (- Ω)],

where the dispersion term is defined as:

K (Ω) = k (ω_{0} + Ω) - k (ω_{0}) - \frac{Ω}{v_{g} (ω_{0})} = \sum_{m = 2}^{\infty} \frac{k^{(m)} (ω_{0})}{m!} Ω^{m} .

If $γ (ω)$ is frequency-independent (i.e. $γ (ω) = γ_{0}$ ), we obtain a matrix equation by considering the equations for $\tilde{a} (Ω)$ and ${\tilde{a}}^{*} (- Ω)$ :

\frac{\partial}{\partial z} [\begin{matrix} \tilde{a} (Ω) \\ {\tilde{a}}^{*} (- Ω) \end{matrix}] = i [\begin{matrix} - K (Ω) - γ_{0} P_{0} & γ_{0} P_{0} \\ γ_{0} P_{0} & K (- Ω) + γ_{0} P_{0} \end{matrix}] [\begin{matrix} \tilde{a} (Ω) \\ {\tilde{a}}^{*} (- Ω) \end{matrix}] .

The eigenvalues of the resulting coupling matrix indicate the gain for spectral sidebands at frequency shifts of $\pm Ω$ :

λ_{\pm} = \frac{i}{2} (K (- Ω) - K (Ω) \pm \sqrt{(K (- Ω) + K (Ω))} \sqrt{(K (- Ω) + K (Ω)) + 4 γ_{0} P_{0}}),

which reduces to:

λ_{\pm}^{standard} = \frac{i}{2} (\pm \sqrt{β_{2} Ω^{2}} \sqrt{β_{2} Ω^{2} + 4 γ_{0} P_{0}})

in the standard case where only second-order dispersion is considered, $K (Ω) \approx \frac{β_{2}}{2} Ω^{2}$ , so $K (Ω) + K (- Ω) \approx β_{2} Ω^{2}$ (assuming $β_{2} = k^{″} (ω_{0})$ is real and other even order dispersion terms are negligible). For negative group velocity dispersion (GVD) $(β_{2} < 0)$ , the term under the square root can become negative, leading to real $λ$ and thus gain, until the frequency shift $Ω$ reaches a sufficient value. The gain and loss parts of the eigenvalues depend on $K (Ω) + K (- Ω)$ , which involves only even orders of dispersion.

By defining $Δ k (Ω) = K (- Ω) + K (Ω) = k (ω_{0} - Ω) + k (ω_{0} + Ω) - 2 k (ω_{0})$ , we express the gain eigenvalues (where $λ$ is real) as:

λ_{\pm}^{gain} = \pm \frac{1}{2} \sqrt{- Δ k (Ω) (Δ k (Ω) + 4 γ_{0} P_{0})} .

The parameter $γ_{0} P_{0}$ is associated with the CW intensity, indicating the presence or absence of modulation instability gain at different frequencies. As shown in the next figure, the behaviour of the modulation instabilities is characterised by the wavenumber shift and the corresponding power gain across different optical frequencies. The figure illustrates how the instabilities predominantly exhibit significant gain far from the central optical frequency of the laser, indicating that these instabilities are not relevant in the frequency range of interest.

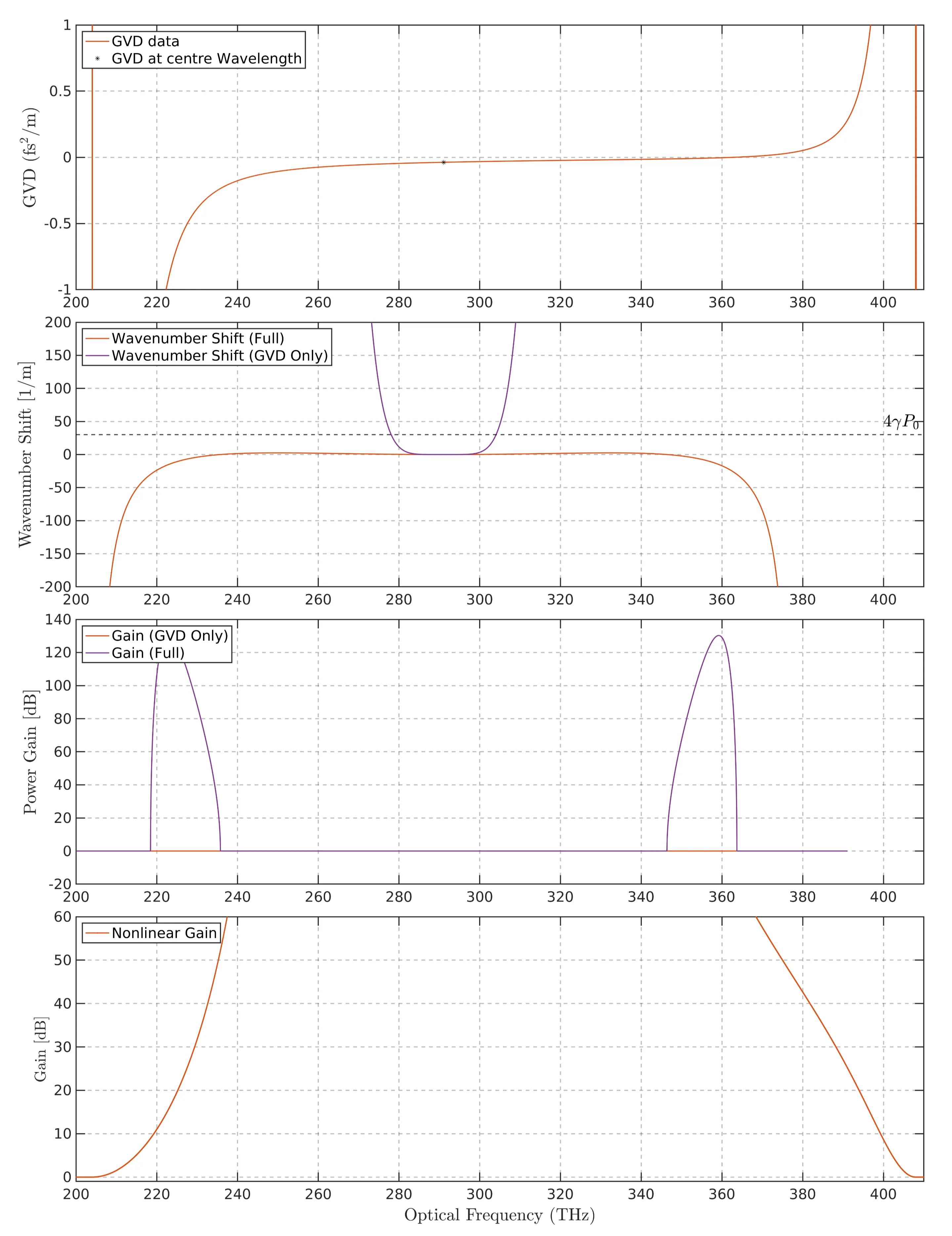
Attachments/Koeberlin_Master_Thesis 46.webp|700
Overview of modulation instabilities in the fibre. (a) The group velocity dispersion (GVD) data shows the raw GVD values across different optical frequencies, with a marker at the centre wavelength highlighting the GVD used in calculations. (b) Wavenumber shift as a function of optical frequency, comparing the full model and the model considering only the GVD contribution. The horizontal dashed line represents the constant term $4 γ P_{0}$ . (c) Power gain in dB for the cases considering only GVD and the full model, showing significant differences away from the centre frequency. (d) Nonlinear gain across optical frequencies, illustrating the gain behaviour influenced by nonlinear effects. The x-axis is shared among all subplots, representing optical frequency in THz.

5.3 Autocorrelator

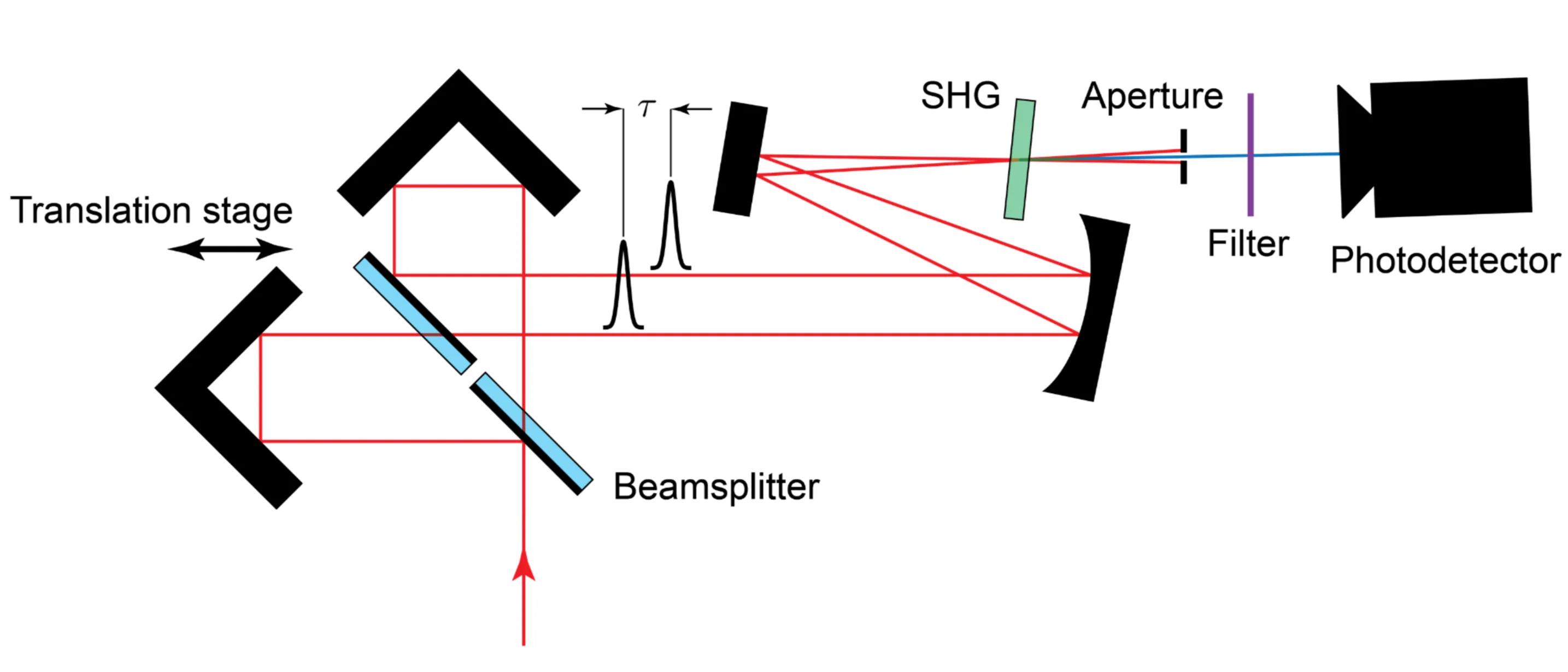
As pulse durations become shorter than $1 ps$ , which is beyond the electronic time resolution, measuring pulse width using purely electronic means becomes increasingly difficult. A widely used method for characterising ultrashort pulses is intensity autocorrelation, which employs second harmonic generation (SHG), as depicted in the next figure. The following description closely follows established explanations found in literature on ultrashort pulses.

Attachments/Koeberlin_Master_Thesis 47.webp|700

In this method, a beamsplitter divides the incident laser beam into two beams of identical intensity. One of the beam paths is delayed relative to the other by a time $τ$ . Both beams are then focused into a nonlinear crystal where they overlap in both space and time. Due to the nonlinear properties of the crystal, SHG occurs, generating a signal at twice the frequency of the original beam ( $2 ω$ ). The intensity of this SHG signal depends on the time delay $τ$ between the two pulses.

It can be shown that the SHG signal is minimal when the pulses do not overlap temporally and reaches a maximum when they are perfectly overlapped in time. Due to momentum conservation and the non-collinear configuration of the incident beams, the frequency-doubled signal appears spatially between the two original beams. An aperture can be used to isolate and measure only the SHG signal's intensity:

I_{2 ω} (τ) \sim \int_{- \infty}^{\infty} | E (t) E (t + τ) |^{2} d t = \int_{- \infty}^{\infty} I (t) I (t + τ) d t .

Since this intensity is symmetric with respect to the delay, that is, $I_{2 ω} (τ) = I_{2 ω} (- τ)$ , the autocorrelation measurement cannot reveal asymmetries in the pulse. To accurately extract the pulse duration, an assumption about the pulse shape is required, as the autocorrelation trace alone does not provide detailed information about the pulse's shape or structure.

5.4 Diagnostics Measurements

This section presents various measurements from the optical spectrum analyser (OSA), microwave spectrum analyser (MSA), and autocorrelator for completeness. The results are shown in Figures 4.3 to 4.5.

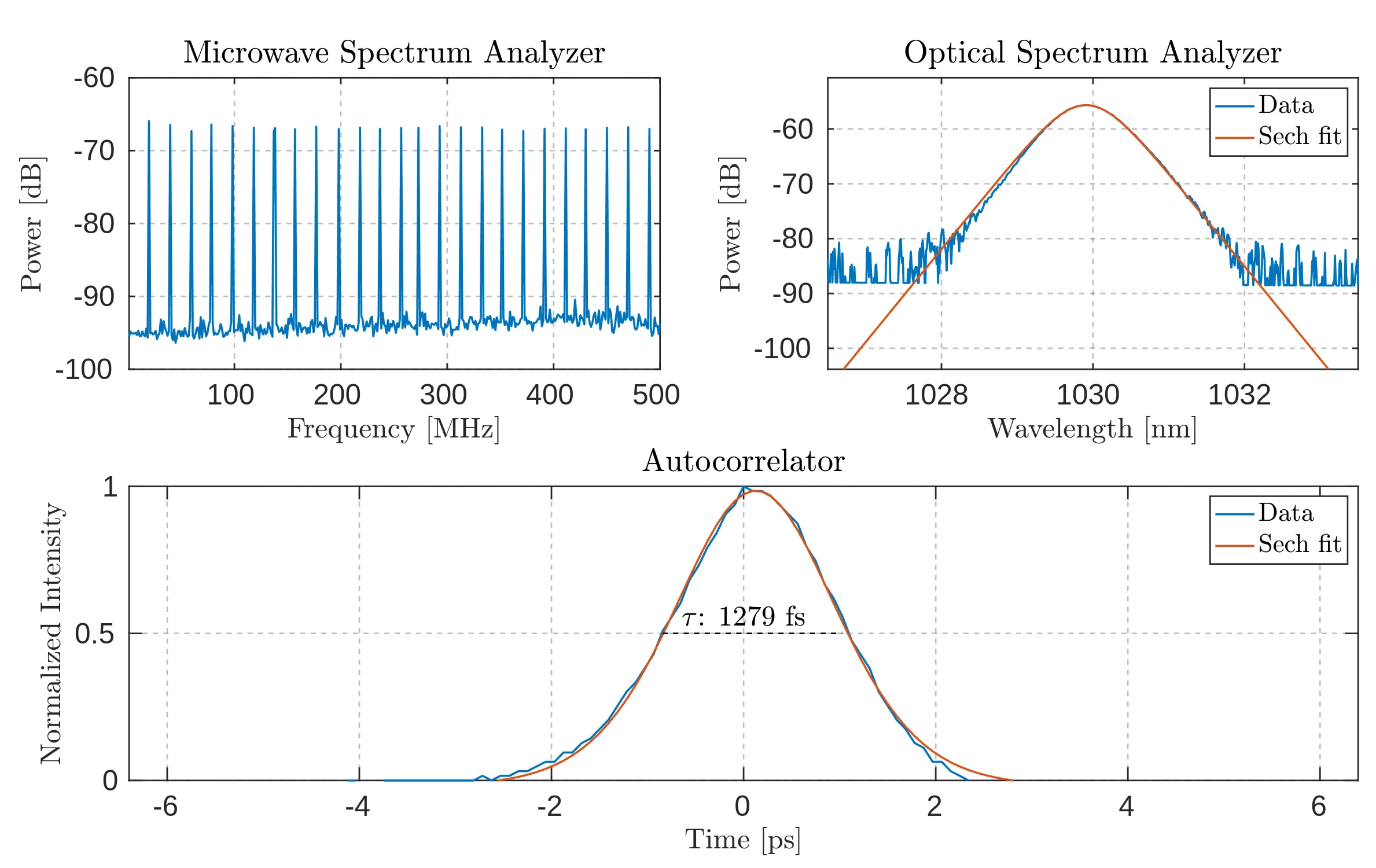
Attachments/Koeberlin_Master_Thesis 48.webp|700
Combined diagnostic results from the microwave spectrum analyser (MSA) with a resolution bandwidth of $3 kHz$ , autocorrelator, and optical spectrum analyser (OSA). The red line indicates an ideal soliton pulse fit. Measurement performed at $173 W$ pump power.

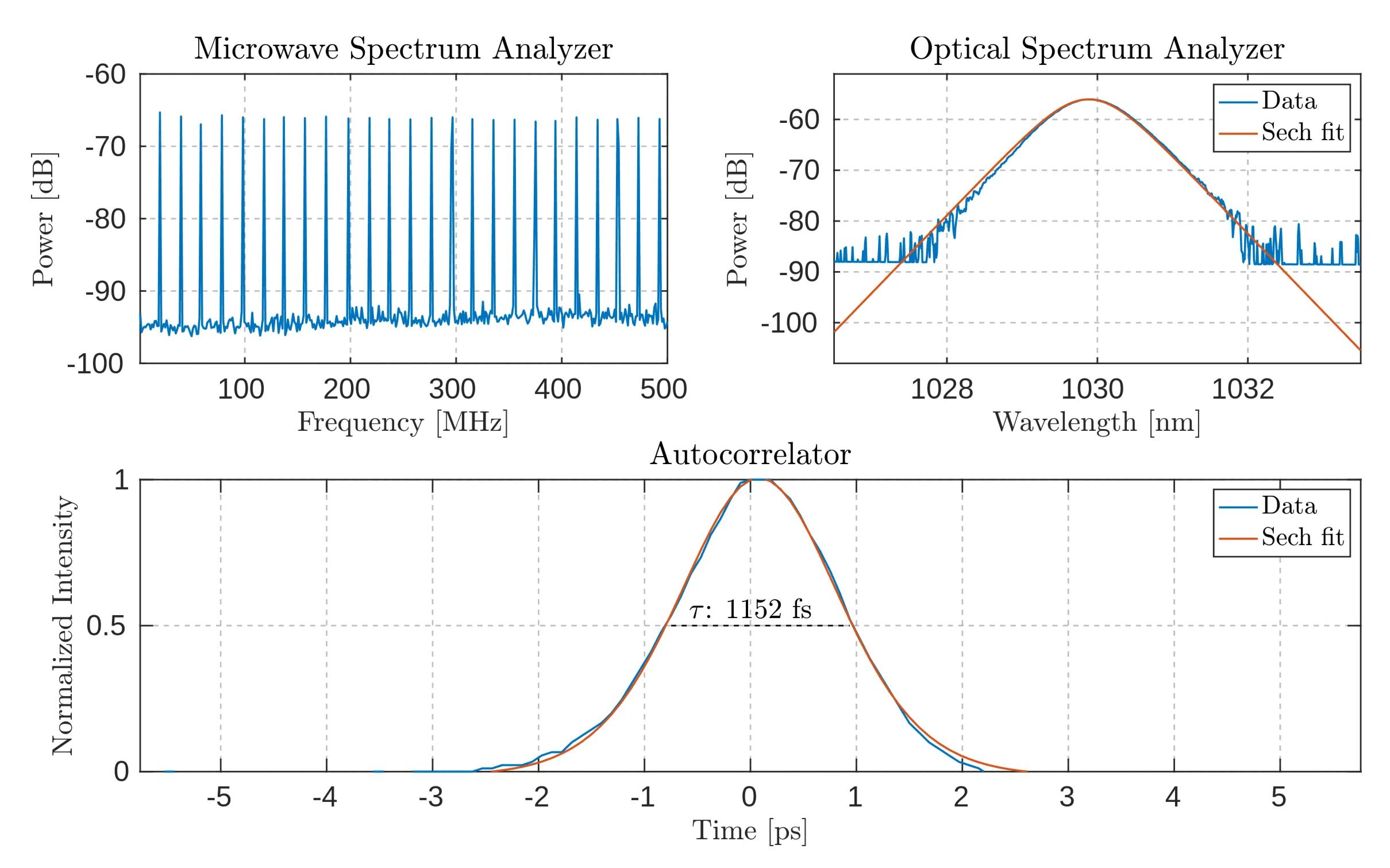
Attachments/Koeberlin_Master_Thesis 49.webp|700
Combined diagnostic results from the microwave spectrum analyser (MSA) with a resolution bandwidth of $3 kHz$ , autocorrelator, and optical spectrum analyser (OSA). The red line indicates an ideal soliton pulse fit. Measurement performed at $191 W$ pump power.

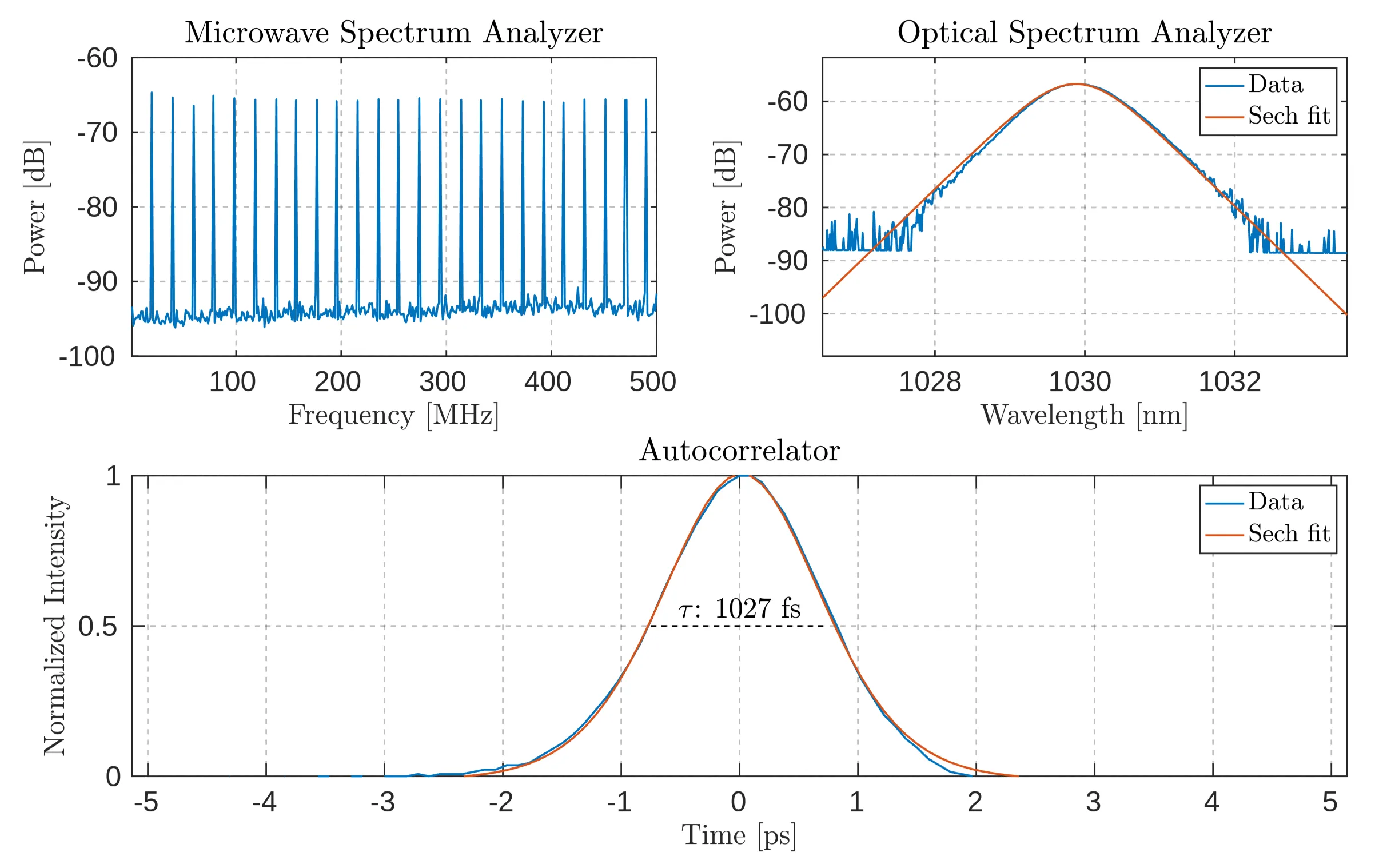
Attachments/Koeberlin_Master_Thesis 50.webp|700
Combined diagnostic results from the microwave spectrum analyser (MSA) with a resolution bandwidth of $3 kHz$ , autocorrelator, and optical spectrum analyser (OSA). The red line indicates an ideal soliton pulse fit. Measurement performed at $214 W$ pump power.

5.5 Welch's Method to Obtain Power Spectral Density Estimates

As described in Section 3.5.3, Welch's method was employed to smooth the noise PSD data and provide visual clarity. Welch's method is a widely-used approach for estimating the power spectral density of a signal. Unlike a basic periodogram, which can be noisy and less reliable due to its high variance, Welch's method provides a smoother and more reliable estimate by averaging multiple periodograms of overlapping data segments. The initial noise in the data results from the fact that the experiment was conducted with a finite sampling rate and over a finite measurement time. If both the sampling rate and time were infinite, the resulting curve would appear smooth, as the non-stationary signal components would diminish. The process of Welch's method can be broken down into the following steps:

The signal is divided into 100 overlapping segments, with an $80 %$ overlap used between successive segments. Overlapping reduces information loss at the segment boundaries and provides more samples for averaging.
A window function, in this case a Hann window, is applied to each segment to minimise spectral leakage. This reduces spectral leakage by avoiding sharp discontinuities at the segment boundaries.
For each windowed segment, the Fast Fourier Transform (FFT) is used to compute the periodogram, which provides the PSD estimate for that segment.
Finally, the periodograms of all segments are averaged to produce the overall PSD estimate, reducing variance and creating a smoother representation of the spectral density.

The main strength of Welch's method lies in its ability to reduce the variance of PSD estimates. Compared to a single periodogram, Welch's method is much less sensitive to fluctuations in the data, offering a more stable and reliable representation of the signal's frequency content. In this thesis, it was employed to reveal the shot-noise limit and distinguish the signal from noise in the high-power laser system. However, the primary trade-off is a reduction in frequency resolution. Additionally, Welch's method increases the computational load, as the FFT must be applied multiple times across the overlapping segments.