Jump back to chapter selection.

Table of Contents

3.1 Oscillator
3.2 Beam Diagnostics
3.3 Fibre Coupling
3.4 Grating Spectrometer
3.5 Characterisation
3.6 Technical Considerations
3.7 Full Setup

3 Setup, Characterisation and Results

This chapter discusses the thesis's experimental setup, including the design of the oscillator, fibre coupling, grating spectrometer, and noise measurement techniques. The steps are discussed in the order of the beam path, starting from the laser cavity and ending in the detection setup.

3.1 Oscillator

The cavity design employs a two-pass geometry to achieve a repetition frequency of $19.7\text{ MHz}$, a pulse duration of $1030\text{ fs}$, and an average output power of $60\text{ W}$. This two-pass configuration balances maximising the gain per roundtrip and maintaining a manageable system complexity, as each additional pass requires two more mirrors, which can quickly crowd the oscillator setup.

The choice of repetition rate is crucial and not arbitrary. A higher repetition rate allows for noise measurements to extend to higher frequencies but also results in lower pulse energies and peak powers, which is not ideal for achieving significant spectral broadening. Conversely, a lower repetition rate enhances spectral broadening due to the increased pulse energies and peak powers; however, it limits noise measurements by restricting the maximum frequency components that can be effectively measured. Thus, a repetition rate of about $20\text{ MHz}$ offers a reasonable compromise between these competing factors.

The repetition frequency is determined by the distance from the output coupler to the end mirror, $l=\frac{c}{2f_{\text{rep}}}=7.6\text{ metres}$, where the factor of two accounts for the light being outcoupled only once per full roundtrip. The average output power is indirectly controlled, as the gain medium is assumed to be fixed. The output power relates to the intracavity power by $P_{\text{intra}}=\frac{P_{\text{avg}}}{r}$, where $r$ is the output coupling rate, influencing the fluence on the end mirror or saturable absorber, in this case, a SESAM. A bare two-pass cavity, symmetric in the beam waist as a function of position, serves as the starting point. The next figure shows this configuration with two passes on the disk, an output coupler, and an end mirror.

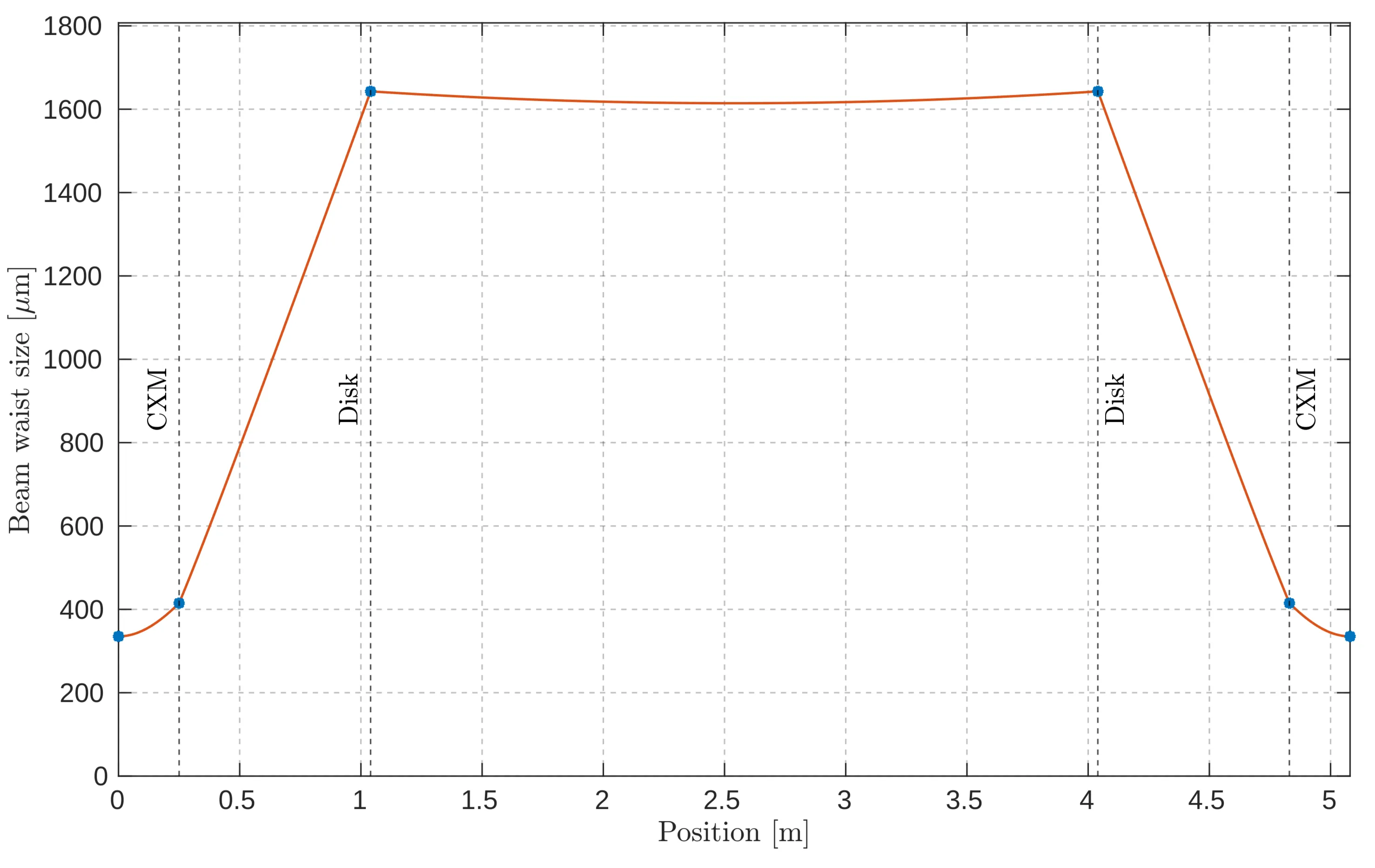
Evolution of the beam waist size (orange) within the simplest two-pass cavity in a symmetric configuration. The black dashed vertical lines and blue dots denote curved mirrors or the disk, with a nominal radius of curvature of $-2\text{ m}$. The beam size exhibits a symmetric pattern, repeating approximately every $2.5\text{ metres}$. This configuration serves as the starting point for optimising the final cavity design.

From this starting point, parameters such as distances between mirrors are adjusted, and additional mirrors are added to fit our needs. For stability, the beam must always focus at the ends of the cavity to maintain the periodicity of the beam waist.

To achieve soliton mode-locking, sufficient self-phase modulation is needed to counteract the group delay dispersion. The B-integral quantifies the SPM:

There is no additional SPM medium in the cavity, which is unique compared to most low-power, non-thin-disk lasers that achieve significant self-phase modulation (SPM) within the gain medium, as SPM through air propagation is negligible. In contrast, high-power TDLs usually require a vacuum to reduce undesirable SPM effects. For stable mode-locking, a B-integral around $50\text{ mrad}$ is typically required, based on empirical results.

The next figure shows the final configuration of the TDL cavity, featuring a telescope to control the beam size on the SESAM and, consequently, the fluence on the SESAM. Group Delay Dispersion is introduced using Gires-Tournois interferometer style (GTI) mirrors. These mirrors, while often named after the classical GTI with an air gap, are chirped mirrors. They achieve the desired wavelength-dependent phase shift through a carefully designed, wavelength-dependent optical path difference.

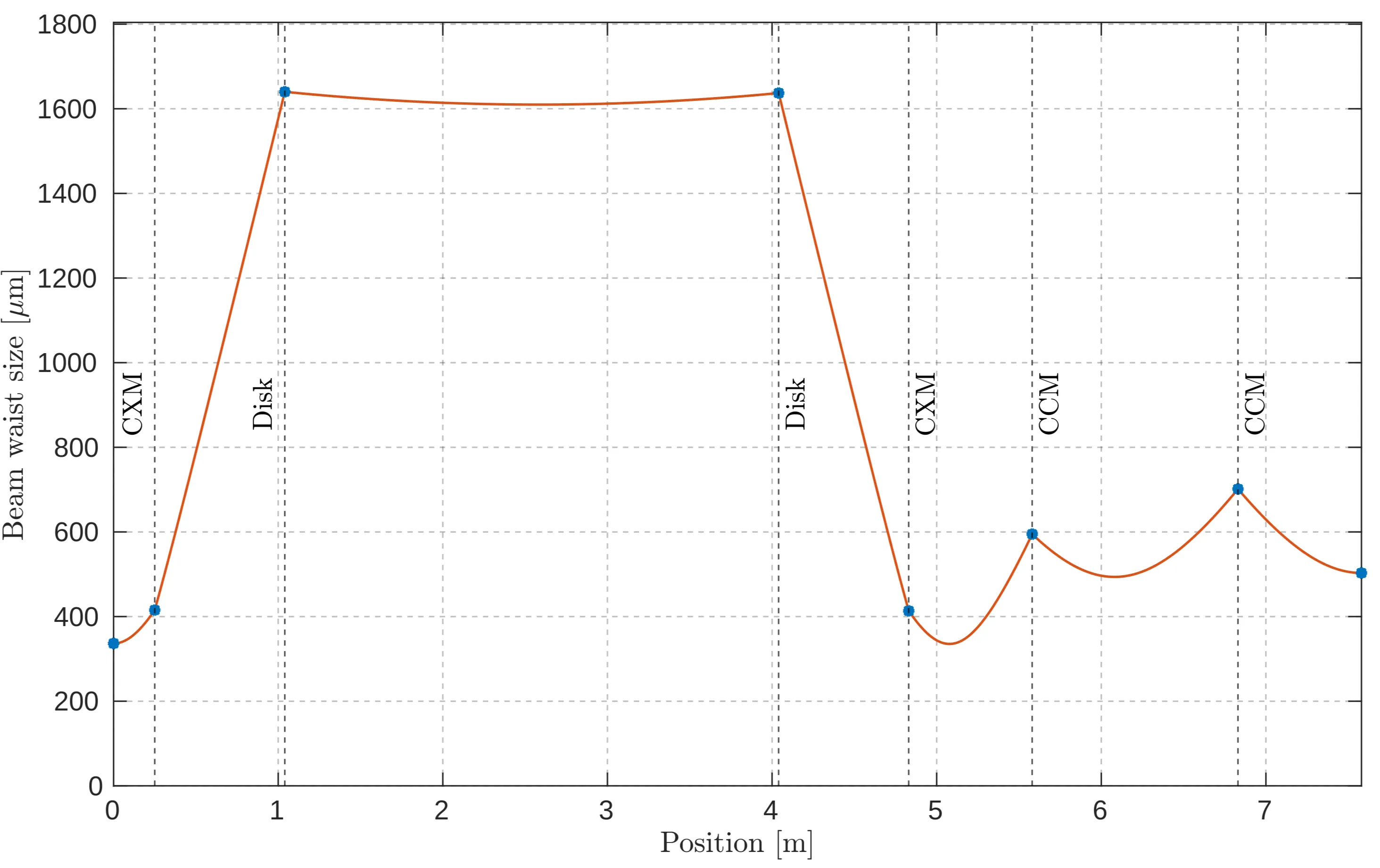
Beam waist evolution in the final cavity configuration, illustrating the change in beam waist size as the light travels through the cavity, starting from the output coupler and ending at the SESAM. Curved mirrors, the TDL disk, SESAM and OC are depicted with blue dots. Plane mirrors and plane GTIs are not shown.

Long-term stability in high-power oscillators also necessitates careful management of thermal effects, as increased power enhances both thermal lensing and disk bending. These effects result in a temperature-dependent radius of curvature, influenced by heating and gas convection in front of the disk. Thermal lensing and gas convection effects are equally significant in an air-filled cavity. The cavity must operate in a regime where small variations in the disk's curvature do not lead to destabilisation. As shown in the next figure, no nearby singularities indicate a stable configuration:

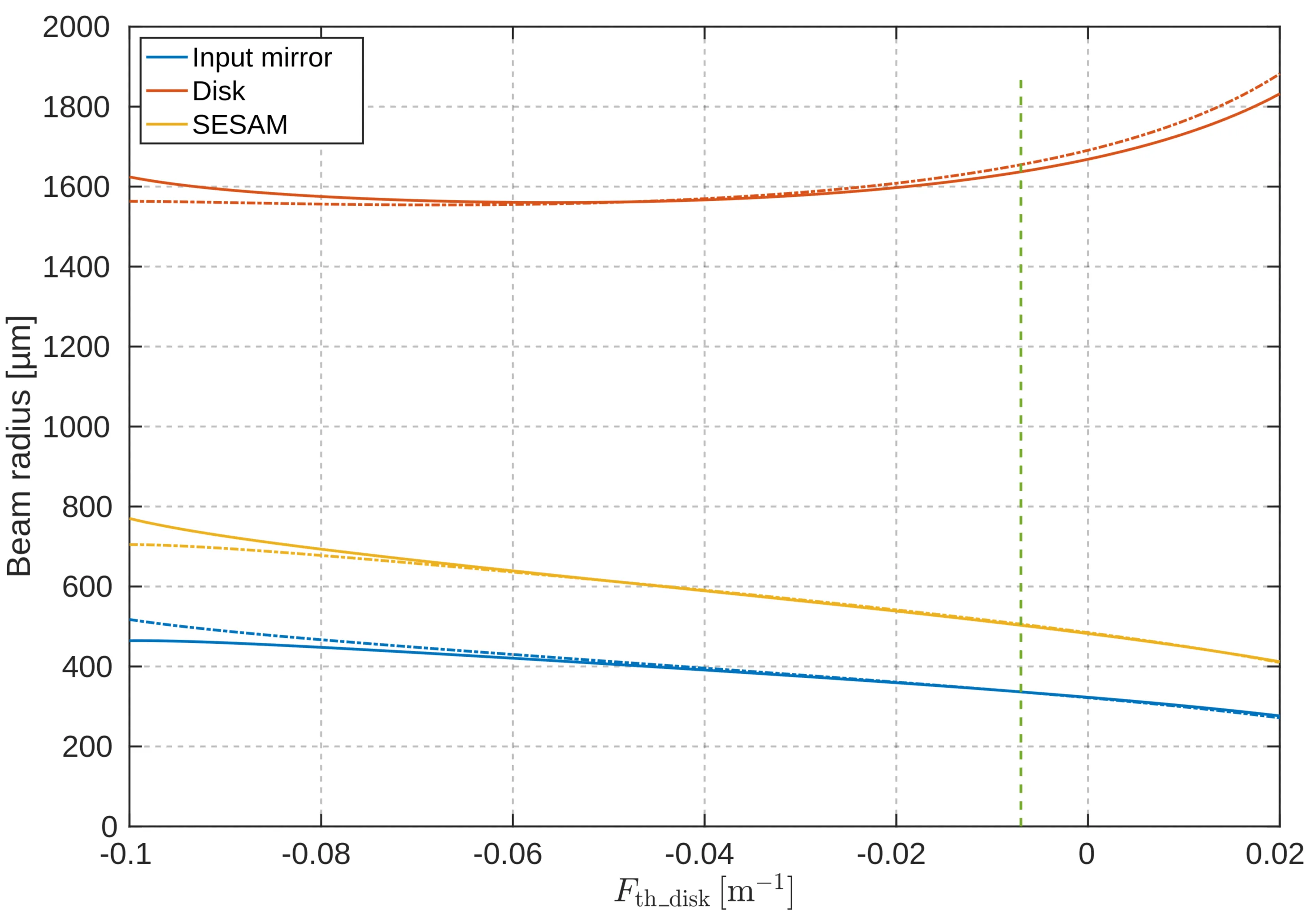
Beam radius on the SESAM as a function of its thermal lensing. The horizontal axis covers a very broad range, fully encompassing the laser's operating range. The absence of singularities or rapid changes suggests a stable configuration with respect to thermal lensing. The operation point of the cavity is depicted as a dashed line.

The following schematically depicts the final cavity configuration. To control the polarisation of the laser output, a thin-film polariser is introduced into the cavity. This ensures that only light with a well-defined polarisation can oscillate, improving the overall beam quality and stability of the cavity.

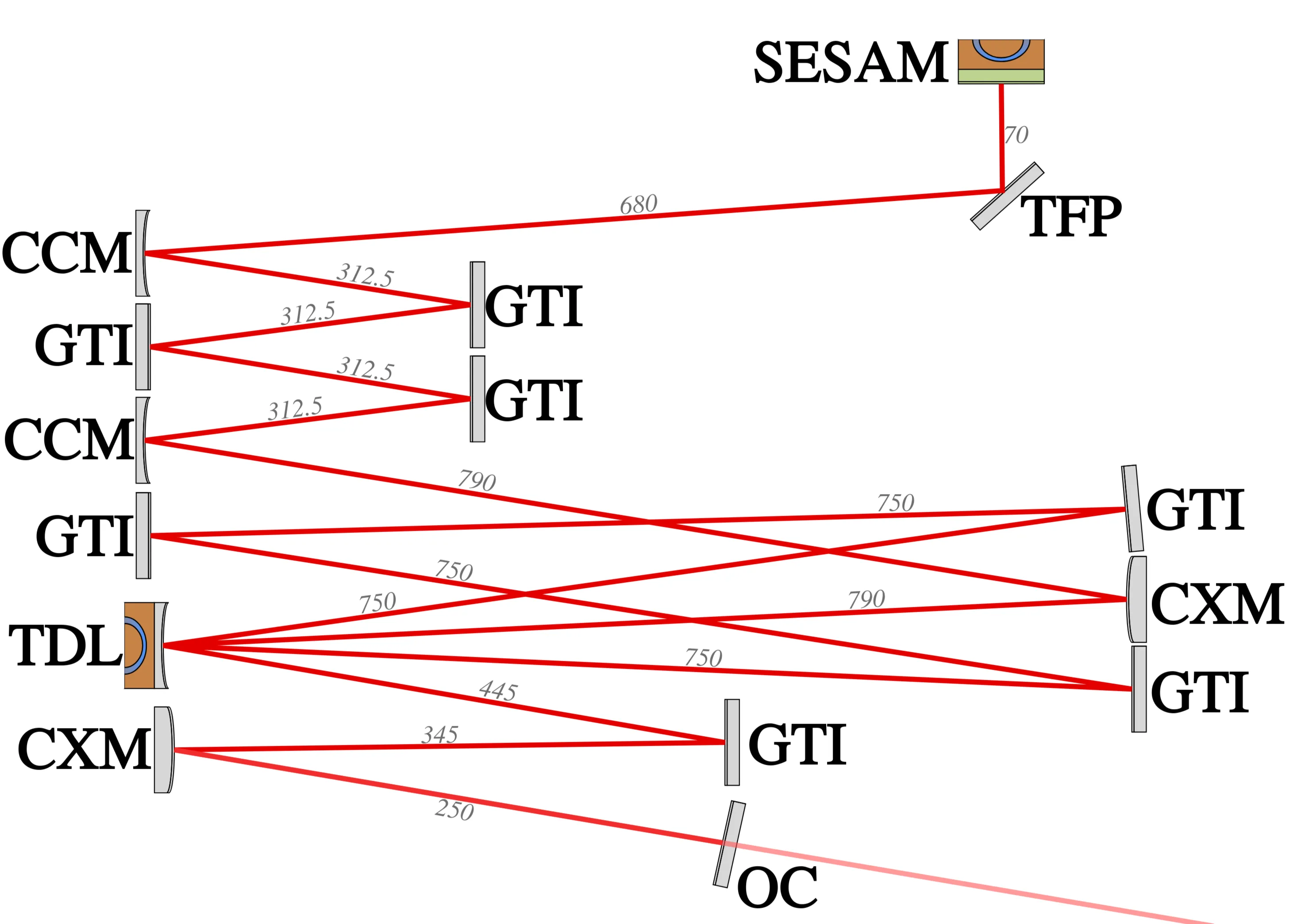
Schematic of the laser cavity and its components. GTI denotes the Gires-Tournois interferometer, TFP represents the thin-film polariser, OC is the output coupler, CCM is the concave mirror, CXM is the convex mirror, and TDL stands for the thin-disk laser. The blue elements behind the SESAM and TDL indicate active water cooling. The path of the oscillating light is shown schematically, with distances in millimetres marked in grey.

The efficiency of the laser system is crucial for evaluating its performance. The output power $P_{\text{output}}$ is related to the pump power $P_{\text{pump}}$ by the following equation:

where $P_{\text{threshold}}$ is the laser's threshold power, and $\eta$ represents the slope efficiency. This key figure of merit approaches $38\mathrm{\%}$ at high pump powers. The next figure illustrates the output power and slope efficiency as a function of the pump power:

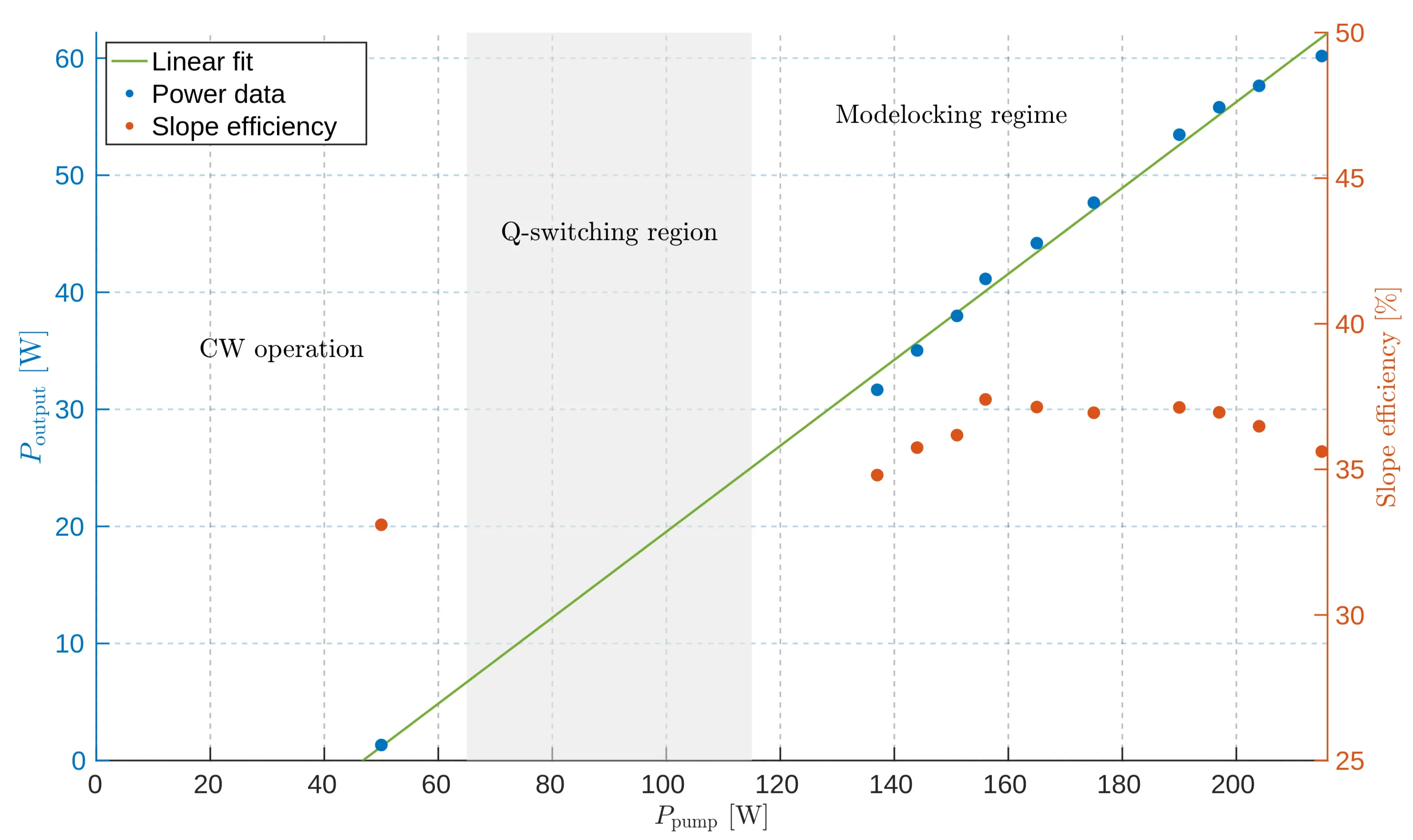
Output power (left) and slope efficiency (right) of the thin-disk laser as a function of pump power. The first data point is before mode-locking has been achieved, while the grey-shaded area is the Q-switching regime ($65\text{ to }115\text{ W}$). Therefore, no data has been recorded here.

The next table shows the parameters of this laser cavity.

3.2 Beam Diagnostics

3.2.1 $M^2$ Measurement

After the laser light exits the cavity, it is crucial to characterise the output beam quality. A small fraction of the laser power is extracted and directed towards the diagnostics setup. The key metric for beam quality is the $M^2$ value, which quantifies how closely the laser beam approximates an ideal Gaussian beam. An ideal Gaussian beam has an $M^2$ value of 1, indicating minimal divergence and optimal focusability. A higher $M^2$ value indicates greater beam divergence and reduced focusability. The relationship between the beam divergence angle $\theta$, the beam waist $w_0$, and the $M^2$ value is given by:

The next figure presents the results of the $M^2$ measurement, yielding a value of $M^2<1.1$. This measurement was conducted by passing the laser beam through a focusing lens, after which a moving stage equipped with a slit profiler measured the beam width along the $X$ and $Y$ axes at various positions along the beam path. The collected data points were then fitted to calculate the $M^2$ value.

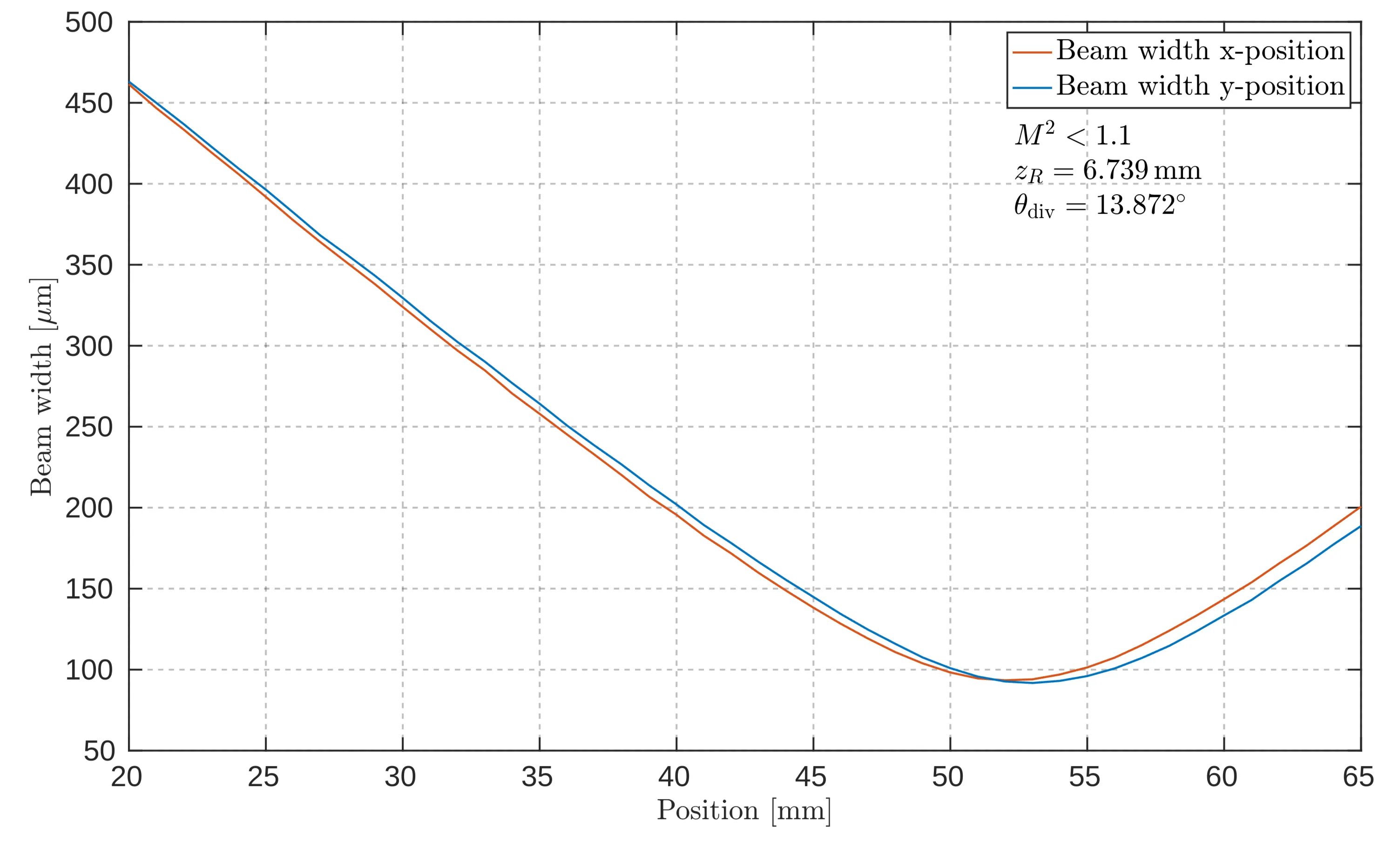
Results of the $M^2$ measurement using a beam slit profiler. The stage moved a total of $45\text{ mm}$ to determine that $M^2<1.1$, with a Rayleigh length of $z_R=6.739\text{ mm}$ at the focus. The divergence angle was calculated to be ${\theta }_{\text{div}}={13.872}^{\circ }$.

3.2.2 Spectrum Analyser

A small portion of the output power, approximately $50\mu \text{W}$, is directed to an optical spectrum analyser (OSA) to measure the laser output spectrum. The OSA reveals that when the laser is mode-locked, the central wavelength is at $1029.75\text{ nm}$ with a full-width at half-maximum (FWHM) of $1\text{ nm}$, consistent with the emission wavelength of Ytterbium. The laser operates in continuous wave mode at lower pump powers, displaying a narrow line-like spectrum.

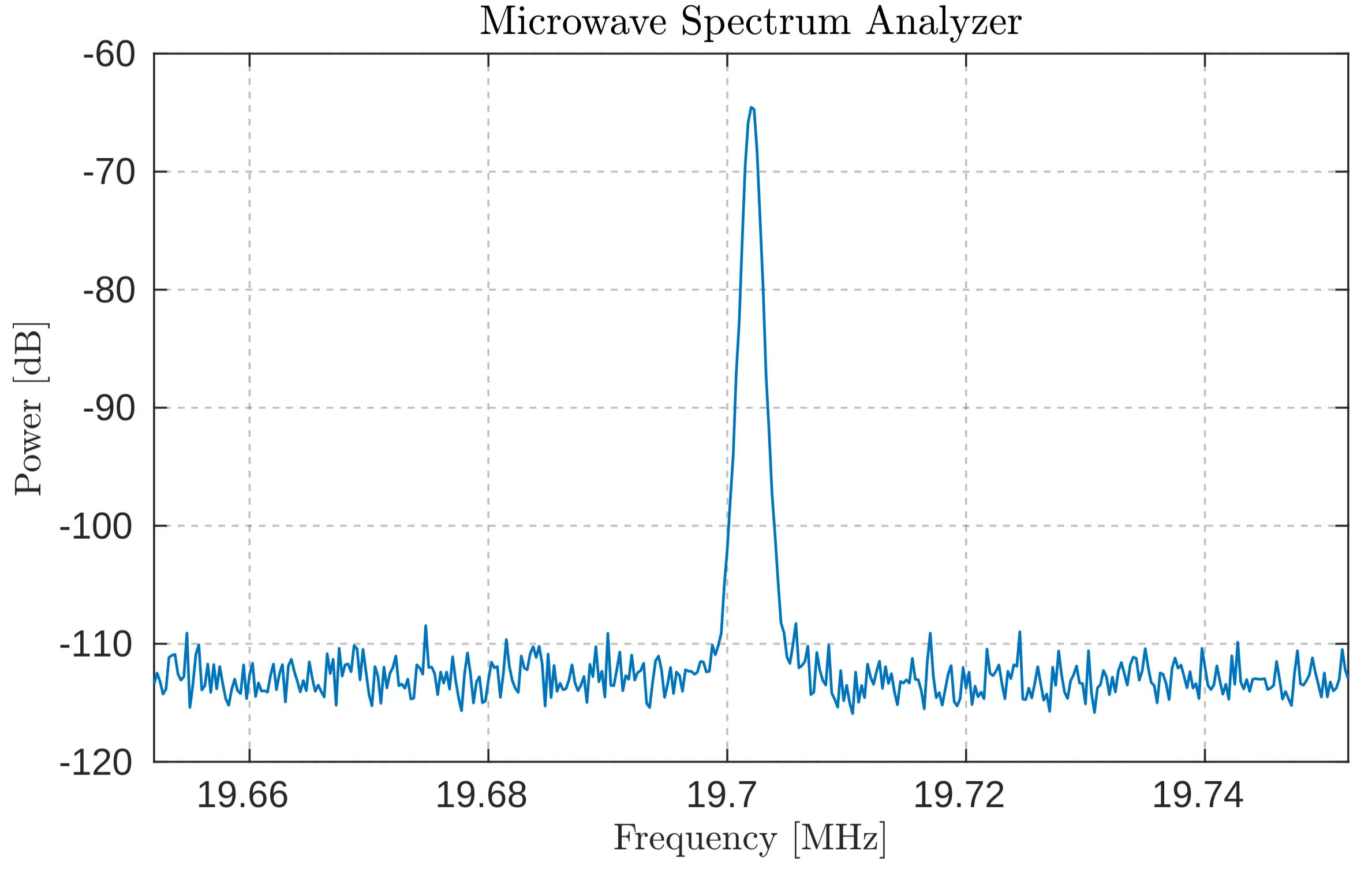
Another small fraction of the laser power is directed to a microwave spectrum analyser (MSA) to obtain the frequency spectrum, which includes multiple harmonics of the mode-locked signal. A photodiode converts the optical signal into an electrical one for analysis by the MSA. s expected, as shown in the next-next figure, multiple peaks corresponding to harmonics of the repetition rate, $f_{\text{rep}}=19.7\text{ MHz}$, are observed. The next figure displays a single peak captured by the MSA, corresponding to the laser's repetition frequency of $19.7\text{ MHz}$. The measurement was performed with a resolution bandwidth of $300\text{ Hz}$.

Further diagnostic measurements at different pump powers are detailed in the appendix.

3.2.3 Autocorrelation

We use an intensity autocorrelator to determine the pulse width and the temporal structure of the laser output. The methodology and principles behind this technique are discussed in detail in the appendix. The measured pulse width is approximately $1037\text{ fs}$, close to the transform-limited pulse duration of $1000\text{ fs}$, as determined from the OSA measurement. The following figure shows the diagnostic results from the spectrum analysers and the autocorrelator. The dashed fit represents an ideal soliton pulse.

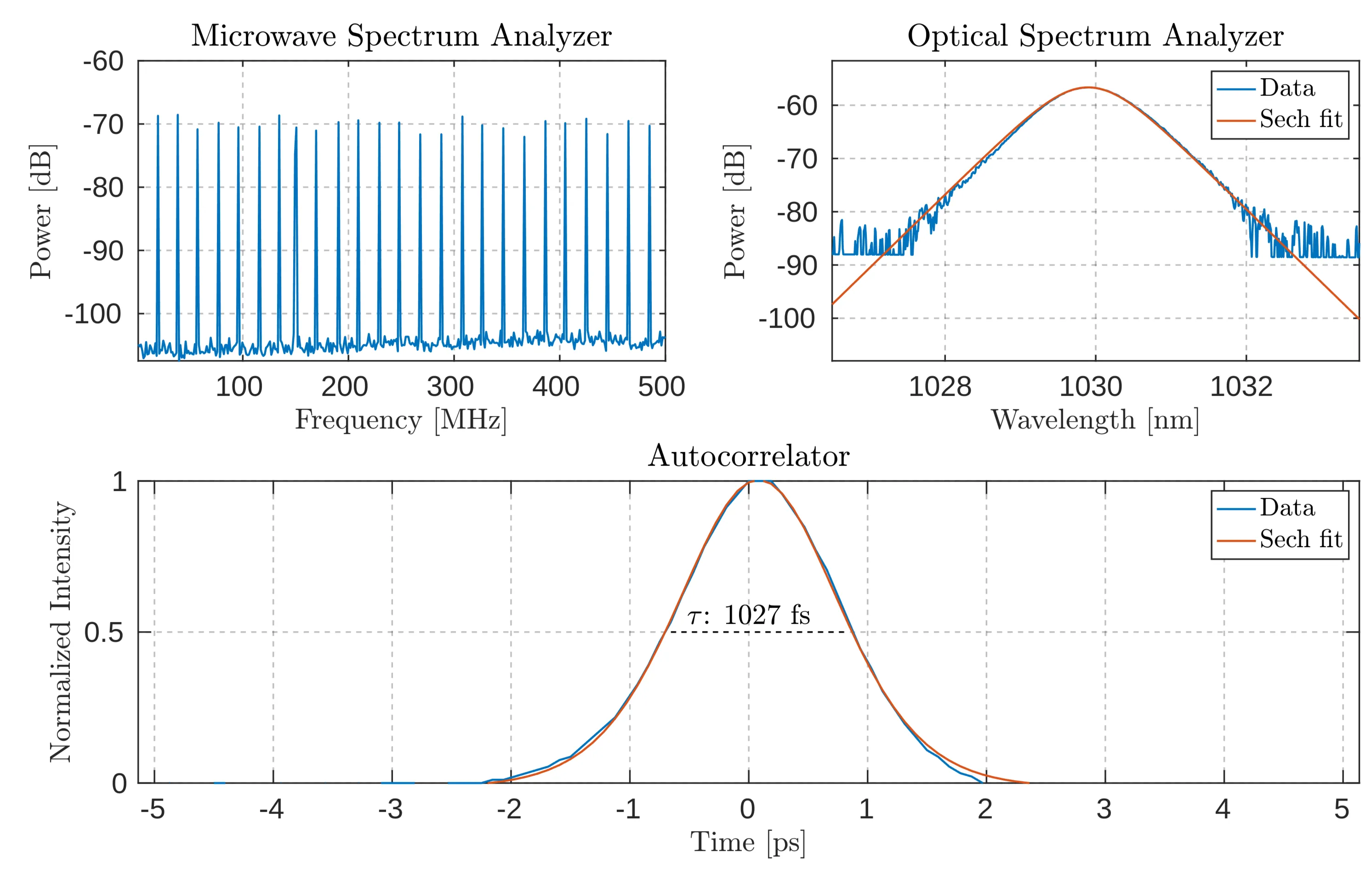
Combined diagnostic results from the microwave spectrum analyser (MSA) measured with $1\text{ kHz}$ resolution bandwidth, autocorrelator, and optical spectrum analyser (OSA). The MSA reveals multiple harmonics corresponding to the laser's repetition rate, confirming stable mode-locking. The autocorrelator provides the pulse width measurement, while the OSA shows the laser's output spectrum, highlighting a central wavelength of $1029.75\text{ nm}$ with a $1\text{ nm}$ FWHM, consistent with the emission wavelength of Ytterbium. The red line represents an ideal soliton pulse fit.

3.3 Fibre Coupling

In this section, the path from the laser cavity to the hollow-core fibre is traced and explained in detail.

3.3.1 Mode-Field Diameter

The specified mode-field diameter (MFD) of the fibre is $42\mu \text{m}$. To efficiently couple into the fibre, the beam needs to be collimated to a much smaller size compared to its size at the output coupler (OC). Simulations estimate the beam waist size at the output coupler to be $335\mu \text{m}$ in both the horizontal and vertical axes (beam waist sizes are given with respect to their $1/e^2$ radius unless otherwise specified). Thus, a magnification factor of $M=16$ is needed. A straightforward method to reduce the waist size is to build a telescope consisting of two lenses with focal lengths $f_1$ and $f_2$. The first lens is placed at a distance $f_1$ from the OC, and the second lens is positioned $f_1+f_2$ from the first lens. Both lenses should satisfy $M=\frac{f_1}{f_2}=16$ to reduce the waist size to a radius of $21\mu \text{m}$. A reasonable combination of lenses is $f_1=2000\text{ mm}$ and $f_2=125\text{ mm}$, which should achieve this size. To verify that the desired waist size is reached, the single-plane beam profiler Beam'R2 from DataRay is used, capable of profiling beams as small as $2\mu \text{m}$. However, results showed that the beam was larger than expected at the focus and slightly elliptical, with a 4:3 ratio between the horizontal and vertical axes. This is likely due to the non-zero angle of incidence in the horizontal direction inside the oscillator, which caused the beam to become asymmetrical. This effect persisted even after replacing the SESAM, indicating that the SESAM was not the primary cause. To correct this issue, an additional telescope that works in only one axis, using cylindrical lenses, is required.

Two lenses should have focal lengths with an absolute ratio of 4:3. However, to avoid creating a focus between these two lenses (which could introduce additional artefacts due to high intensity), a combination of convex and concave lenses is used. This is realised using $f_{1,\text{cyl.}}=100\text{ mm}$ and $f_{2,\text{cyl.}}=-75\text{ mm}$, spaced at $100\text{ mm}$ and $125\text{ mm}$ behind the OC, respectively. The next figure shows the beam waist size of the horizontal and vertical axes, where position 0 is the OC of the laser cavity. The beam is assumed to be elliptical at the OC with a 4:3 ratio between both axes.

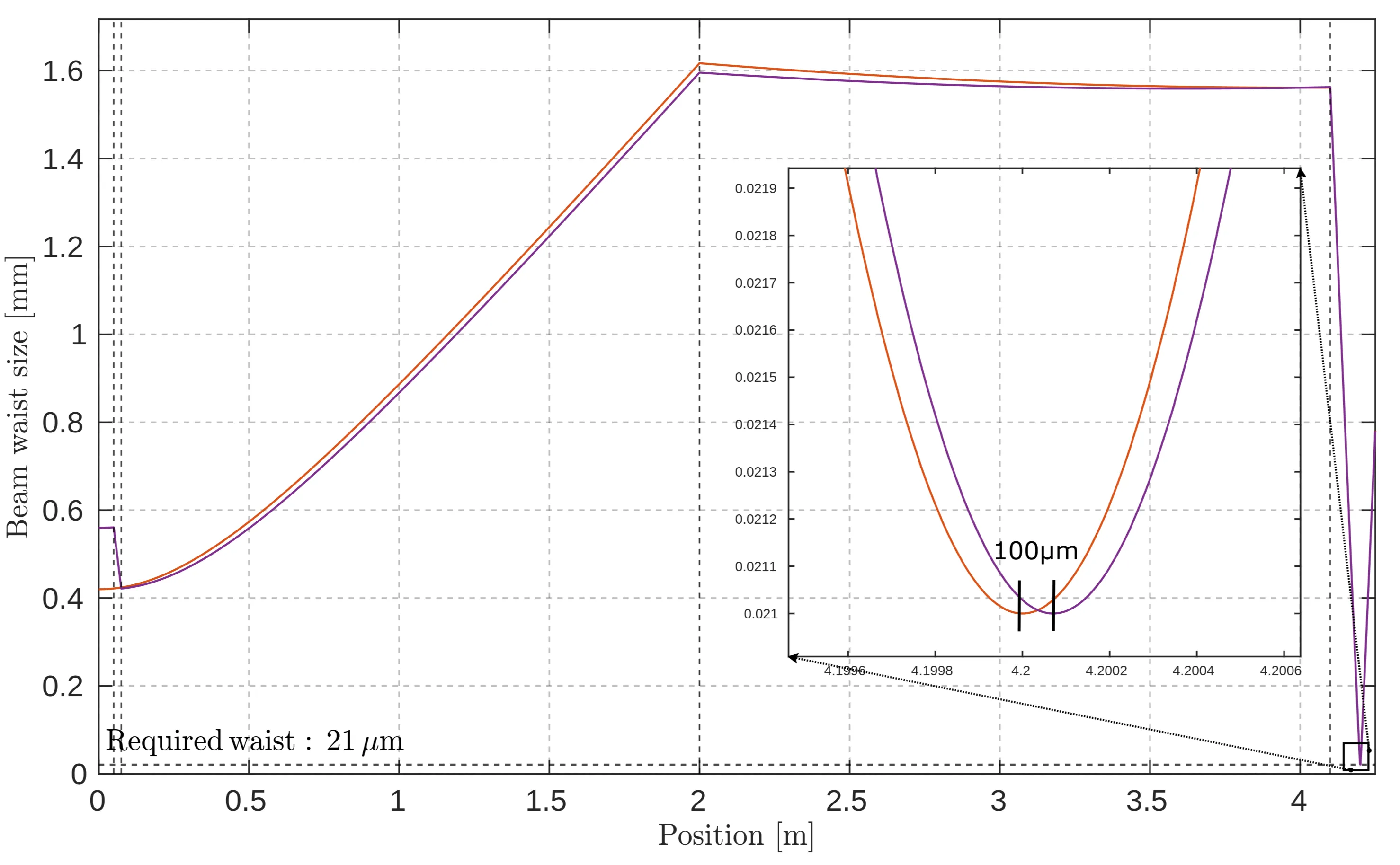
Beam waist evolution as the laser passes from the output coupler of the cavity through the telescope, which optimises the beam for fibre coupling. The orange and violet curves represent the beam waist sizes in the horizontal and vertical axes, respectively. The zoomed-in section highlights slight astigmatism between the horizontal and vertical foci at the fibre's focal point.

The simulation suggests that this setup introduces slight astigmatism, with a spacing of roughly $100\mu \text{m}$ between the foci of the two axes. While strong astigmatism could significantly reduce coupling efficiency and increase the risk of damaging the fibre, this small amount of astigmatism does not appear to cause significant issues. This is evidenced by the fact that the experiments still achieved a good coupling efficiency of up to $85\mathrm{\%}$. If astigmatism had been a significant issue, the coupling efficiency would be much lower.

3.3.2 Power Tuning

Another important consideration is power tuning. Even if everything works as expected, it is dangerous to immediately send full power into the fibre, especially if beam stabilisation has not yet been achieved. A common issue with SESAMs is Q-switching: initially, the output power can be finely tuned from $0\text{ W}$ to about $4\text{ W}$ before Q-switching occurs. Typically, the pump power is ramped up quickly to minimise time spent in the Q-switching regime, reducing the risk of damaging components or the thin-disk itself. However, this means the power cannot be slowly and continuously tuned for values above $4\text{ W}$. A simple yet elegant solution to this problem is to use a combination of a half-wave plate (HWP) and a thin-film polariser (TFP). By rotating the polarisation, the fraction of the beam that is reflected or transmitted by the TFP can be controlled. A second pair of HWP and TFP allows for even finer control. This way, the HWP can be adjusted to minimise power reaching the fibre at low laser output power. The laser can then be safely mode-locked, and the HWP can be rotated to increase the power directed into the fibre.

3.3.3 Polarisation

While the fibre has no defined birefringence, induced birefringence effects along preferential polarisation angles might occur due to the non-radially symmetric structure of the photonic crystal in the fibre and fibre bending. Indeed, the input polarisation can change the beam shape and far-field profile. Incorrect polarisation also dramatically increases the fibre's sensitivity to touch. Therefore, a half-wave plate is placed before the fibre to control the input polarisation.

3.3.4 Fibre Coupling

As mentioned earlier, the specified MFD of the fibre is $42\mu \text{m}$. This is a relatively large MFD compared to other optical fibres, meaning the beam position is less critical for efficient coupling into the fibre. However, the angular alignment becomes much more sensitive. Two coupling mirrors allow fine-tuning of the angular alignment, while a standard three-axis linear translation stage allows the fibre entry position adjustment. This setup keeps the coupling process relatively straightforward, unlike using a five-axis stage for the fibre, especially when the two coupling mirrors are already present.

3.3.5 Pressure and Gas System

The simulations assume a pressure of $25\text{ bar}$ with Xenon in the fibre. However, at this pressure, Xenon costs approximately $4,000\text{ CHF per litre}$, making it impractical for initial tests. A more cost-effective gas, Argon, was used at a pressure of $10\text{ bar}$ to ensure the gas control system functions properly. During testing, the system initially exhibited a minor leak, resulting in a pressure drop of $2\text{ bar}$ over $8\text{ hours}$. Attempts to repair the leak led to further complications, making the system unable to hold pressures over $5\text{ bar}$, requiring the entire system to be returned for a complete reconnection of the fibre.

3.4 Grating Spectrometer

As discussed in Section 2.6, applying high pressure to a gas with a high nonlinear refractive index and allowing the pulse to propagate will generally lead to significant spectral broadening. For example, a pulse that initially had a full-width at half-maximum (FWHM) of $1\text{ nm}$ may broaden to an FWHM of approximately $50\text{ nm}$. Since the focus is on the spectral regions where the gain is high and the power is sufficient for measurement, it is essential to filter a specific part of the spectrum selectively. This can be accomplished using a grating spectrometer, which allows for precisely selecting the wavelength range of interest. The principle behind this setup is straightforward: the fibre output is directed onto a blazed grating, which disperses the light, causing different wavelengths to have distinct wavevectors. By using a narrow slit, we can effectively select the desired spectral region. The next figure shows the schematic working principle of this spectrometer:

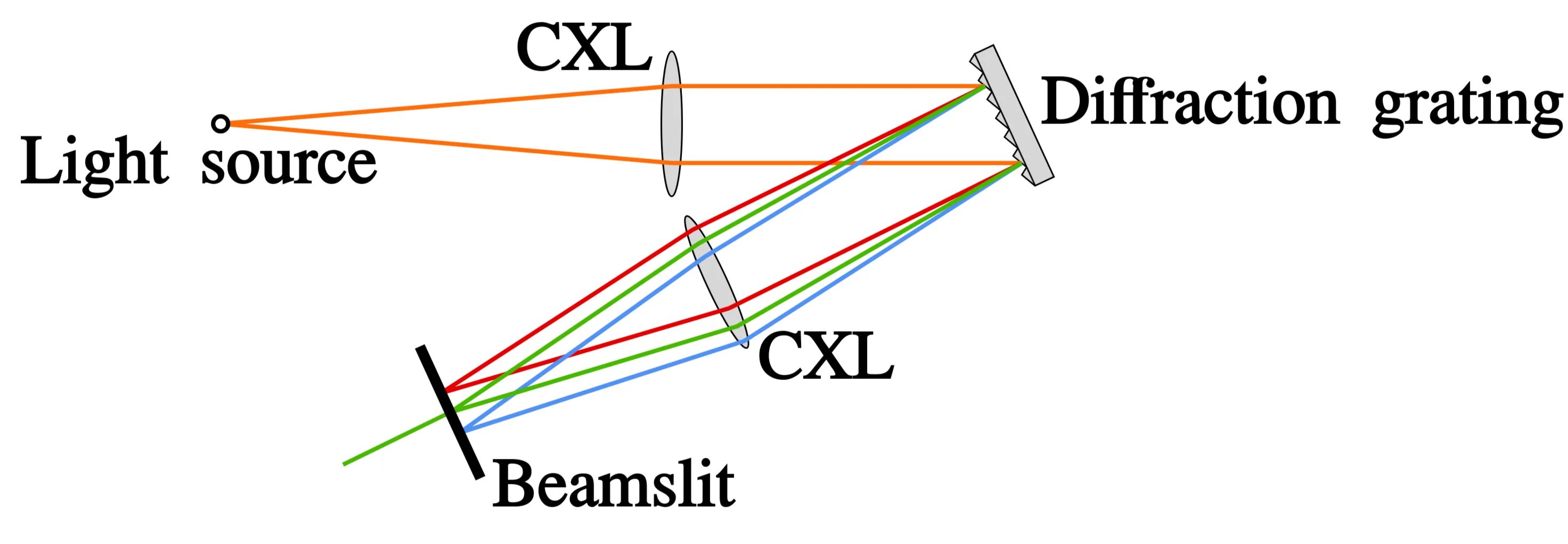
Schematic diagram of a grating spectrometer. The convex lens (CXL) focuses the incoming light and resolves the spectral overlap, allowing each wavelength to be detected at distinct positions on the detector.

A grating functions by altering the incident phase and amplitude of incoming light to separate different wavelengths. The interference pattern created depends on the grating's geometry. In this thesis, a blazed grating is used, characterised by its blaze wavelength, groove spacing $d$, and blaze angle $\gamma$. The angles are measured relative to the surface normal, and the groove spacing can be expressed in terms of groove density $d=1/N$, where $N$ is typically given in lines per millimetre. The blaze angle $\gamma$ is the angle between the facet normal and the surface normal, and adjusting this angle allows for tuning the grating's efficiency.

The grating equation relates the angle of incidence ${\alpha }_i$ with the diffraction angle ${\beta }_m$, depending on the diffraction order $m$ and the wavelength $\lambda$:

No diffraction pattern is observed in the zeroth order mode ($m=0$), making this case uninteresting. In this mode, the only solution is ${\alpha }_i=-{\beta }_m$, meaning the angle of incidence equals the angle of diffraction, analogous to specular reflection on a flat surface. This result is independent of wavelength and thus provides no spectral information.

At twice the blaze angle, we find:

A special case is the so-called Littrow configuration, where the grating efficiency is maximised. This occurs when ${\alpha }_i={\beta }_m$ and $m>0$. Referring to the grating equation discussed above, we find:

where ${\theta }_L$ is the Littrow angle, and ${\lambda }_D$ is the design wavelength, defined as the wavelength at which the grating is most efficient. The Littrow angle depends on the most intense order ($m=1$), and at $\lambda ={\lambda }_D$, we have ${\theta }_L=\gamma =\arcsin \left(N\frac{m{\lambda }_D}{2}\right)$. Since arcsin returns real values only for inputs between -1 and 1, this also defines a maximum groove density $N_{\text{max}}\le \frac{2}{m{\lambda }_D}$.

The angular dispersion $D$ is given by:

Next, we analyse the free spectral range. Reflected light of different orders may overlap, but this can be avoided for the wavelength range $[{\lambda }_1,{\lambda }_2]$ if:

holds for ${\lambda }_1<{\lambda }_2$. Fortunately, this is not an issue with $m=1$, as can be easily verified by considering the central wavelength of $1030\text{ nm}$.

Another crucial factor is the spectral resolution, which limits the minimum wavelength differences that can be resolved by using a diffraction grating. There are two approaches to determine whether two wavelengths can be resolved:

1. Resolving Power: The resolving power is defined as $R=\frac{\lambda }{\mathrm{\Delta }\lambda }=m{N}_{\text{ill}}$, where $\mathrm{\Delta }\lambda$ is the smallest resolvable difference from $\lambda$, and $N_{\text{ill}}$ is the number of illuminated grooves. This allows us to estimate:

   $$\mathrm{\Delta }\lambda =\frac{\lambda }{m{N}_{\text{ill}}}=\frac{\lambda \cos ({\theta }_i)}{m2Nw},$$

   where $w$ is the beam waist on the grating, ${\theta }_i$ is the angle of incidence, and the factor of 2 accounts for the beam waist being a radius. With the beam size of this TDL, this results in a spectral resolution below $0.5\text{ nm}$ for a grating with $600\text{ l/mm}$ and a Littrow angle of ${18}^{\circ }$. The next figure shows the beam waist after the fibre, demonstrating that the chosen setup with lenses results in a collimated beam on the grating, justifying the approximation of ignoring the Gaussian nature of the beam.
   
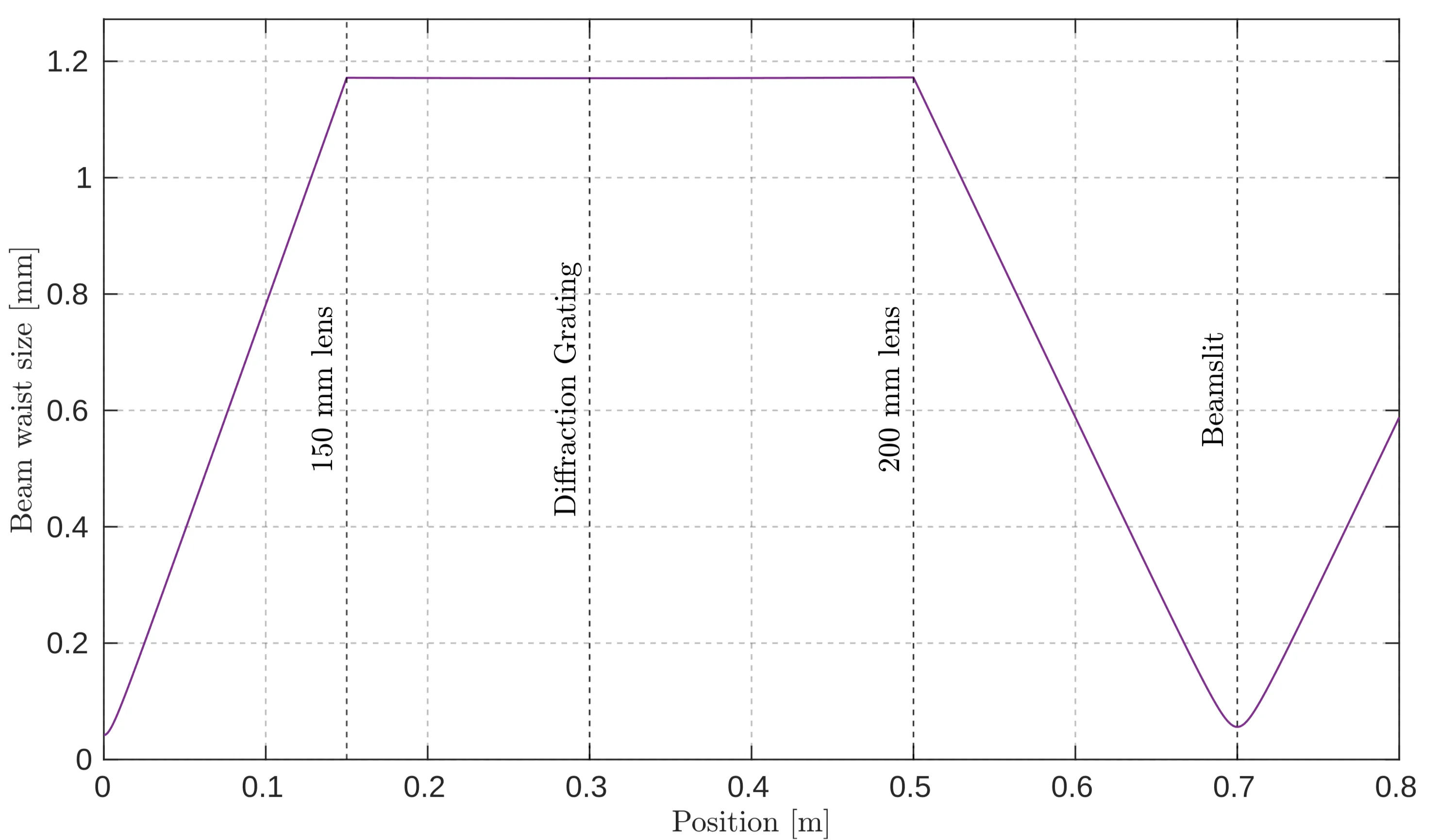
   Evolution of the beam waist after exiting the fibre and passing through a $150\text{ mm}$ focusing lens, which collimates the beam to a large radius at the grating. The beam slit is positioned at the focal point after reflection from the grating to select a specific wavelength range.

2. Gaussian Optics: First, assume the grating behaves like an ordinary mirror, not affecting the beam waist. Then, ray transfer matrix analysis simulation shows that the focus behind the second lens will have a waist $w_{\text{exit}}=50.4\mu \text{m}$. Now, consider the problem: If this behaviour holds for every spectral component, what must be the wavelength difference $\mathrm{\Delta }\lambda$ for their positions in the focus after the lens to differ by $w_{\text{exit}}$? The spectrum will not be smeared if their separation is larger than their individual waist sizes. This problem simplifies near the Littrow configuration, as the projection of two spots from two spectral components onto a common surface is equal, even for different spectral components. The spatial distance between two wavelengths is:

   $$\mathrm{\Delta }x=f_2(\sin ({\beta }_m({\lambda }_2))-\sin ({\beta }_m({\lambda }_1)))\approx f_{2}mN\mathrm{\Delta }\lambda$$

   where ${\beta }_m(\lambda )=\arcsin (m\lambda N-\sin {\alpha }_i)$ is the diffraction angle for a given wavelength $\lambda$ and incident angle ${\alpha }_i$, and $f_2$ is the focal length of the lens after the grating. Setting $\mathrm{\Delta }x=2w_{\text{exit}}$, we obtain:

   $$\mathrm{\Delta }\lambda =2\frac{w_{\text{exit}}}{f_{2}mN}$$

   which is approximately $0.3\text{ nm}$. Since this value is lower than the resolution obtained using the resolving power, smearing due to the Gaussian nature of the beam is unlikely to be problematic, as the resolving power would not have permitted higher resolution in the first place.

In summary, this setup allows resolving spectral features as small as $0.5\text{ nm}$.

3.5 Characterisation

To fully characterise the laser noise, several key factors must be considered. Firstly, the photodiode (PD) must operate within its linear range, where its voltage response remains proportional to the incident power and does not become saturated. A low-pass filter might be necessary to suppress peaks at the repetition frequency, preventing potential damage to the oscilloscope or signal spectrum analyser.

Suppose amplifiers are employed to enhance the signal. In that case, verifying that they provide consistent gain across the relevant frequency range is essential, meaning they should have a flat frequency response. Additionally, the repetition rate must not exceed the amplifiers' saturation limits. Since consistent gain is typically achievable only within specific frequency bands, multiple amplifiers might be required for different measurements, and their results may need to be combined at a common reference point.

3.5.1 Photodiode Characterisation

Two photodiodes were evaluated for measuring the laser noise: Thorlabs' large-area ($75.4{\text{ mm}}^2$) silicon photodetector DET100A/M and the FDS100 silicon photodiode. The DET100A/M operates over wavelengths from $350\text{ to }1100\text{ nm}$, with a rise time of $43\text{ ns}$, while the FDS100, with a smaller active area of $3.6\text{ mm}\times 3.6\text{ mm}$, offers a faster rise time of $10\text{ ns}$. Increasing the applied reverse bias enhances the photodiode's responsivity due to improved charge collection efficiency. Silicon photodiodes are favoured for their low cost, low dark current, and high-speed performance. The DET100A/M is operated at a fixed reverse bias of $10\text{ V}$, while the FDS100 may operate with a reverse bias of up to $25\text{ V}$. The following measurements were done at $24\text{ V}$ reverse bias.

To assess the performance of the photodiodes, the average generated voltage response was measured against the incident power. The generated voltage was $50\mathrm{\Omega }$ terminated and measured using either a multimeter or an oscilloscope. The multimeter provides the average voltage, while the oscilloscope allows for peak voltage measurements. However, peak voltage measurements can be misleading due to noise and short-term disturbances, often resulting in artificially high readings. The next two figures present the measured average voltages, with a reverse bias of $24\text{ V}$ applied to the FDS100 photodiode.

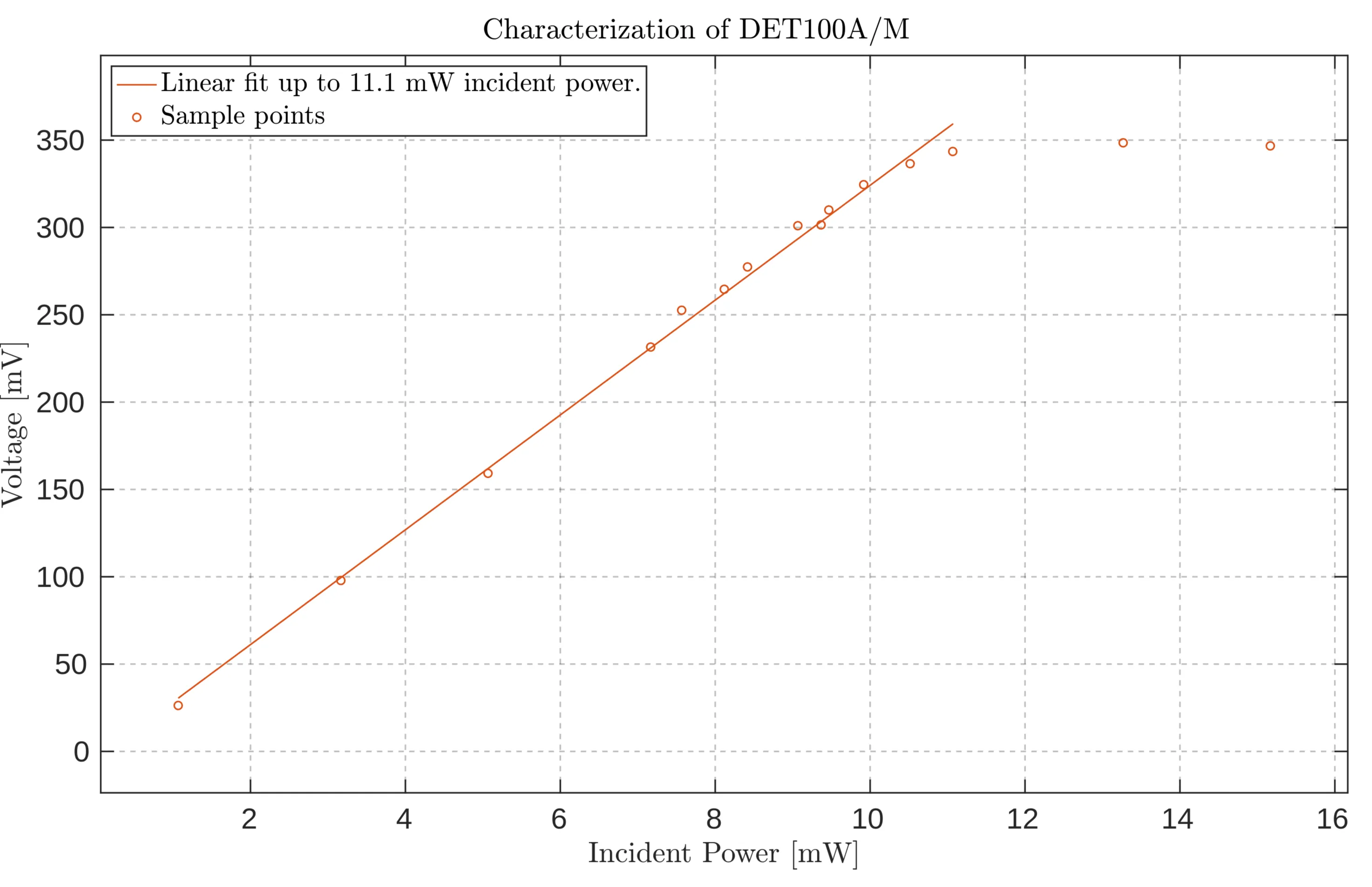
Characterisation of the silicon photodiode DET100A/M, showing a linear response for chosen points up to $11.1\text{ mW}$ of incident power. Points where the photodiode is already saturated are excluded from the linear fit.

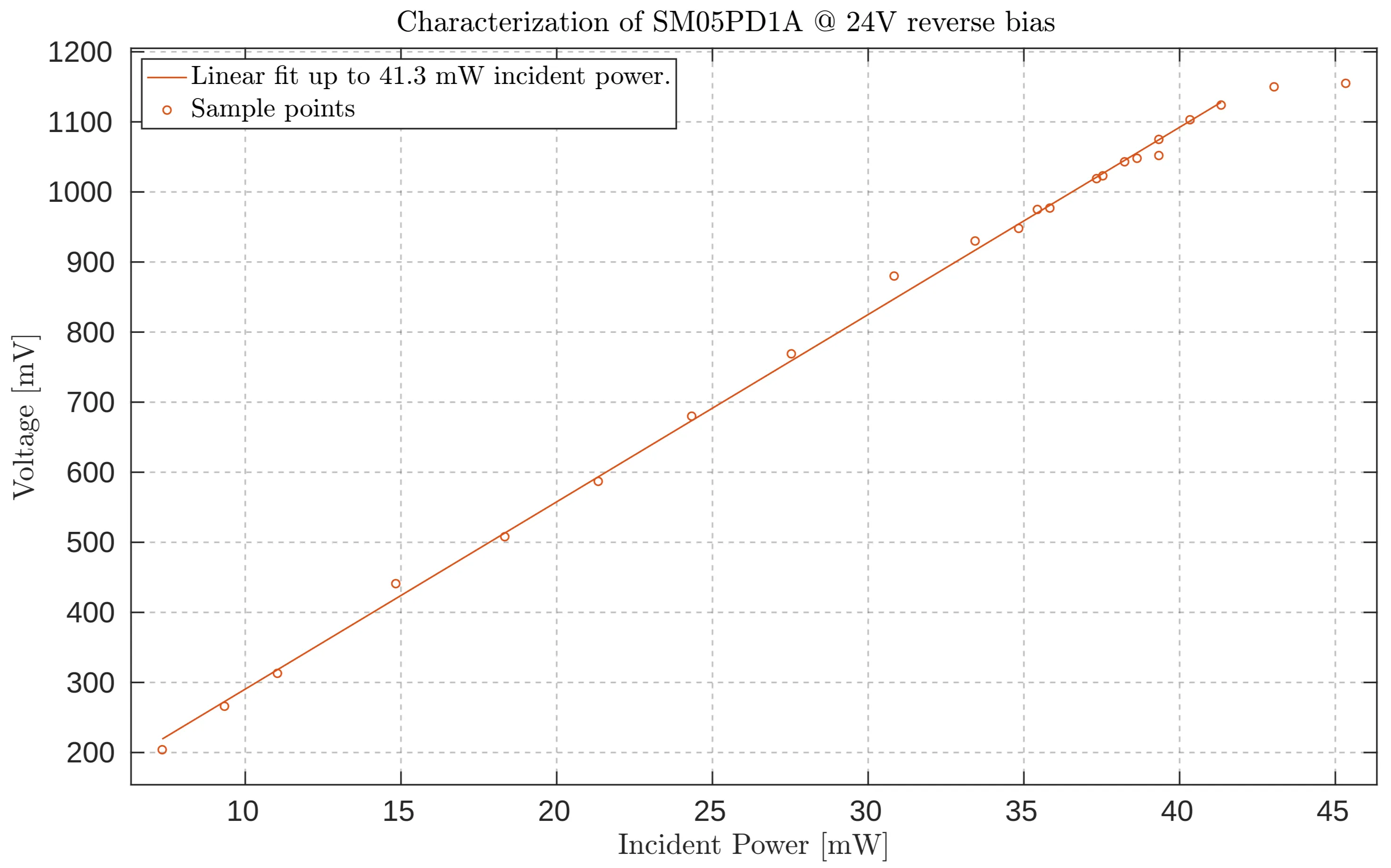
Characterisation of the silicon photodiode FDS100, showing a linear response for chosen points up to $41.3\text{ mW}$ of incident power. Points where the photodiode is already saturated are excluded from the linear fit.

These results suggest that the small-area FDS100 photodiode should enable the measurement of lower shot-noise levels. The shot-noise limit, expressed in units of $\text{dBc/Hz}$, is given by:

where $q$ is the electron charge, $R=50\mathrm{\Omega }$ is the termination resistance, and $V_{\text{DC}}$ is the generated average (DC) voltage. A detailed derivation is provided in the relevant theoretical section. Comparing the generated DC voltages at the maximum point of the linear range ($1100\text{ mV}$ for DET100A/M and $320\text{ mV}$ for FDS100):

Therefore, in theory, the FDS100 photodiode should allow for the measurement of lower shot-noise levels. However, the results obtained did not align with expectations, as shown in the next two figures:

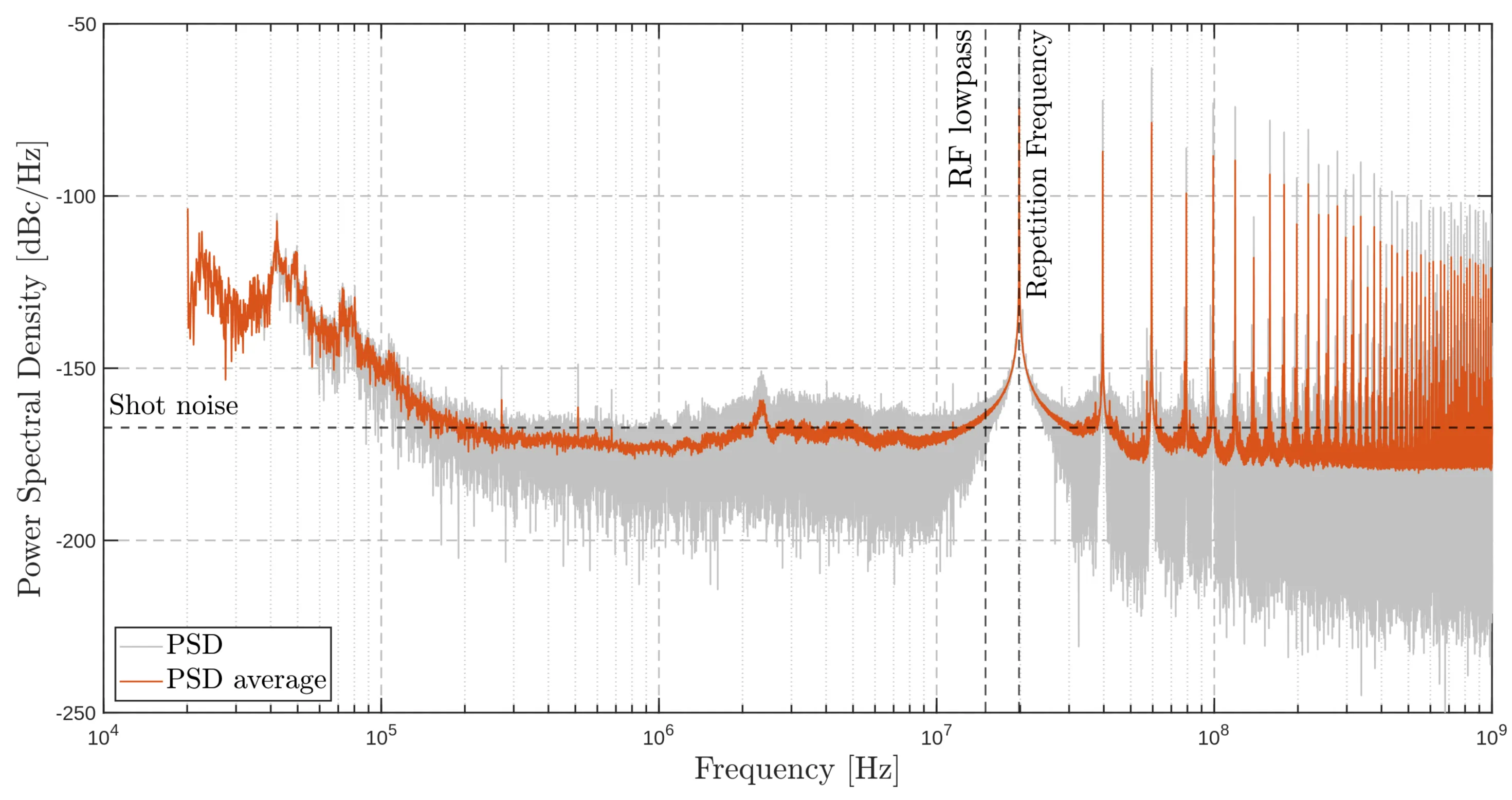
Noise PSD measured with the FDS100 photodiode at $24\text{ V}$ reverse bias and $32\text{ mW}$ incident power. The noise trace falls below the expected shot-noise limit, which is unexpected as the photodiode should not saturate at this incident power level.

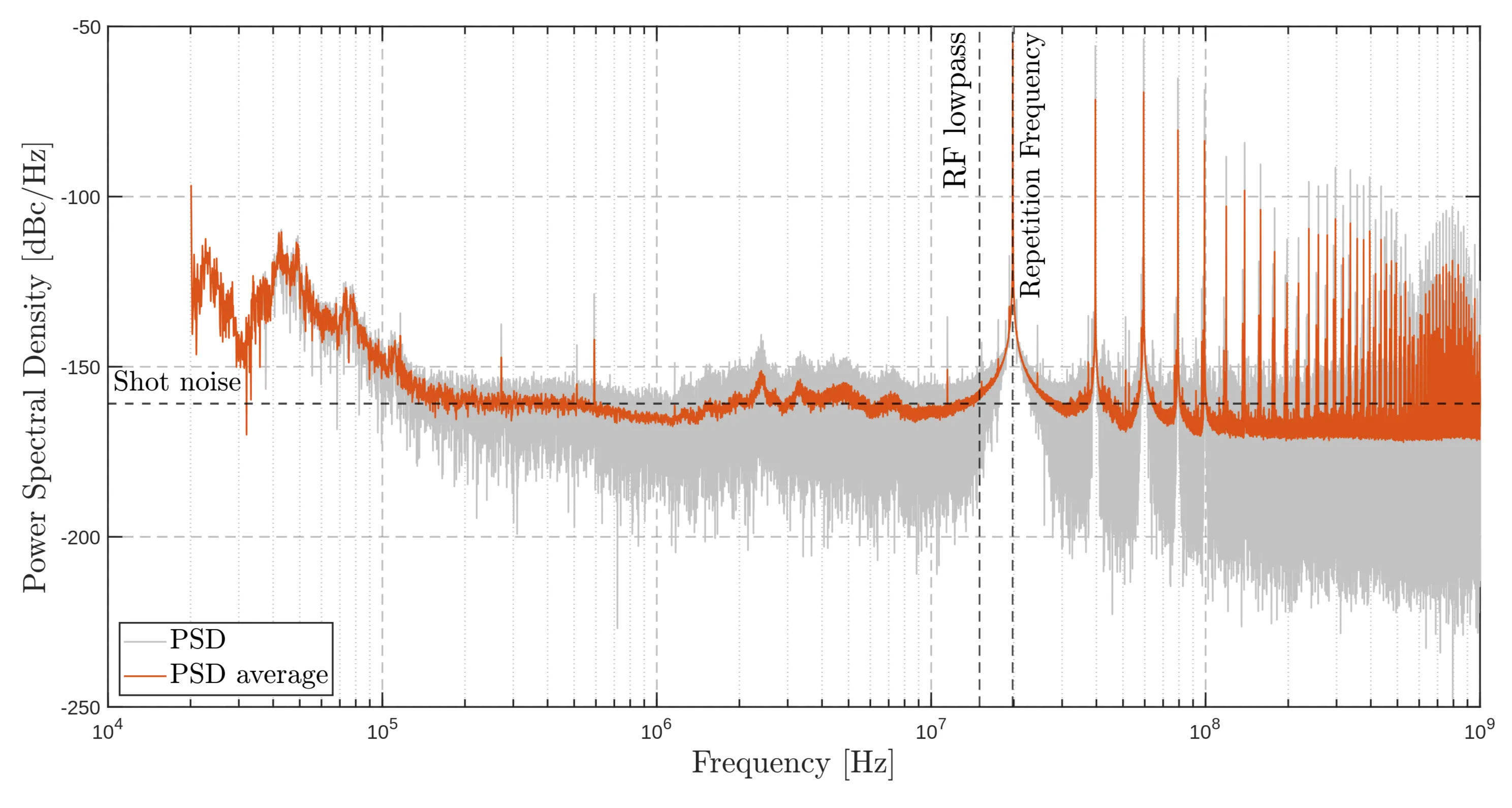
Noise PSD measured with the FDS100 photodiode at $24\text{ V}$ reverse bias and $8\text{ mW}$ incident power. Surprisingly, despite the lower incident power, the noise trace again drops below the shot-noise limit around $1\text{ MHz}$. Given the lower power, saturation should not occur, making this result equally unexpected.

As a result, the final noise measurements were carried out using the DET100A/M photodiode. The choice of photodiode plays a crucial role in determining the optimal measurement settings. With the appropriate photodiode selected, it is essential to ensure the measurements are taken within the photodiode's linear range, avoiding saturation. Saturating the photodiode can result in an artificially reduced shot-noise level, compromising the accuracy of the measurement results.

3.5.2 Noise Characterisation

Before delving into noise characterisation, it is essential to differentiate between the various types of laser noise when measuring with an oscilloscope: shot noise, amplifier noise, and oscilloscope (or quantisation) noise. Amplifier noise includes contributions from thermal (Johnson) noise and the amplifier's noise figure, increasing with the amplifier's gain and temperature. The noise power of the amplifier can be estimated as:

where $g$ is the amplifier's voltage gain, $I_{\text{Johnson}}$ is the Johnson noise current, NF is the amplifier's noise figure, and $l_{\text{output}}$ is the output loss factor. On the other hand, oscilloscope noise arises primarily from the quantisation process and the oscilloscope's inherent noise floor. This includes limitations due to the number of bits used and the voltage resolution. Oscilloscope noise can be reduced or minimised by choosing a high voltage resolution (for instance, a small voltage per division), such as zooming in on the oscilloscope as much as possible. With the correct settings on the oscilloscope, the analysis reveals that shot noise is the dominant noise source, allowing us to neglect oscilloscope and amplifier noise in the following discussions safely.

The next step involved performing the noise measurements using the selected photodiodes. The RIN spectrum of solid-state lasers typically exhibits much higher noise levels at low frequencies compared to the shot-noise limit at higher frequencies, so it is difficult to analyse the entire spectrum with a single, sensitive measurement. To overcome this, the RIN was measured separately in both the low- and high-frequency regions, each using different amplifiers optimised for their respective frequency ranges. For the low-frequency part, a $5\text{ MHz}$ low-pass filter was used to measure the noise with a signal source analyser (SSA), while the high-frequency region was analysed using an oscilloscope. The reason for using two different measurement devices is that the SSA exhibited unusual behaviour in the noise range of around $1\text{ MHz}$ when applying a $5\text{ MHz}$ low-pass filter. This occurred because such filters affect frequencies below their specified cut-off, thus interfering with the noise measurements. However, a $10\text{ or }15\text{ MHz}$ filter could not be used with the SSA due to saturation issues.

On the other hand, the oscilloscope allowed the use of a $15\text{ MHz}$ low-pass filter, effectively preventing overload. After completing both measurements, the power spectral densities were combined during post-processing. This approach is similar to the noise measurement method employed by other researchers.

Low-Frequency Region
For the frequency range from $1\text{ Hz to }100\text{ kHz}$, we employed the DLPCA-200 transimpedance amplifier, set to a gain of $30\text{ dB}$. This amplifier operates with a flat amplification profile from $1\text{ Hz (DC) to }500\text{ kHz}$. The DLPCA-200 is characterised by low noise, with an input noise voltage of $4\text{ nV}/\sqrt{\text{Hz}}$.

To convert the signal from voltage to $\text{dBc/Hz}$, we require the carrier spectral density $S_c(f)$ and the signal spectral density $S_V(f)$. The carrier density is obtained by terminating the amplifier output with a $50\mathrm{\Omega }$ resistor and measuring the resulting DC voltage $V_{\text{DC}}$ using a multimeter. The amplifier is then switched to AC coupling, so the SSA does not overload. The carrier spectral density is calculated as follows:

where the factor of $1/2$ accounts for the effective resistance. The signal power spectral density $S_V(f)$ is derived from the time-discrete signal, which is sampled at a rate $f_s$ with $N$ data points:

which, like the carrier PSD, is expressed in units of volts squared. The spectral noise density is then calculated as:

High-Frequency Region
For frequencies above $60\text{ kHz}$, the DUPVA 1-70 voltage amplifier was utilised, which provides a flat amplification profile up to multiple GHz. The flat amplification profile starting from $60\text{ kHz}$ has been experimentally confirmed in past experiments. In this higher frequency region, the measurement procedure is adjusted slightly, as only the AC part of the signal is amplified. The DC component is split off with a Bias-T, then terminated with a $50\mathrm{\Omega }$ resistor, and measured with a multimeter for normalisation.

When calculating the carrier spectral density in this region, the actual gain of the voltage amplifier must be considered. Although the DUPVA 1-70 was expected to deliver a $40\text{ dB}$ gain (corresponding to a voltage gain $g=100$), subsequent measurements revealed an actual gain of $g\approx 86.23$, corresponding to an amplification of $38.17\text{ dB}$. Accounting for this, the carrier spectral density is given by:

To obtain a meaningful shot-noise level, the DC voltage measured with this voltage amplifier is used. The shot-noise level can be determined using:

where $R=50\mathrm{\Omega }$ is the termination resistance and $q$ is the electron charge. For the laser presented in this work, the shot-noise limited detection is $S_{\text{shot}}=-162\text{ dBc/Hz}$.

3.5.3 Optimising Sampling Rate for Accurate Noise Measurement

To conduct a meaningful noise measurement, a crucial factor to consider is the sampling rate of the measuring device - in this case, Teledyne Lecroy's WavePro 254 HD oscilloscope, which supports up to $20\text{ GS/s}$. According to the Nyquist-Shannon sampling theorem, the sampling rate must be greater than twice the signal bandwidth to ensure accurate signal reconstruction and avoid aliasing. Given that we expect the laser's noise to approach the shot-noise limit around the MHz frequencies - frequencies beyond which are less relevant for our purposes - one might initially assume that a sampling rate of a few megasamples per second would suffice to capture all relevant noise components. However, this assumption can be misleading.

To clarify this, it is useful to state the theorem more precisely in Shannon's original form:
The Nyquist-Shannon Sampling Theorem states: If a signal $x(t)$ contains no frequencies higher than $B$ Hertz, then it can be completely reconstructed by a sequence of points spaced less than $\frac{1}{2B}$ seconds apart.

Thus, assuming that there is no significant information above a few megahertz could be problematic. Aliasing can cause noise from higher frequencies to be sampled in a way that it appears at lower frequencies, potentially interfering with the measurements at frequencies of interest. This is why merely selecting a low sampling rate may not be sufficient; careful consideration of the highest frequencies present in the signal is essential to avoid misinterpreting the noise characteristics.

The careful reader might also wonder why the highest available sampling rate was not used. There are practical constraints, such as the maximum data file size and the speed at which the data can be processed. The oscilloscope allows for saving up to $5\times {10}^9$ data points per run, which inherently limits the duration of the measurement and, consequently, the minimum frequency that can be probed. Therefore, the goal is to choose the lowest sampling rate that avoids aliasing while maximising the measurement duration.

A series of experiments were conducted to determine the optimal sampling rate for measuring the noise spectral density of the laser. Noise measurements were compared under two conditions: a) with the laser light input and b) with the laser light blocked. The next five images display these comparisons, each consisting of three subplots: the top subplot shows the noise spectral density with the laser light input, with the raw Fourier transform in grey and the averaged trace in orange. The middle subplot shows the noise measurement with the beam blocked, again in raw (grey) and averaged (orange) traces. The bottom subplot presents the difference between the raw traces (grey) and the averaged traces (orange), with a black horizontal line indicating the zero mark.

Sample rate: $50\text{ MS/s}$:

Noise measurement comparisons at a sampling rate of $50\text{ MS/s}$: Top subplot shows the laser light input; middle subplot shows the blocked beam; bottom subplot displays the difference between raw and averaged traces. At this rate, the oscilloscope fails to capture meaningful data above $1\text{ MHz}$ because the difference is too low with $1\text{ dB}$, indicating inadequate sampling.

Sample rate: $100\text{ MS/s}$:

Noise measurement comparisons at a sampling rate of $100\text{ MS/s}$: Top subplot shows the laser light input; middle subplot shows the blocked beam; bottom subplot displays the difference between raw and averaged traces. The higher sampling rate captures more accurate data than $50\text{ MS/s}$ but still shows signs of aliasing at higher frequencies.

Sample rate: $250\text{ MS/s}$:

Noise measurement comparisons at a sampling rate of $250\text{ MS/s}$: Top subplot shows the laser light input; middle subplot shows the blocked beam; bottom subplot displays the difference between raw and averaged traces. Due to the difference of around $5\text{ dB}$ between the averages of the traces, this sampling rate is identified as the minimum practical rate to avoid aliasing while maintaining manageable data size and processing speed.

Sample rate: $500\text{ MS/s}$:

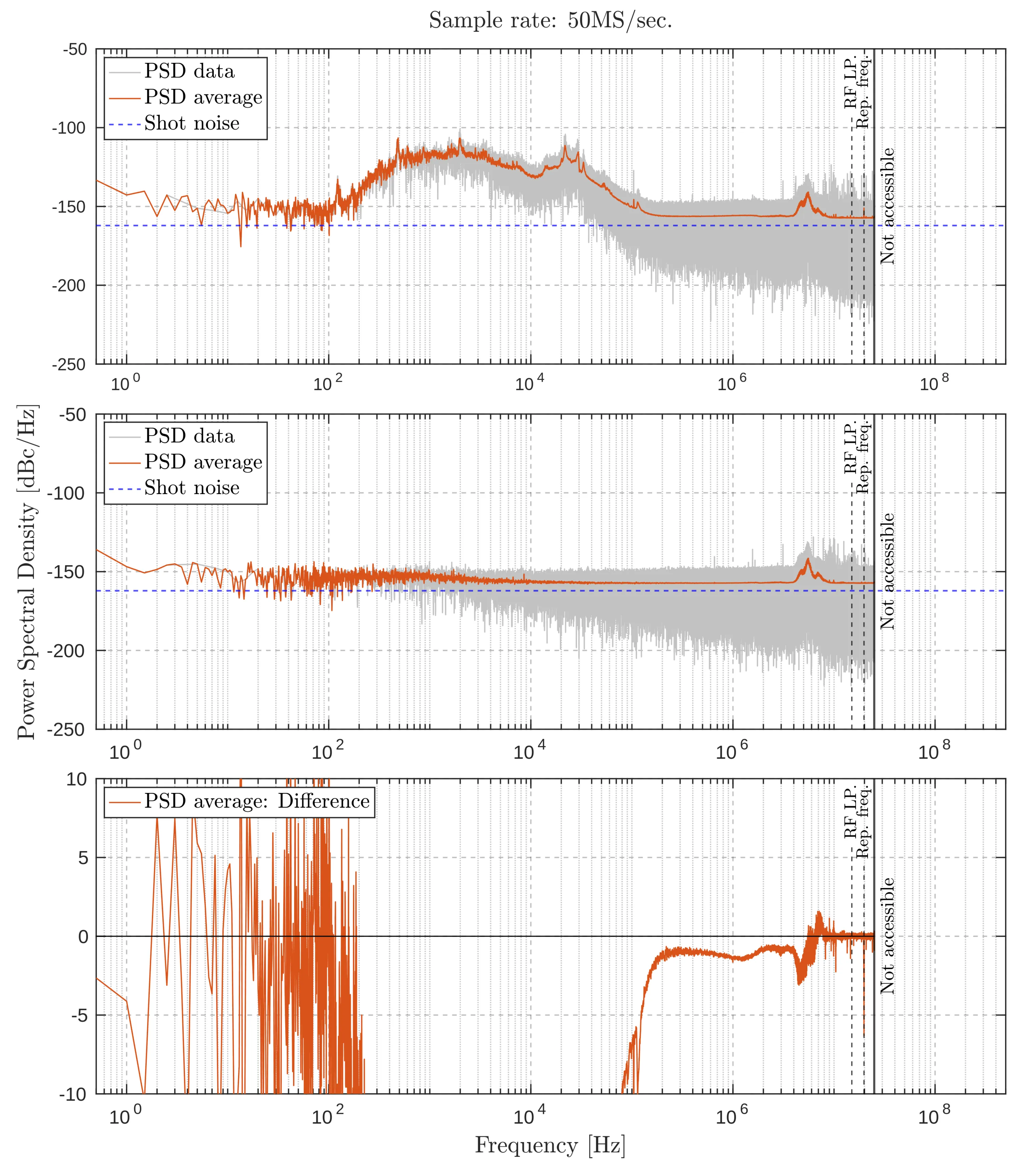
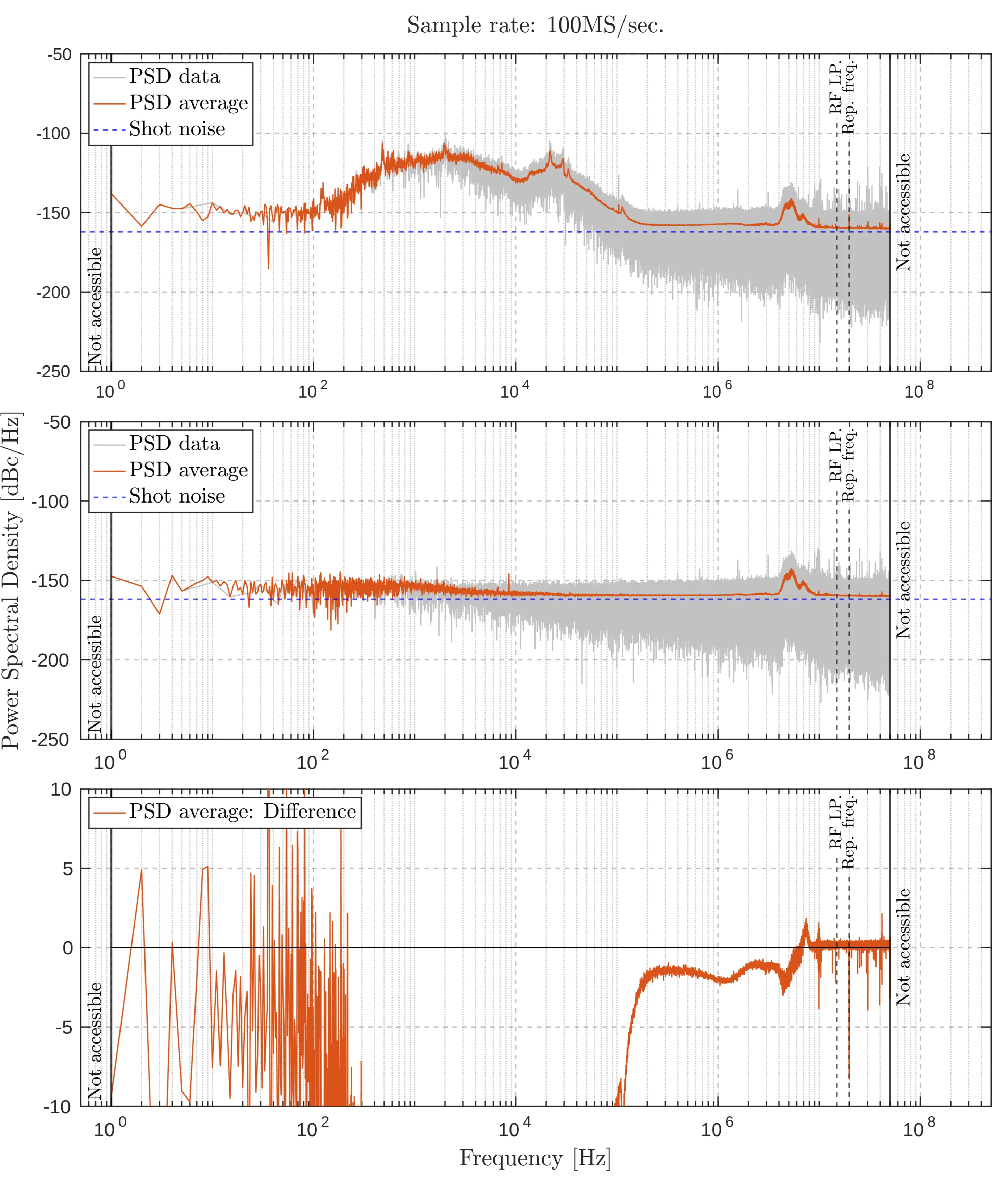
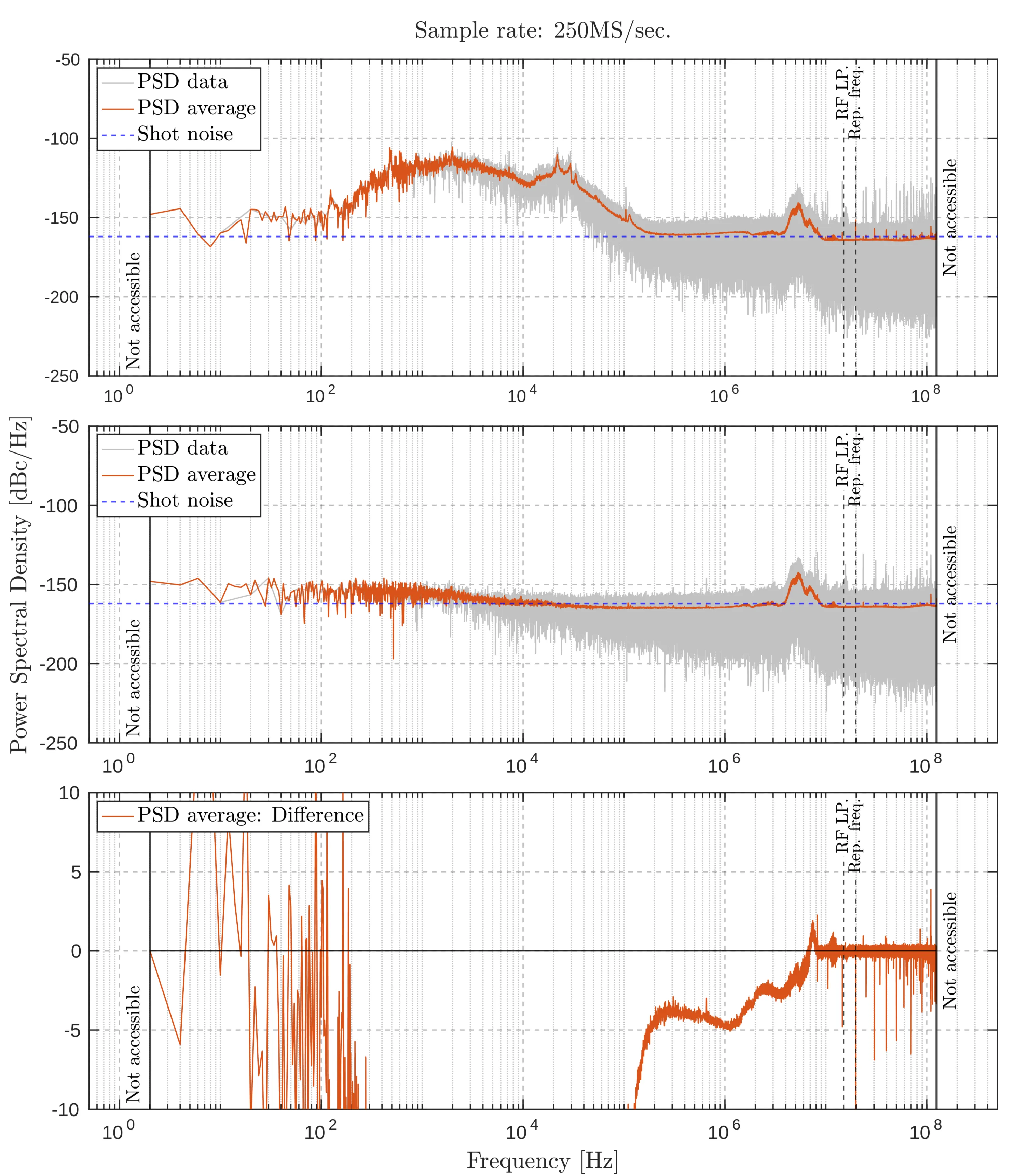
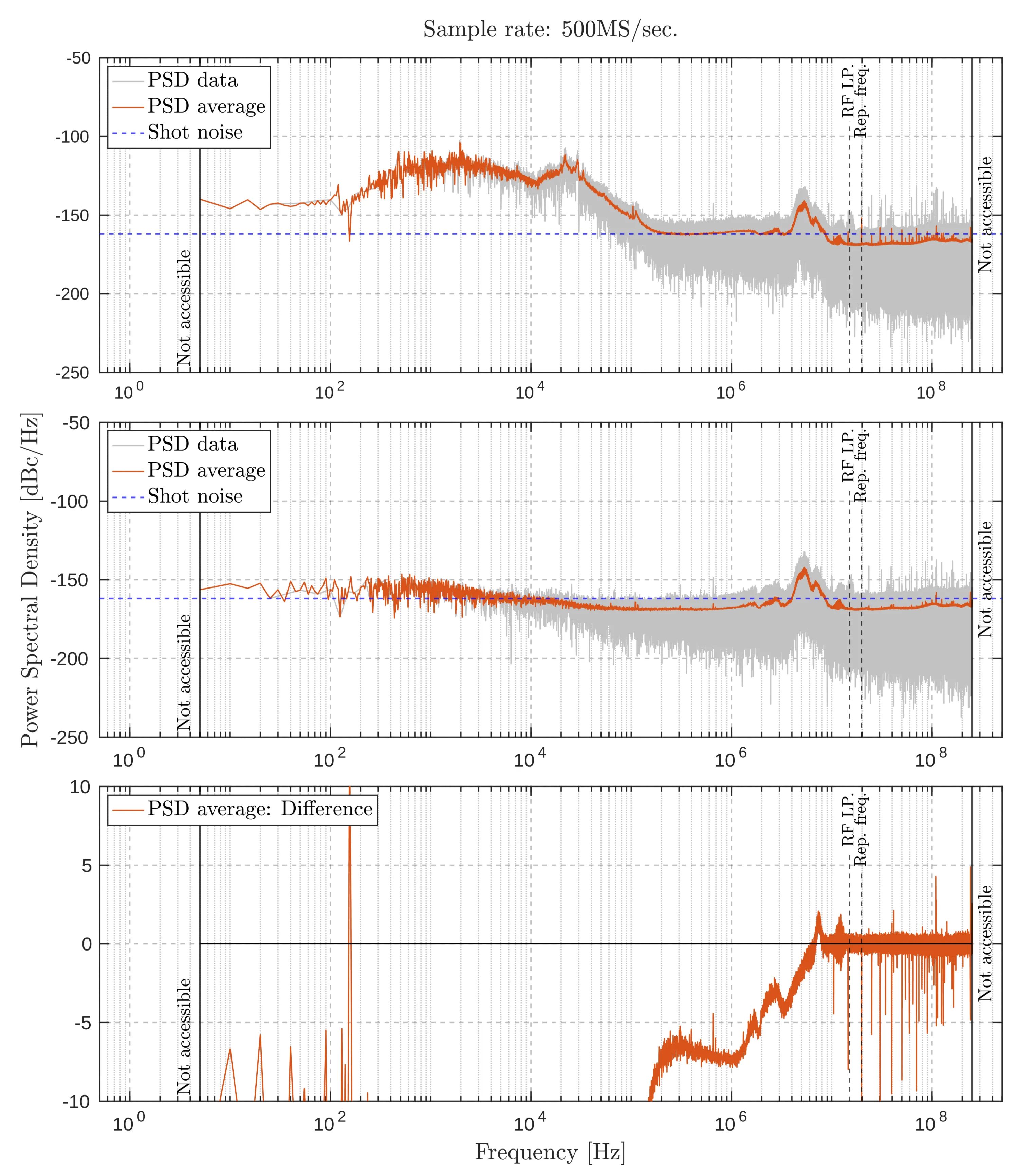
Noise measurement comparisons at a sampling rate of : Top subplot shows the laser light input; middle subplot shows the blocked beam; bottom subplot displays the difference between raw and averaged traces. Aliasing effects are further reduced at this sampling rate, though larger data size may limit measurement duration.

Sample rate $1\text{ GS/s}$:

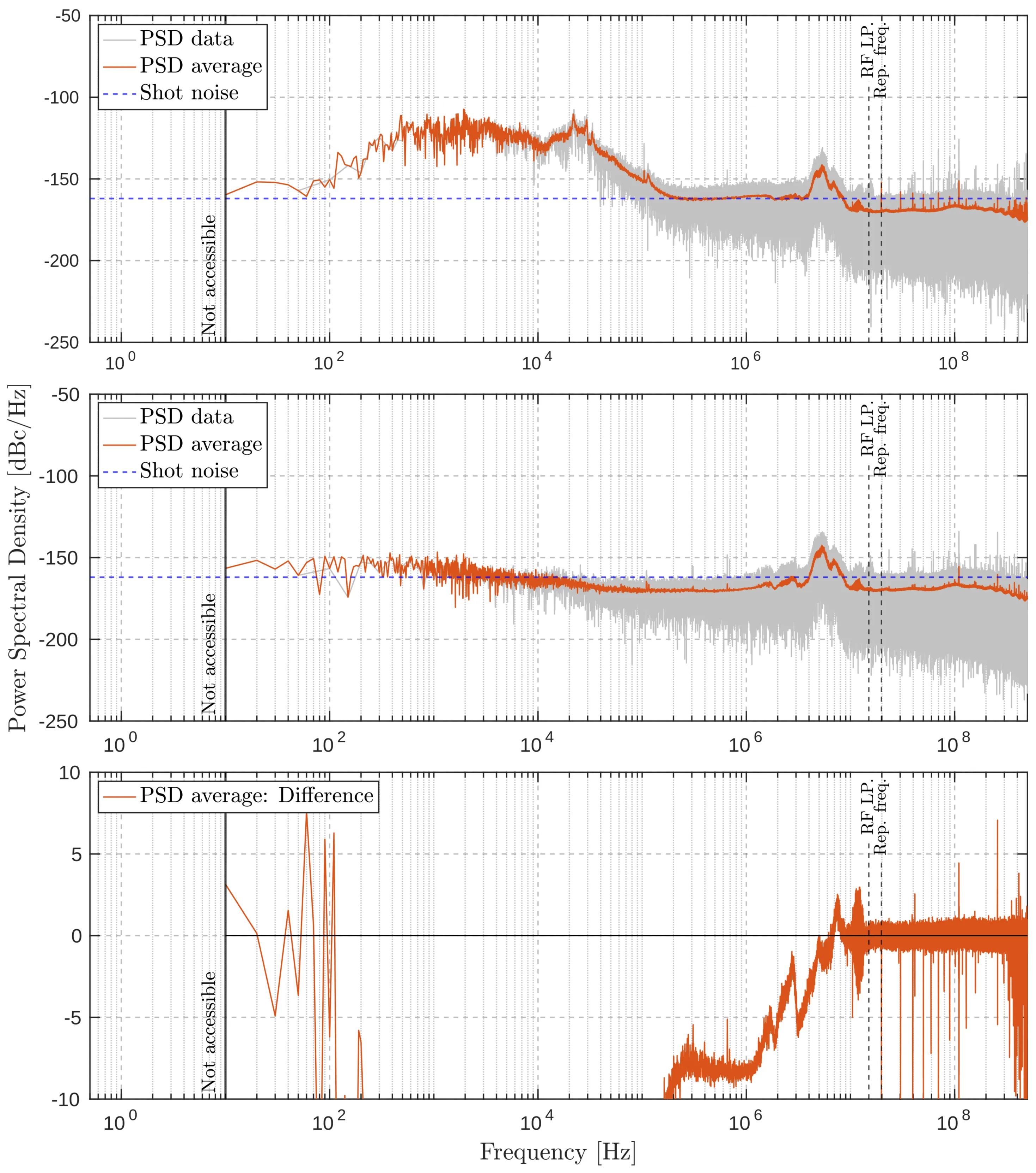
Noise measurement comparisons at a sampling rate of $1\text{ GS/s}$: Top subplot shows the laser light input; middle subplot shows the blocked beam; bottom subplot displays the difference between raw and averaged traces. The highest sampling rate provides the most accurate data but at the cost of reduced measurement duration due to data size limitations.

The results indicate that a sampling rate of $250\text{ MS/s}$ is the minimum practical rate to balance the need to avoid aliasing with manageable data size and processing speed. At lower rates, such as $50\text{ MS/s}$, the measured spectrum showed no meaningful data at $1\text{ MHz}$, as evidenced by the meagre difference between the traces, indicating inadequate signal capture. A noticeable difference between the traces was only observed at sampling rates of $250\text{ MS/s}$ or higher.

Note that each trace consists of exactly ${10}^8$ data points. The first trace, recorded with a sampling rate of $50\text{ MS/s}$, spans a duration of $2000\text{ ms}$, while the last trace, recorded at a sampling rate of $1\text{ GS/s}$, covers only $100\text{ ms}$. This consistent data size ensures that the results are directly comparable.

Because the x-axis is kept constant, the lowest possible frequency component is determined by the $50\text{ MS/s}$ sampling rate experiment, yielding $\frac{1}{2000\text{ ms}}=0.5\text{ Hz}$. The highest possible frequency component is dictated by the Nyquist-Shannon sampling theorem, which for the $1\text{ GS/s}$ trace is $\frac{1\text{ GS/s}}{2}=0.5\text{ GHz}$. Consequently, none of the previous experiments can access the full frequency range from $0.5\text{ Hz to }0.5\text{ GHz}$.

Resulting Noise Measurement

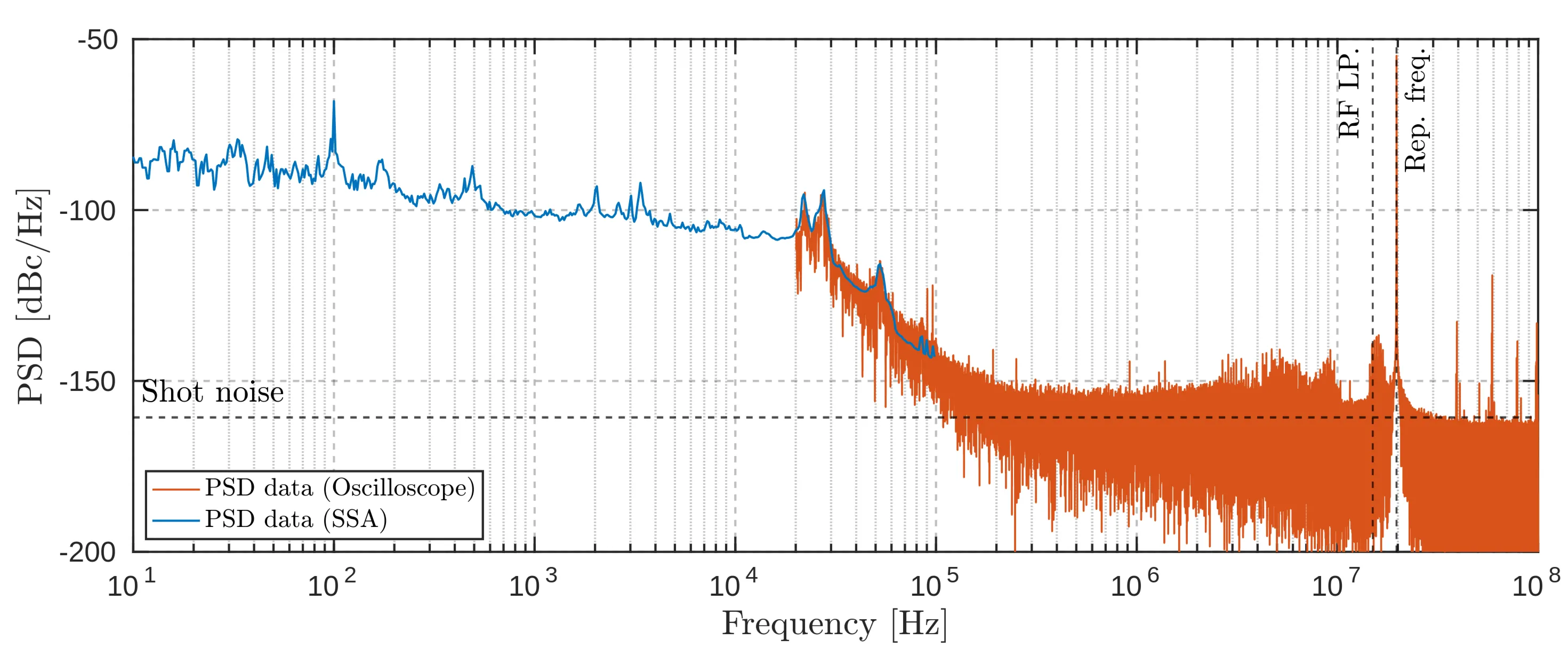
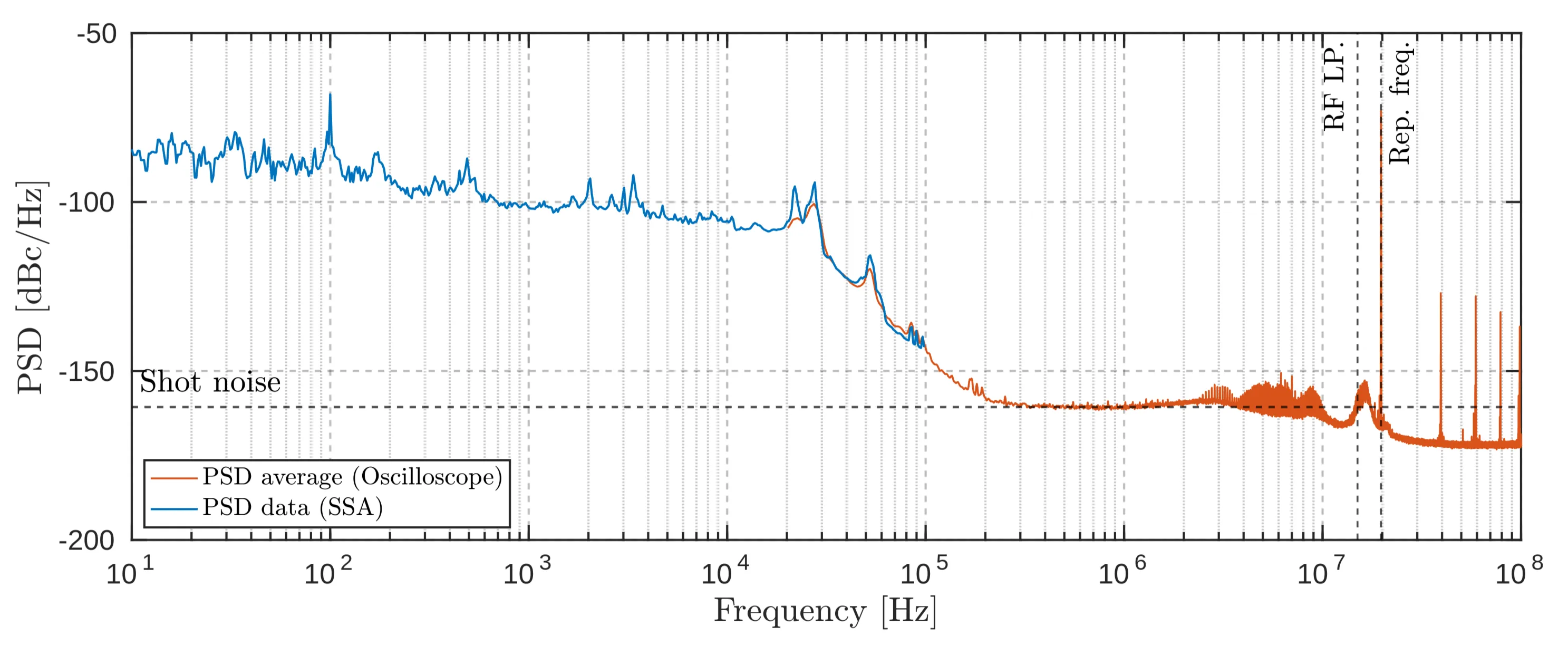
A good noise measurement can be conducted based on the preceding discussions and the collected data. Two traces were measured, one for each amplifier, and they overlapped in the frequency range from $20\text{ kHz to }500\text{ kHz}$ to determine the optimal stitching point. In the next figure, the result is shown.

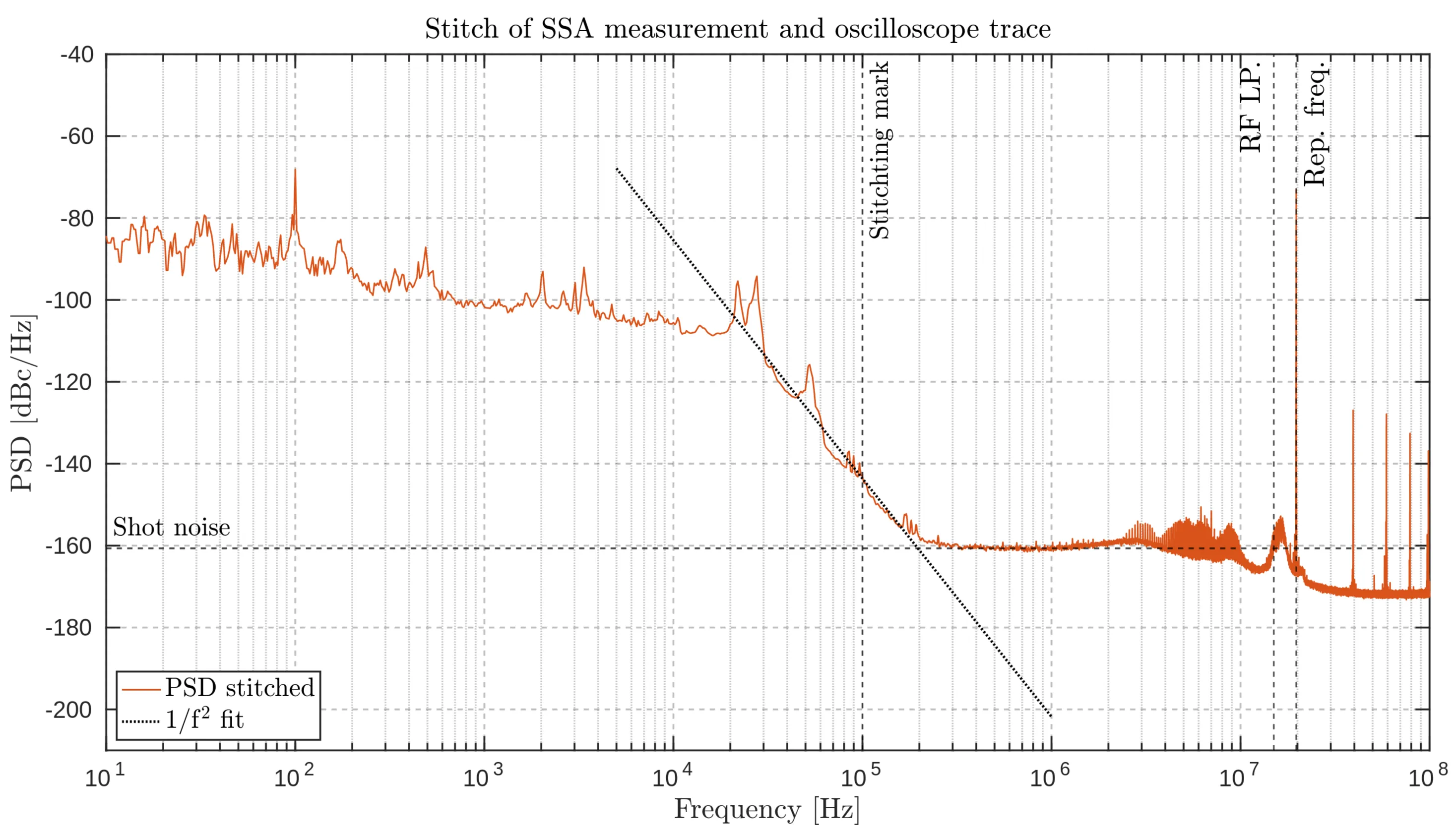
The blue trace is the noise PSD obtained from the SSA measurement, and the orange trace is the noise PSD obtained with the oscilloscope. As the oscilloscope operates with a finite sampling rate and measures for a finite time, it is unsurprising that the data appears very noisy. Therefore, it is impossible to draw any conclusions yet. To obtain visual clarity, the data has to be smoothed. This is done using Welch's method, as explained in the appendix. The resulting smoothed curve is depicted in the next figure, and now it can be seen that the noise curve runs into the shot-noise limit of $-162\text{ dBc/Hz}$ between $200\text{ and }300\text{ kHz}$. Further, it can be seen that the noise curves obtained from SSA and oscilloscope agree well in the overlapping region.

The stitching point is chosen as $100\text{ kHz}$, as the next figure shows. The orange curve shows the stitched noise PSD obtained from both measurements. A $1/f^2$ fit is applied to the region from $30\text{ to }200\text{ kHz}$ (in the $\log$ scale, this fit appears linearly and is shown for a wider frequency range). It can be seen that the fit approaches a value of a little lower than $-200\text{ dBc/Hz}$ at $1\text{ MHz}$ frequencies. Therefore, we expect the true laser noise to run into the shot-noise limit at $1\text{ MHz}$. The offset between the curves, or the stitching error, is virtually zero.

3.6 Technical Considerations

In this section, technical considerations are addressed, and while not directly related to the core research, they are crucial for successful experimentation. These practical aspects can often become sources of frustration in the lab, as they are necessary but can be more challenging than anticipated. By sharing these insights, I hope to shed light on some of the unexpected daily challenges that can arise and potentially delay progress in the project.

As previously mentioned, most of the laser's power will be directed into a hollow-core photonic crystal fibre (HCPCF), where the spectral broadening will occur. Given that this power is approximately $50\text{ W}$, several precautions are necessary to prevent damage to the fibre. Additionally, the photodiode used for noise measurement must be actively protected, as small spectral drifts could significantly increase the incident power, posing a risk of damaging the photodiode.

The HCPCF is integrated with GLOphotonic's Powerlink system, which offers a comprehensive solution allowing for pressures up to $30\text{ bar}$, $50\text{ W}$ average input power, and water-cooling at the input side, all while maintaining a transmission efficiency of $>85\mathrm{\%}$. The fibre has a specified mode-field diameter (MFD) of $42\mu \text{m}$, necessitating precise beam collimation to match this size. However, improper positioning or angling of the laser beam can cause immediate and irreversible damage to the fibre, making active beam stabilisation crucial.

3.6.1.1 Beam Stabilisation

An active laser beam stabilisation system from MRC is employed to achieve the required precision, utilizing a combination of two 4QD detectors and two controllable mirrors, referred to as actuators. The next figure illustrates the setup schematically.

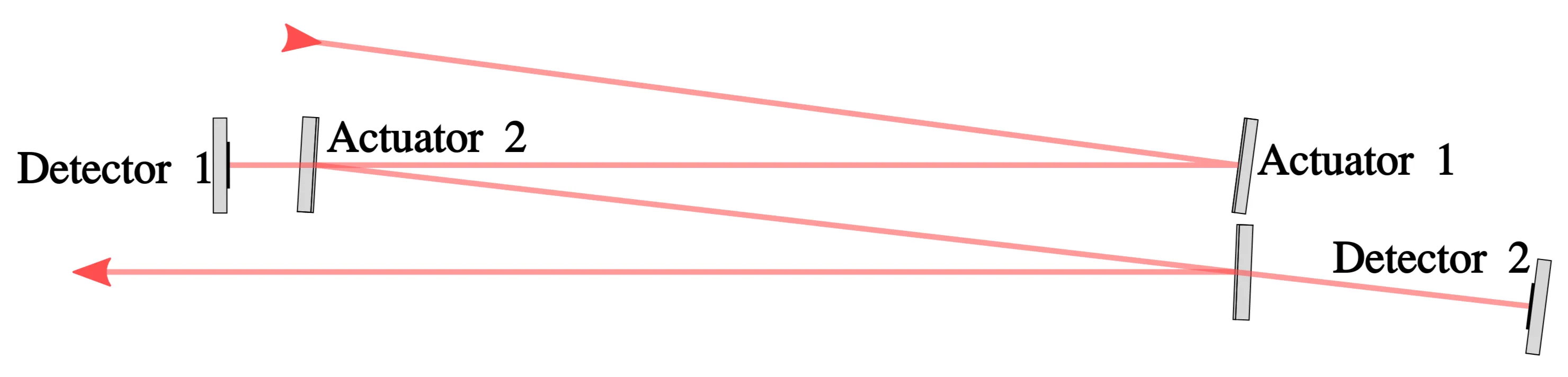
Schematic of the beam stabilisation setup. The system utilises two 4QD detectors and two actuators to stabilise the laser beam actively. Detector 1 receives input from the leakage of actuator 2, while detector 2 receives input from a subsequent mirror. The detectors continuously adjust the actuators to maintain the beam's position, compensating for any fluctuations in beam-pointing and ensuring precise alignment.

After being reflected by actuator 1, the laser beam reaches actuator 2, which then reflects it to the subsequent mirror. The movement of actuator 1 is controlled by detector 1, which receives input from the leakage of the mirror in front of actuator 2. Both detectors adjust their corresponding actuators to ensure the signal remains centred on their four photodiodes. This configuration compensates for beam-pointing fluctuations, thereby minimising variations in beam position and angle.

To verify the effectiveness of the stabilisation system, the fluctuations in beam position were compared with the stabilisation system turned on and off. The next figure compares the unstabilised and stabilised horizontal and vertical positions.

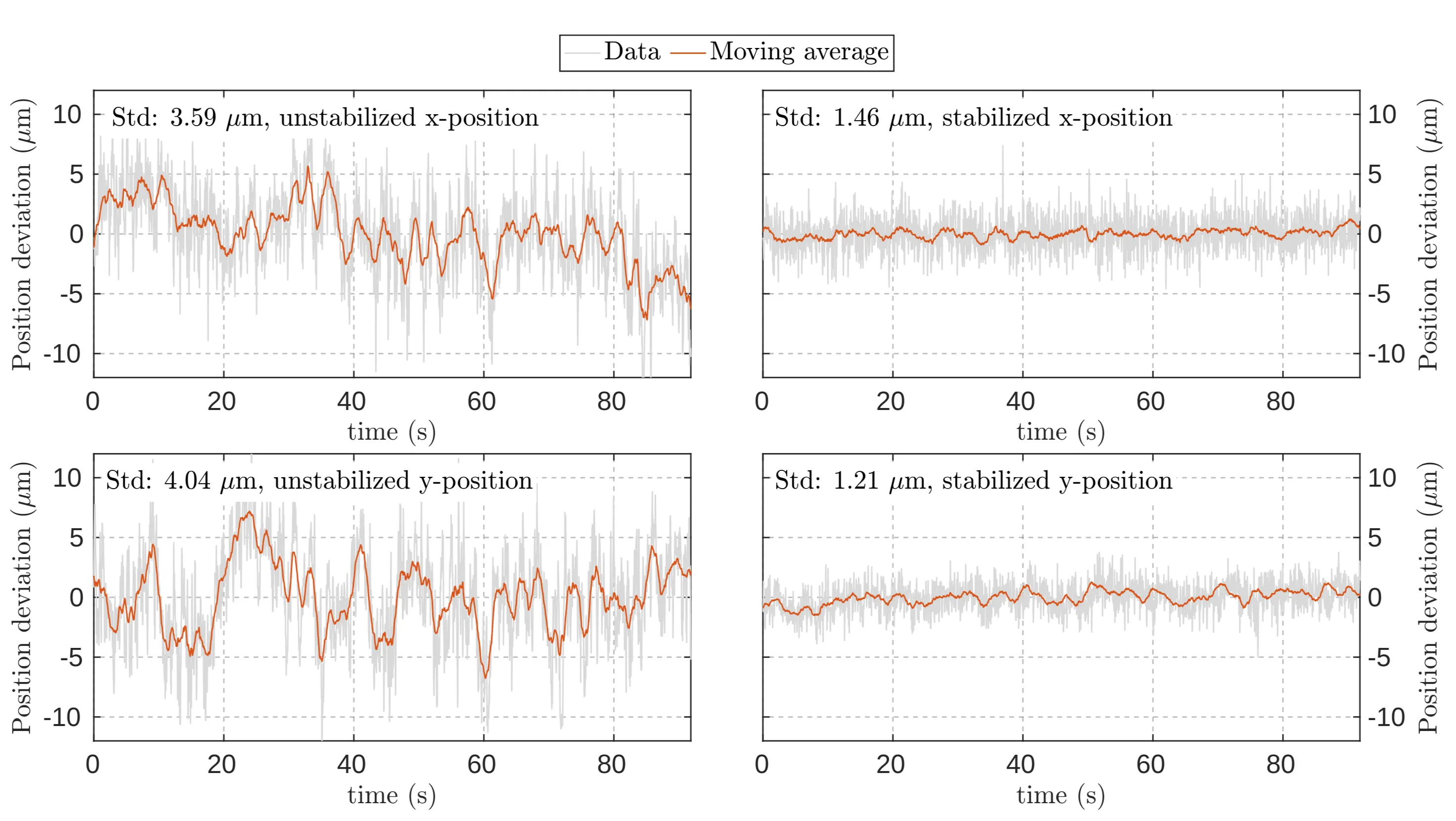
Comparison of beam position fluctuations in both $x$ and $y$ directions with and without active stabilisation. The plots on the left show the fluctuations without stabilisation, while the plots on the right show the reduced fluctuations with stabilisation applied. The standard deviation for each case is indicated within the plots, demonstrating the effectiveness of the stabilisation system in minimising beam drift. The moving average is each over 30 data points, averaging over $1.3\text{ seconds}$.

As shown, the beam stabilisation reduces the positional standard deviation from $3.59\mu \text{m}$ and $4.04\mu \text{m}$ to $1.48\mu \text{m}$ and $1.21\mu \text{m}$, respectively, for the uncollimated beam. This demonstrates that the laser beam fluctuations have been minimised to a safe level for directing the full signal into the fibre without causing damage. When we initially directed more than $5\text{ W}$ of power into the fibre, the laser occasionally shut down unexpectedly, triggering the interlock without an apparent cause. The issue was traced to the reflection of the fibre facet, which created a secondary light spot on the detectors. This caused the detectors to incorrectly interpret the beam position as outside their operational range. A straightforward solution was moving the detector away from the leaking mirror, ensuring the back-reflection bypassed the detector's sensitive area.

3.6.1.2 Interlock: Pump Diode

When the active laser beam stabilisation system functions correctly, the laser beam couples into the fibre as intended. However, if there are significant drifts in the beam path, the beam position may move outside the working range of the actuators, rendering them unable to compensate for the misalignment. In such cases, the detectors may detect insufficient power, causing the actuators to default to a "zero position," which leads to the stabilisation system shutting down. If the beam is accidentally blocked or the control system loses power, the piezo motors drive the actuators to an extreme position. Both scenarios risk damaging the fibre and other optical components, making manual laser shutdown too slow to prevent potential damage. To address this, an interlock system has been implemented. Under normal operating conditions, the interlock circuit of the laser pump diode remains closed, allowing the pump laser to continue pumping the TDL gain medium. However, if any of the scenarios above occur, the circuit is opened, immediately stopping the pump diode and shutting down the laser. While this process is not instantaneous, it significantly reduces the risk of damage. The control system outputs a $5\text{ V}$ signal when everything is functioning correctly or if the system has not been activated. Still, no signal is sent when the actuators are in the zero or extreme position, effectively serving as a TTL signal. This setup is easily managed using a solid-state relay (SSR). We initially experimented with MOSFETs and optocouplers, but they struggled to handle the $24\text{ V}$ present between the interlock pins. The SSR proved ideal, as it can handle load voltages up to $230\text{ V}$.

However, in this configuration, the laser would never turn on because the beam stabilisation cannot function without an active laser, and the pump diode cannot be activated without beam stabilisation. To resolve this, a simple override switch was added to the system. The override temporarily bypasses the interlock, allowing the laser to turn on and the beam stabilisation to operate. Once the stabilisation is operational, the override switch is deactivated. The response time between the low TTL signal and the pump diode reaction is expected to be within the millisecond range, although it has not been explicitly measured. This interlock system provides the fastest safety mechanism to be implemented with relative ease and minimal complexity.

With this system in place, the only light that could potentially damage the fibre or other optical components after an error is detected is the residual light already oscillating within the cavity.

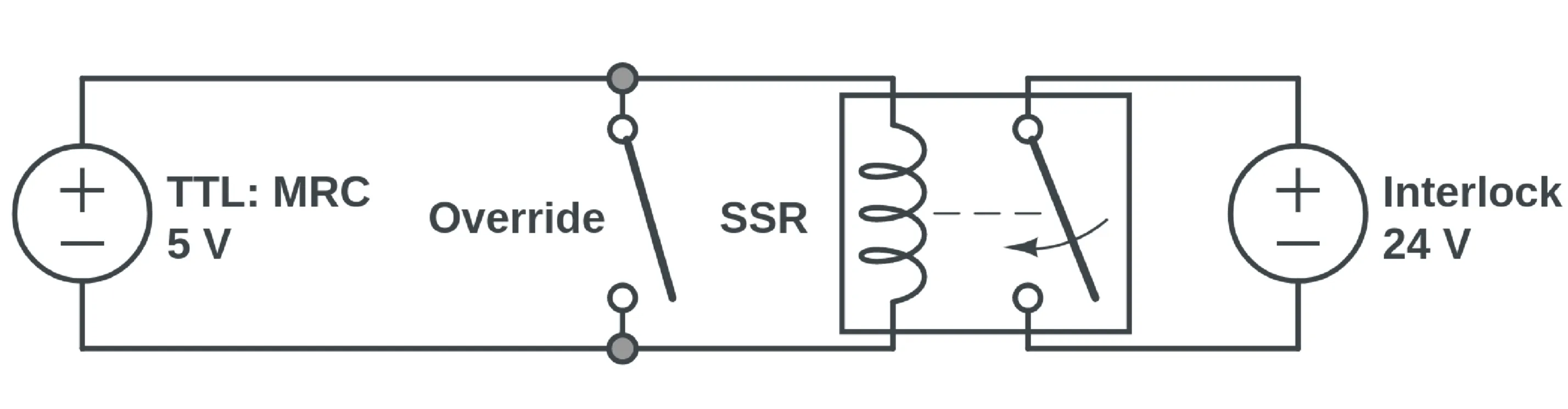
Electrical circuit of the pump diode interlock system, illustrating the components involved in safeguarding the laser setup. The circuit includes a $5\text{ V}$ TTL voltage source, an override switch, a solid-state relay (SSR), and a $24\text{ V}$ interlock. This configuration ensures that the pump diode is shut down in case of beam misalignment or stabilisation failure, preventing potential damage to the fibre and optical components. The override switch allows for a controlled startup sequence, temporarily bypassing the interlock to activate the laser and stabilisation system.

3.6.1.3 Interlock: Photodiode

After the light exits the fibre, it passes through a grating spectrometer, which allows for the selection of a specific wavelength range of the spectrum using a narrow slit. As shown in chapter 2.6.4, the power within a $1\text{ nm}$ slice of the spectrum can reach up to $3\text{ W}$. However, since the high-gain region typically exhibits lower power levels, this is the area where we aim to conduct the noise measurement using the photodiode. The challenge arises when the selected spectral slice shifts slightly, potentially moving into a region with higher power per nanometre. This shift could significantly increase the incident power on the photodiode, risking its destruction. To mitigate this risk, a second photodiode operating at a power level below the maximum incident power is used, which still ensures a linear voltage response. In the event of a spectral shift, the incident power on both photodiodes will increase. However, before the power reaches a level that could damage the noise-measuring photodiode, the second photodiode will trigger a warning that blocks the light. This interlock system is effective for gradual drifts, a conclusion supported by testing the setup over several hours of laser operation. The second photodiode generates a voltage signal serving as input to an MKRzero Arduino, functioning as an analog-to-digital converter (ADC). By defining an appropriate threshold voltage, the system controls a rotation mirror mount equipped with a D-shaped mirror. Depending on whether the voltage exceeds or falls below the threshold, the mirror rotates by ${180}^{\circ }$, effectively blocking or allowing the light to continue.

3.7 Full Setup

The next figure provides a schematic overview of the experimental setup. This illustration includes key components such as active beam stabilisation, power and polarisation control, water cooling, and the grating spectrometer. The laser cavity, noise measurement, and diagnostic elements are represented schematically.

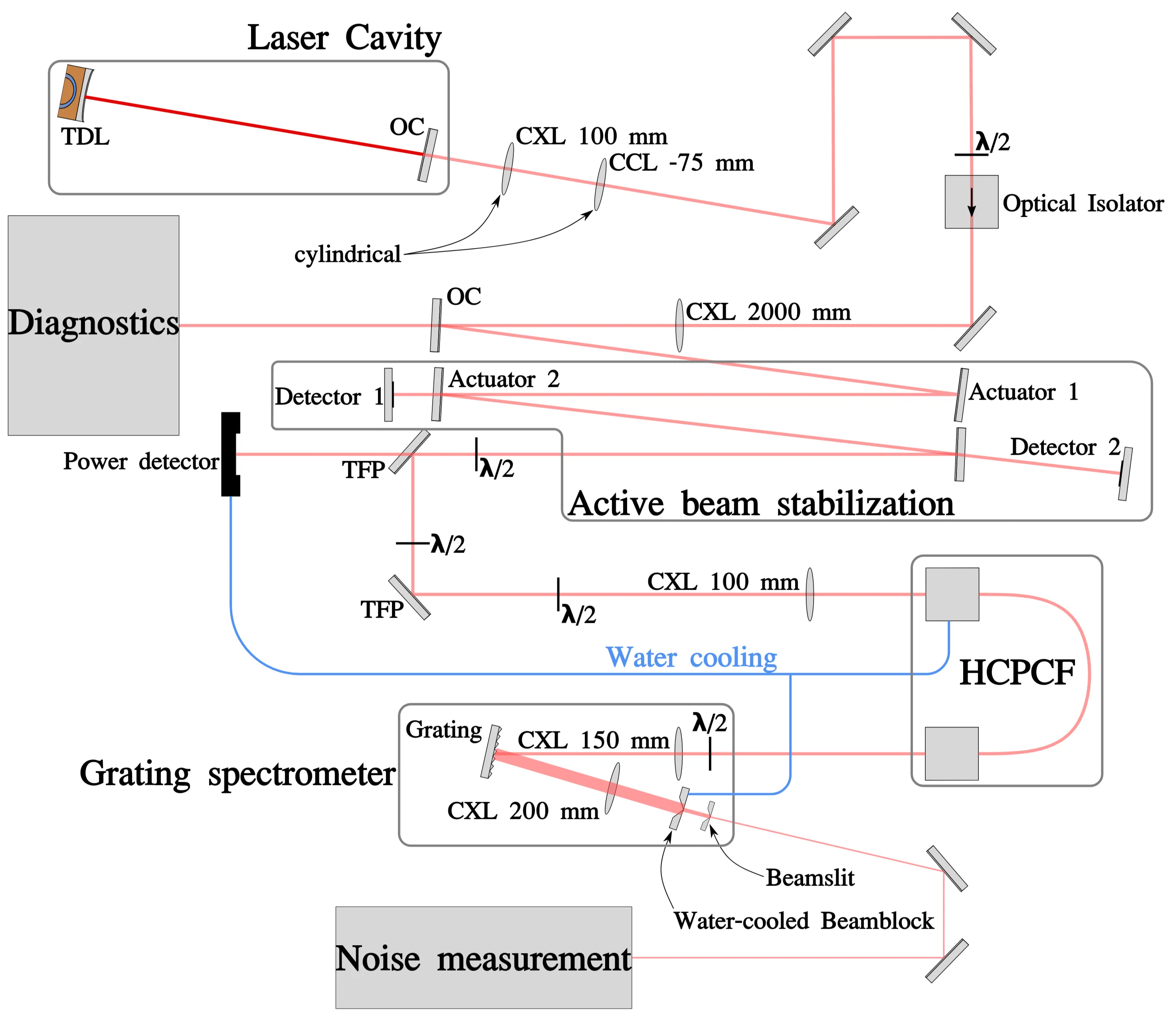
Schematic of the complete experimental setup, highlighting the active beam stabilisation, power and polarisation control, water cooling, and the grating spectrometer (distances not to scale). The laser cavity, noise measurement, and diagnostic components are shown schematically. CXL: convex lens, CCL: concave lens, $\lambda /2$: half-wave plate, OC: output coupler, TFP: thin-film polariser, HCPCF: hollow-core photonic crystal fibre.

The next image shows the cavity as seen in the lab.

The final laser cavity as seen in the laboratory. The dark red path traces the laser light oscillating in the cavity, while the bright red shows the outcoupled light, indicating that the output power is $10\mathrm{\%}$ of the intracavity power.