Jump back to chapter selection.

Table of Contents

9.1 Poincaré Sphere and Stokes Vector
9.2 Jones Vector Formalism
9.3 Anisotropic Materials
9.4 Optical Activity
9.5 Magneto-Optics
9.6 Electro-Optics

9 Polarisation Optics

As described earlier, a basic property of light is its polarisation. There are several different ways to describe the polarisation state of light. Here we will discuss three of the more common formalisms: the Poincaré sphere, the Stokes parameters, and the Jones vector formalism.

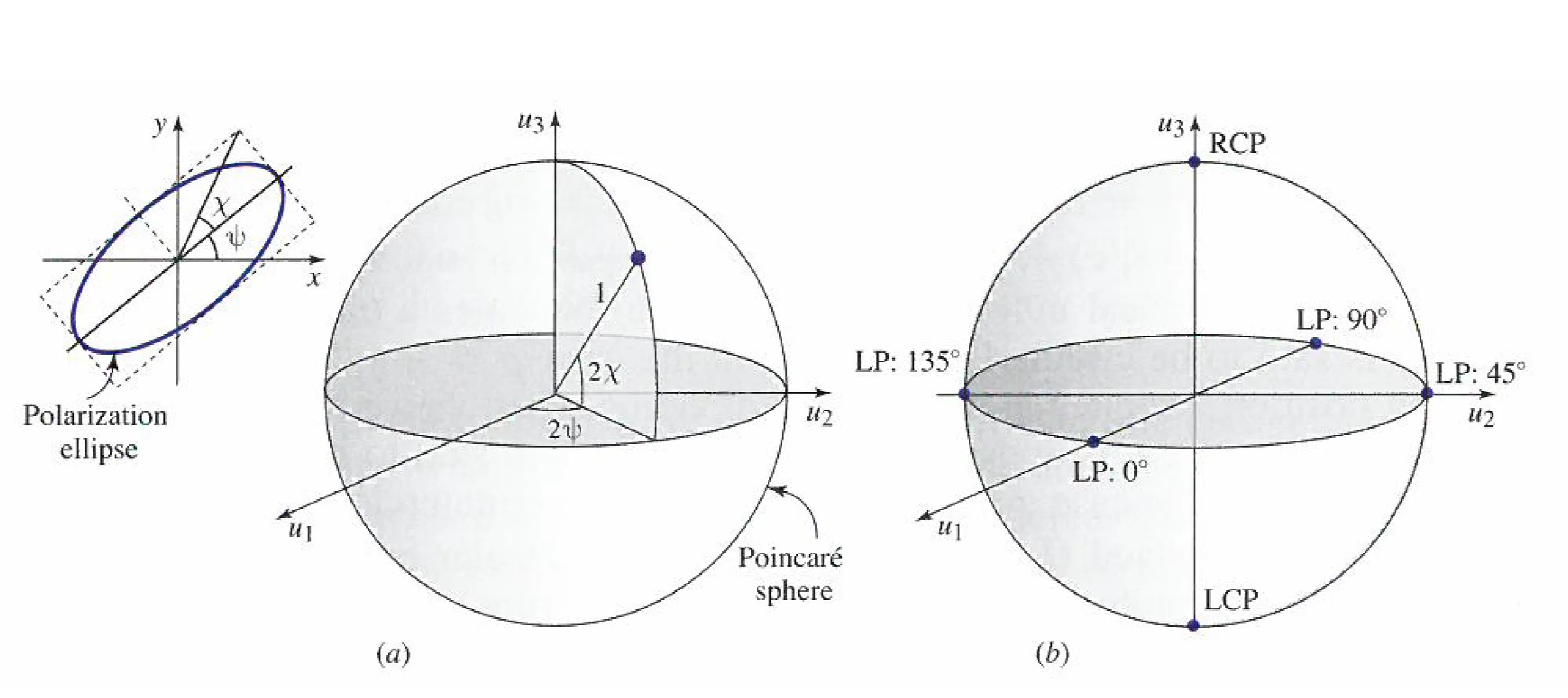
9.1 Poincaré Sphere and Stokes Vector

Let us assume that we have a plane wave propagating in the $+z$ direction in free space. Using complex notation, the transverse electric field components ${\mathcal{E}}_x$ and ${\mathcal{E}}_y$ can be written at a specific point (say, $z=0$) as a function of time:

where $a_x,a_y,{\varphi }_x,$ and ${\varphi }_y$ are real constants representing the amplitudes and initial phases of the $x$ and $y$ components, respectively. The real, physical electric field components are then:

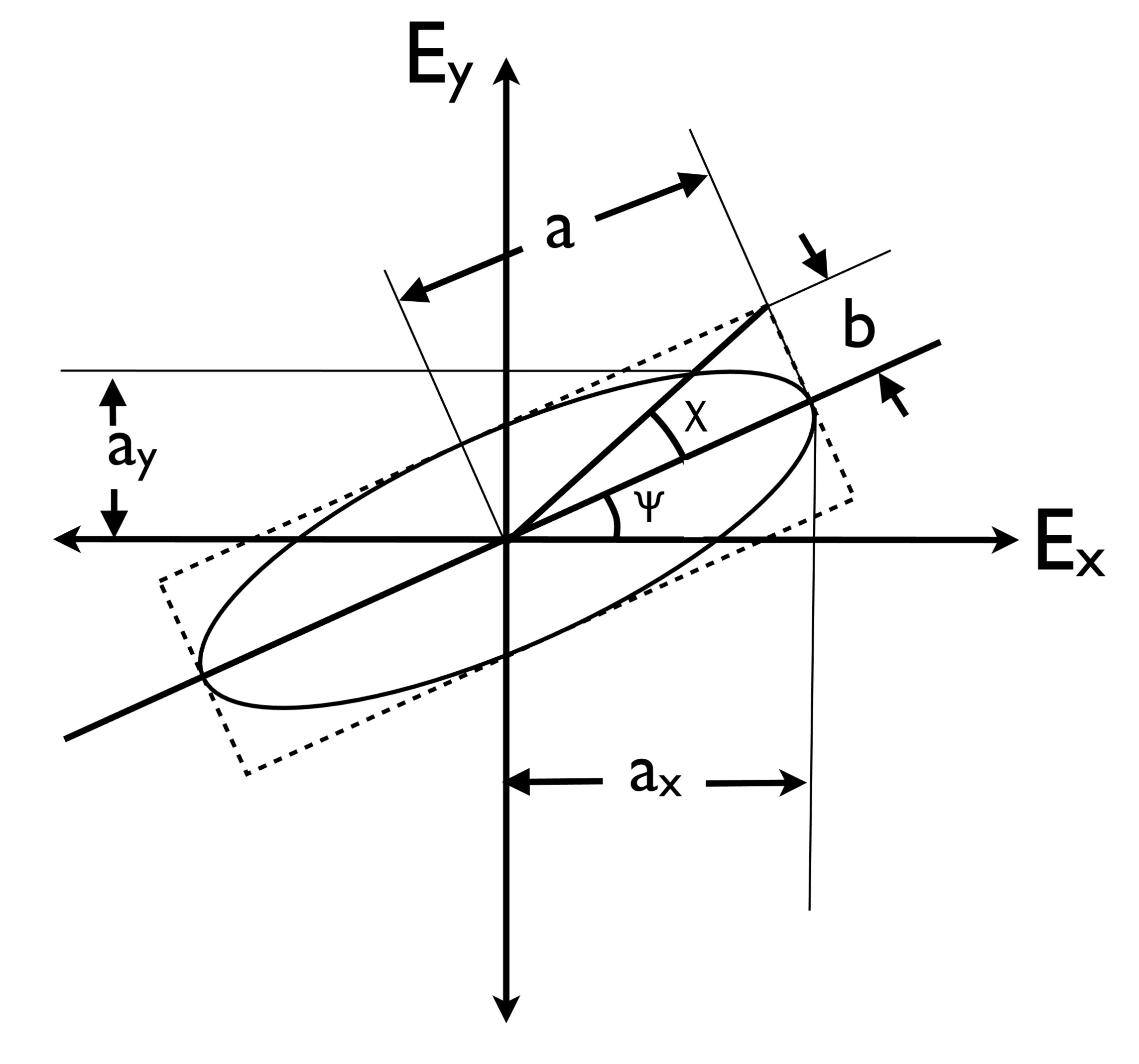
These are parametric equations describing an ellipse in the $xy$-plane as time evolves, known as the polarisation ellipse:

where $\varphi ={\varphi }_y-{\varphi }_x$ is the relative phase difference. This is depicted in the following figure:

The shape and orientation of this ellipse can be characterised by two angles: an orientation angle $\psi$ (the angle of the major axis of the ellipse with respect to the $x$-axis) and an ellipticity angle $\chi$ (where $\tan |\chi |$ is the ratio of the semi-minor to semi-major axes). These are given by:

The sign of $\chi$ indicates the handedness of the polarisation: positive $\chi$ for right-handed elliptical polarisation (clockwise rotation of $\mathbf{E}$ when looking towards the source, by one convention) and negative $\chi$ for left-handed. These two angles, $2\psi$ (longitude, ranging from $0$ to $2\pi$) and $2\chi$ (latitude, ranging from $-\pi /2$ to $\pi /2$), uniquely define a point on the surface of a sphere of unit radius, known as the Poincaré sphere. Each point on the sphere represents a distinct polarisation state.

Linear polarisations lie on the equator of the Poincaré sphere ($2\chi =0$). Right-circular polarisation corresponds to the north pole ($2\chi =\pi /2$), and left-circular polarisation to the south pole ($2\chi =-\pi /2$). The Poincaré sphere describes only the polarisation state, not the overall intensity of the light.
Another representation, which includes intensity information, is the set of Stokes parameters:

These parameters are not all independent. For fully polarised light, $S_0^2=S_1^2+S_2^2+S_3^2$. For partially polarised light, $S_0^2\ge S_1^2+S_2^2+S_3^2$. The Stokes parameters $S_1,S_2,S_3$ can be viewed as Cartesian coordinates of a point on or inside the Poincaré sphere (if normalised by $S_0$), thus providing an equivalent description of polarisation state, while $S_0$ gives the total intensity.

9.2 Jones Vector Formalism

Another powerful way to describe fully polarised light is using the Jones vector, a two-component complex vector representing the amplitudes and phases of the $x$ and $y$ components of the electric field:

where the common $e^{i\omega t}$ factor is omitted. This vector completely specifies the polarisation state and amplitude of the light field at a particular point. Some examples include:

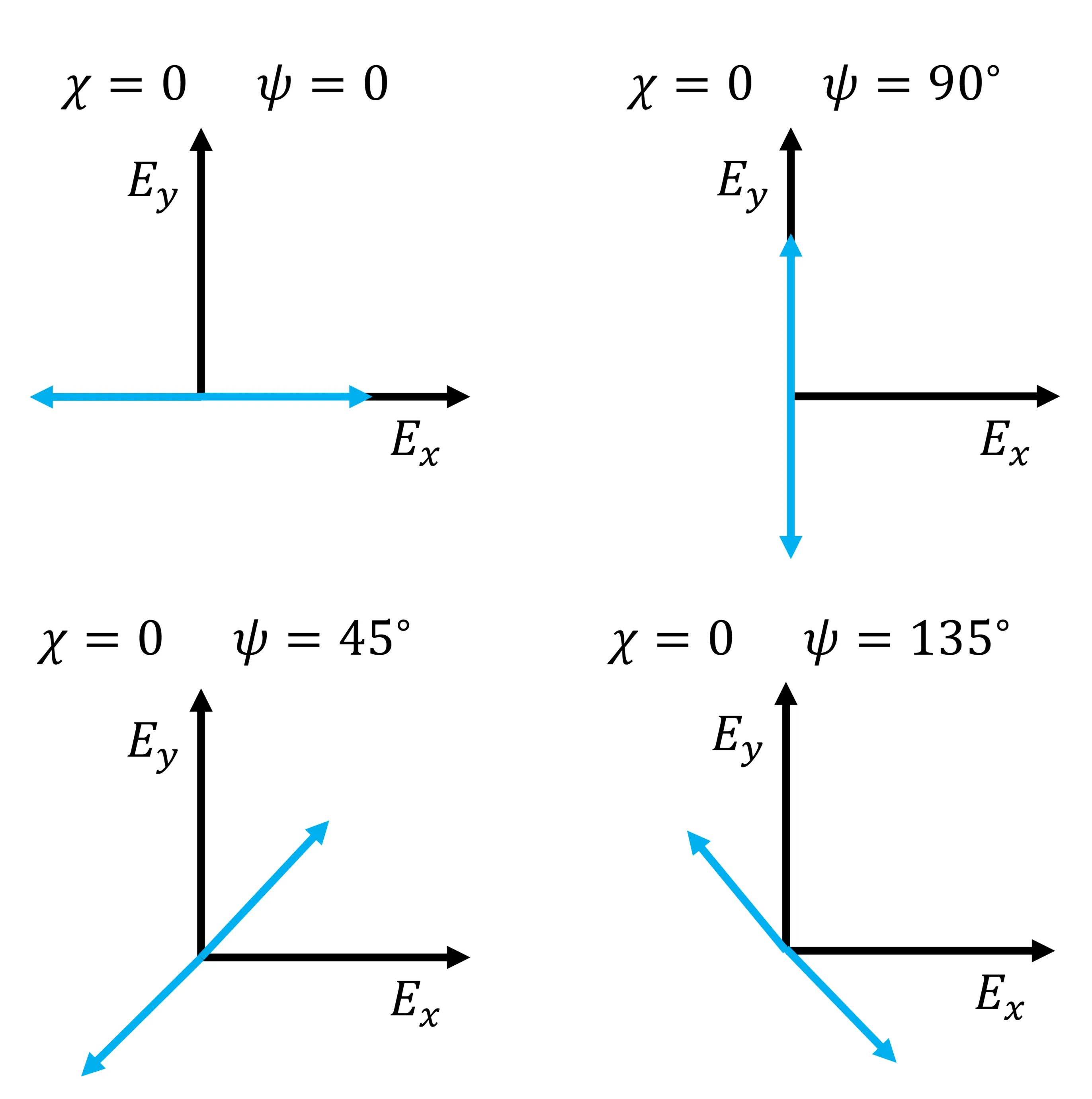
• Linearly polarised light along x: $\mathbf{J}=\left(\begin{array}{c}1\\ 0\end{array}\right)$ (amplitude normalised)
• Linearly polarised light along y: $\mathbf{J}=\left(\begin{array}{c}0\\ 1\end{array}\right)$
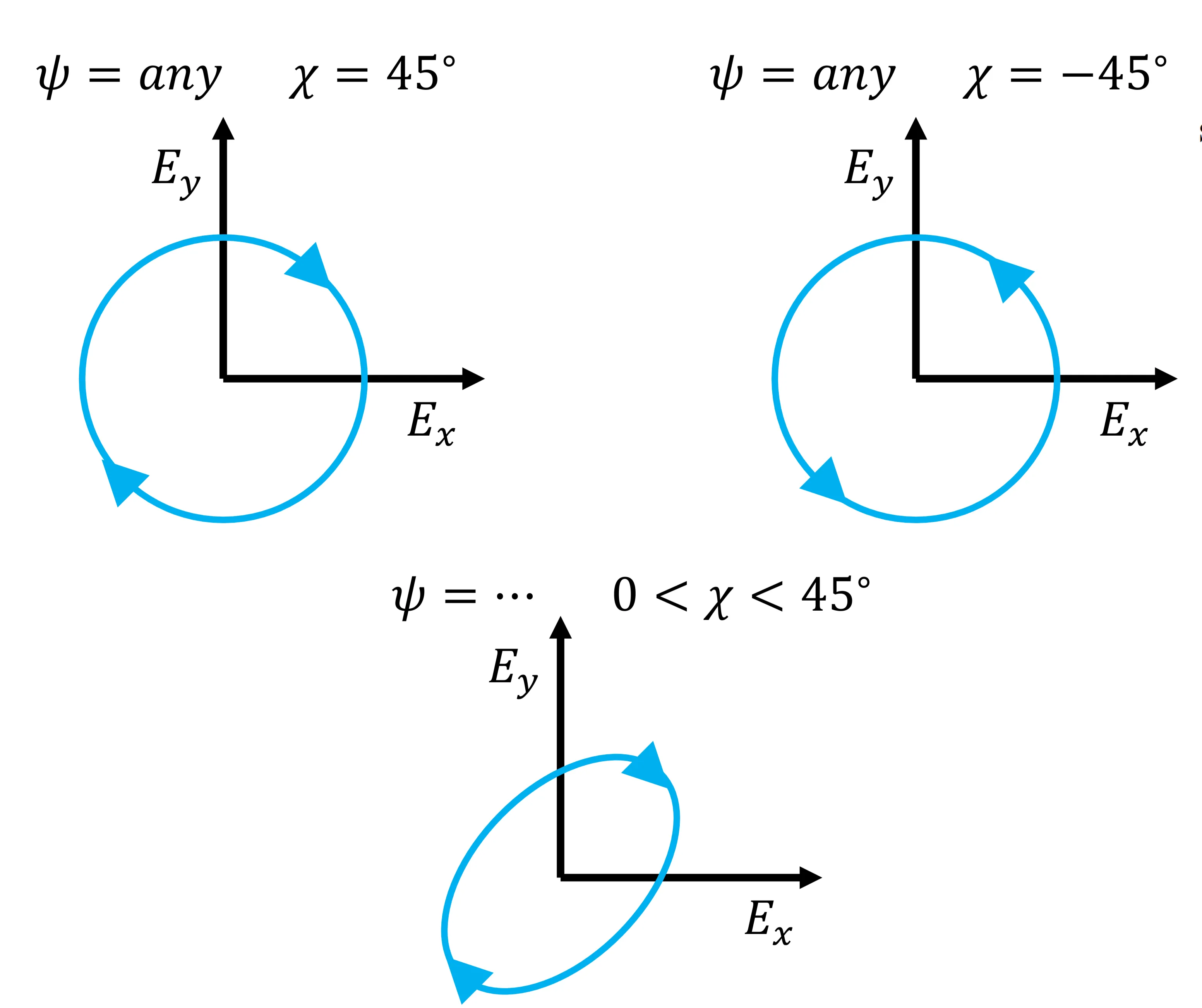
• Right-circularly polarised light: $\mathbf{J}=\frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\ i\end{array}\right)$ (by one convention, where $E_y$ leads $E_x$ by $\pi /2$)
• Left-circularly polarised light: $\mathbf{J}=\frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\ -i\end{array}\right)$

Two states of polarisation represented by Jones vectors ${\mathbf{J}}_1$ and ${\mathbf{J}}_2$ are orthogonal if their inner product is zero:

Examples of orthogonal polarisation states are x- and y-linearly polarised light, or right- and left-circularly polarised light. Any Jones vector can be represented as a linear combination of two orthogonal Jones vectors (which form a basis).

The utility of this formalism lies in describing the action of optical devices that alter the polarisation state or intensity of light using $2\times 2$ complex matrices, known as Jones matrices. If the input polarisation is described by ${\mathbf{J}}_{\text{in}}$, the output polarisation ${\mathbf{J}}_{\text{out}}$ after passing through an optical element with Jones matrix $\mathbf{T}$ is:

Some examples of Jones matrices for common optical elements:

• Linear polariser passing $x$-polarised light (and blocking $y$-polarised light):$${\mathbf{T}}_{\text{LP,x}}=\left(\begin{array}{cc}1& 0\\ 0& 0\end{array}\right)$$
• Wave retarder (wave plate): Introduces a phase shift $\mathrm{\Gamma }$ between two orthogonal linear polarisation components. If the $x$-axis is the fast axis (lower refractive index) and the $y$-axis is the slow axis (higher refractive index), the matrix is:$${\mathbf{T}}_{\text{ret}}=\left(\begin{array}{cc}1& 0\\ 0& e^{-i\mathrm{\Gamma }}\end{array}\right)$$where $\mathrm{\Gamma }=(n_s-n_f)k_{0}d$ is the retardance ($n_s,n_f$ are slow/fast refractive indices, $d$ is thickness).
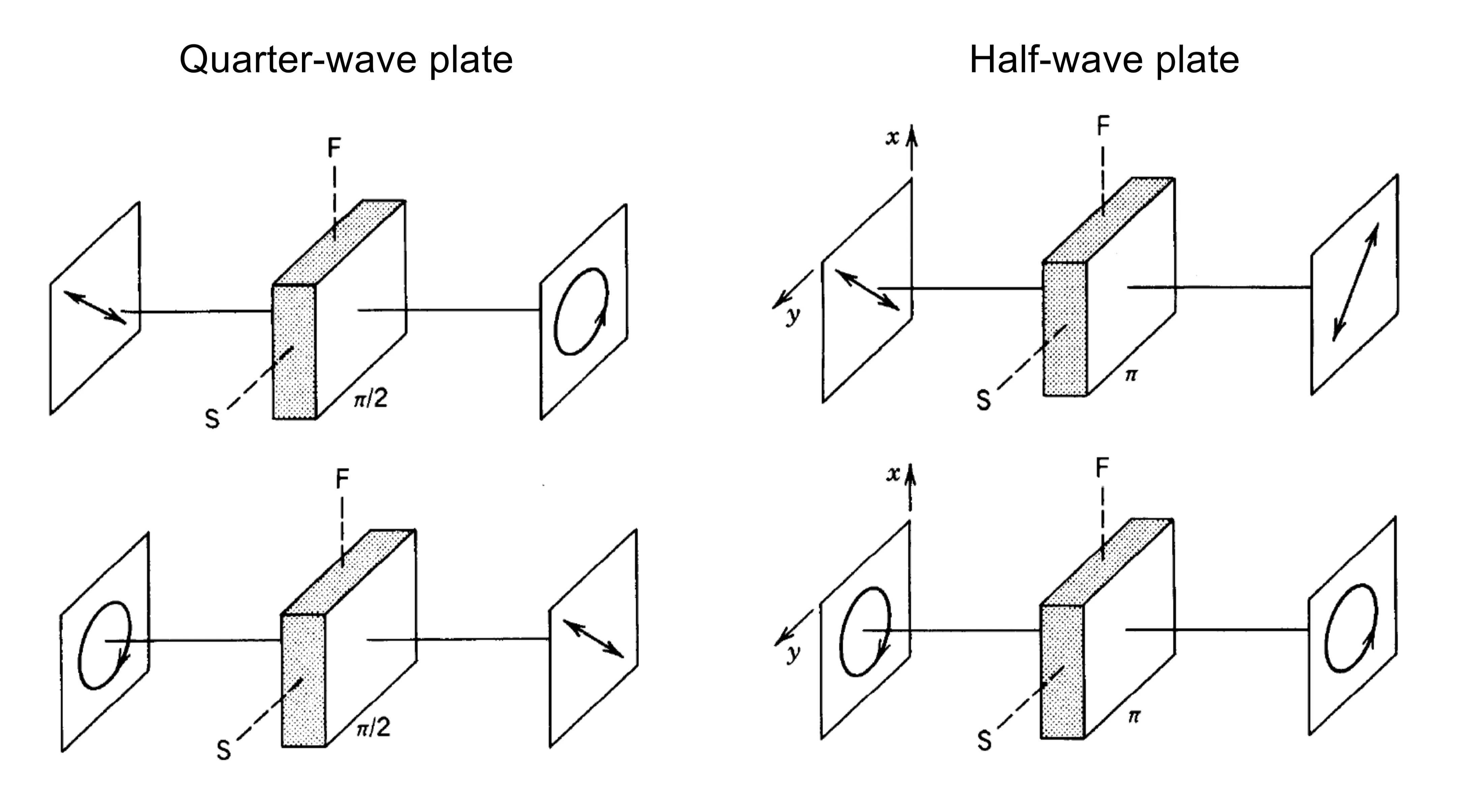
  • For $\mathrm{\Gamma }=\pi /2$, it is a quarter-wave plate. It can convert linearly polarised light (at ${45}^{\circ }$ to its axes) to circularly polarised light, and vice versa.
  • For $\mathrm{\Gamma }=\pi$, it is a half-wave plate. It can rotate the plane of linearly polarised light or convert right-circularly polarised light into left-circularly polarised light, and vice versa.
• Ideal polarisation rotator that rotates the plane of linear polarisation by an angle $\theta$ counter-clockwise:$${\mathbf{T}}_{\text{rot}}(\theta )=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)$$

The Jones matrices for wave retarders given above assume their principal axes (fast/slow) are aligned with the $x$ and $y$ coordinate axes. If a wave retarder (whose fast axis is, say, along its own $x^{\prime }$-axis) is rotated by an angle $\theta$ with respect to the laboratory $x$-axis, its Jones matrix ${\mathbf{T}}^{\prime }$ in the lab frame is obtained by a similarity transformation:

where $\mathbf{R}(\theta )=\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right)$ is the coordinate rotation matrix from lab to retarder frame (and $\mathbf{R}(-\theta )$ is its inverse, from retarder to lab frame).
This transformation shows, for instance, that a half-wave plate with its fast axis at an angle $\theta$ to an incident linear polarisation will rotate that linear polarisation by an angle $2\theta$. Some more examples:

Generating arbitrary polarisation states
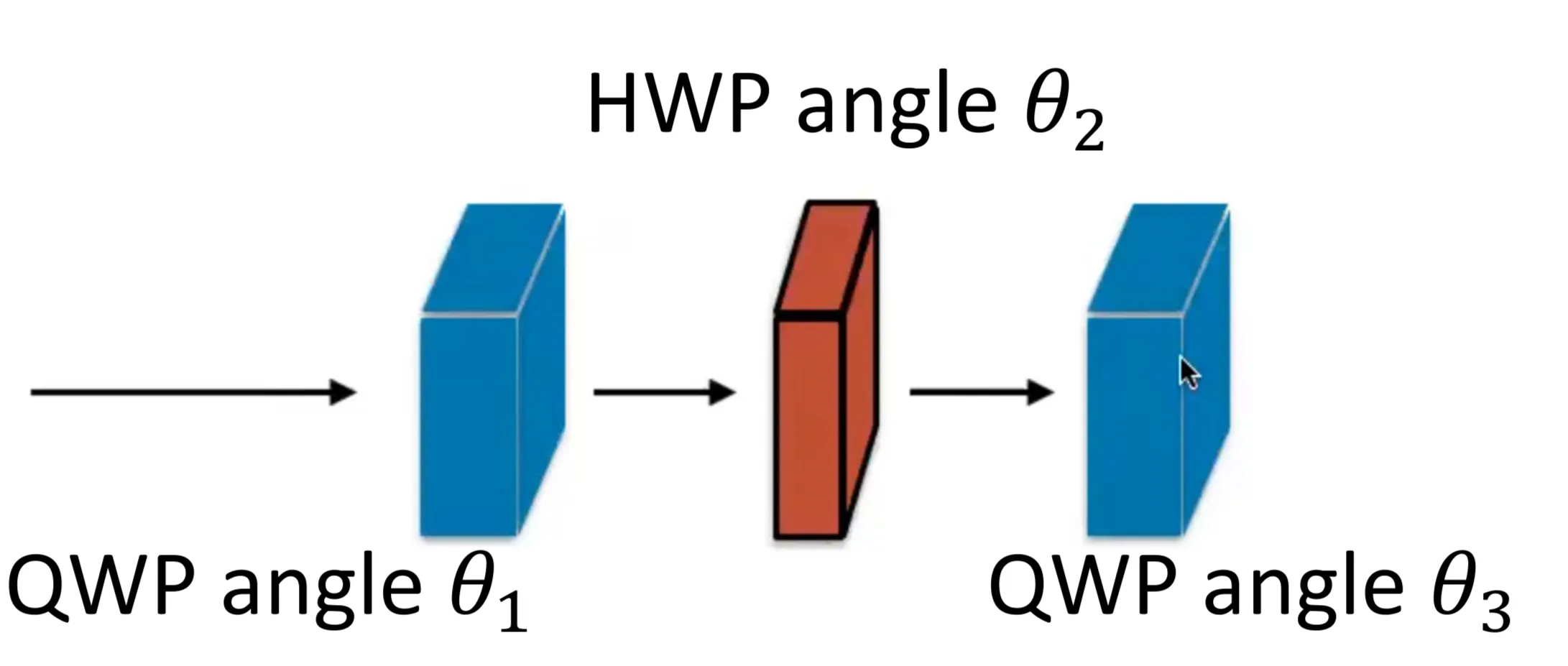
Using a sequence of wave plates, it is possible to transform any given input polarisation state into any desired output polarisation state. For instance, starting with linearly polarised light, an arbitrary polarisation state can be generated using a combination of a quarter-wave plate (QWP) and a half-wave plate (HWP), often followed by another QWP for full generality.
A common setup is QWP(${\theta }_1$) - HWP(${\theta }_2$) - QWP(${\theta }_3$), where ${\theta }_i$ are the orientation angles of the fast axes.

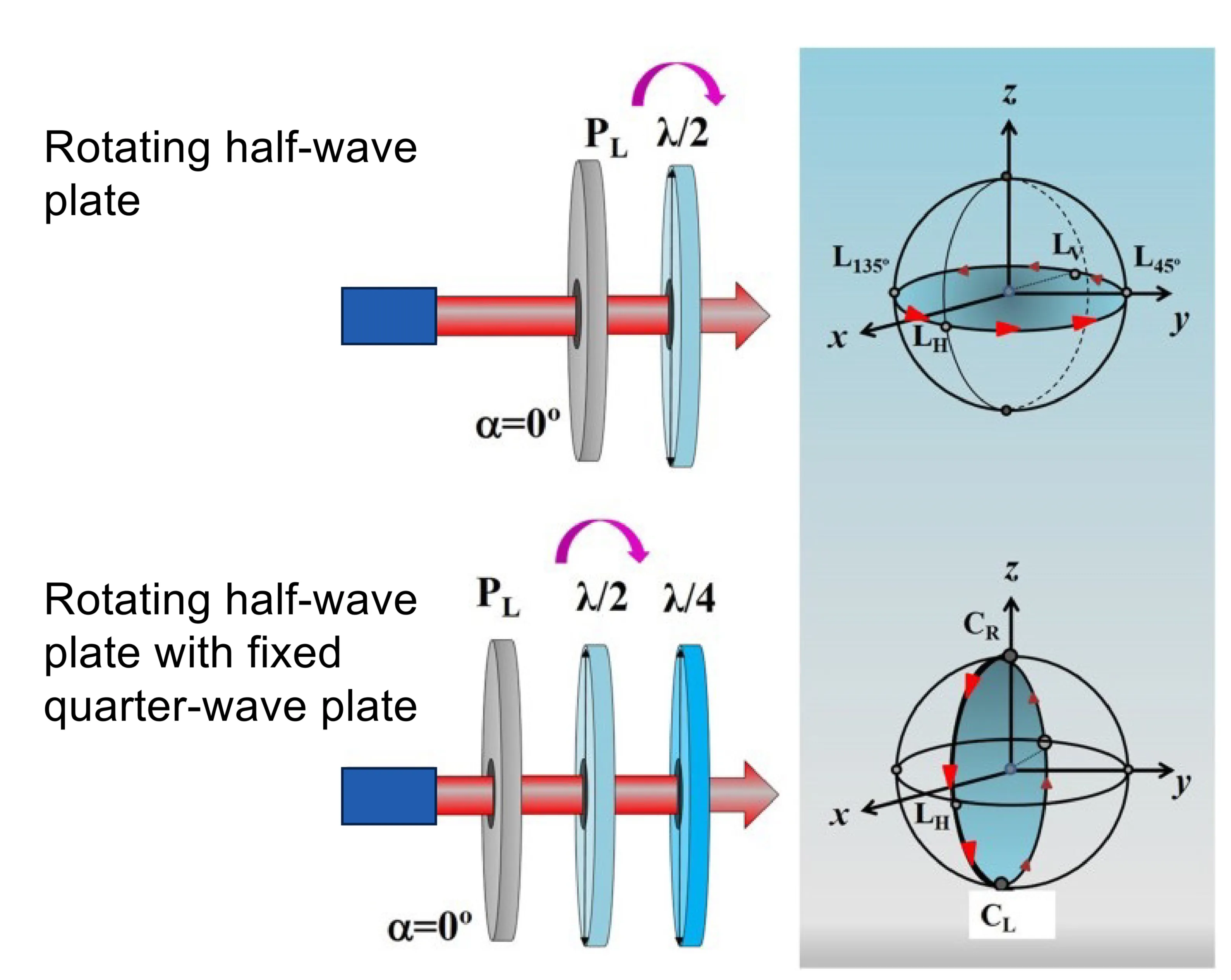
Figure illustrates how HWP rotates states on the equator, and QWP+HWP can move states off the equator.

The Jones matrix for an element (like a QWP or HWP, whose standard matrix is $\mathbf{J}(0)$ when aligned with axes) rotated by an angle $\theta$ is ${\mathbf{J}}_{\text{element}}(\theta )=\mathbf{R}(-\theta ){\mathbf{J}}_{\text{element}}(0)\mathbf{R}(\theta )$. The final Jones matrix of the system is a product of three such matrices:

Since each Jones matrix for an ideal (lossless) wave plate is unitary, their product is also unitary. A general $2\times 2$ unitary matrix with determinant 1 (an element of SU(2)) has three independent parameters, which can be mapped to the three rotation angles ${\theta }_1,{\theta }_2,{\theta }_3$.
The total Jones matrix transforms an arbitrary input polarisation ${\mathbf{E}}_{\text{in}}$ (represented as a Jones vector) as:

Since any SU(2) transformation corresponds to a rotation on the Poincaré sphere, this setup can convert any input polarisation state into any other output polarisation state. Essentially, the first QWP can transform an initial linear polarisation into a general elliptical state. The HWP can then rotate this elliptical state on the Poincaré sphere (effectively changing its orientation $\psi$ and ellipticity $\chi$ magnitude). The second QWP provides the final adjustment needed to reach any arbitrary point on the sphere.

9.3 Anisotropic Materials

Thinking back to the assumptions made in chapter 1, we will now relax one of them: the assumption of an isotropic material.

The isotropy assumption stated: $\mathbf{P}$ and $\mathbf{M}$ align with $\mathbf{E}$ and $\mathbf{B}$ (or $\mathbf{H}$), respectively, either in the same or opposite direction. This implies that the susceptibility, permittivity, and permeability are scalar quantities. This assumption is violated in many crystalline materials and other ordered media.

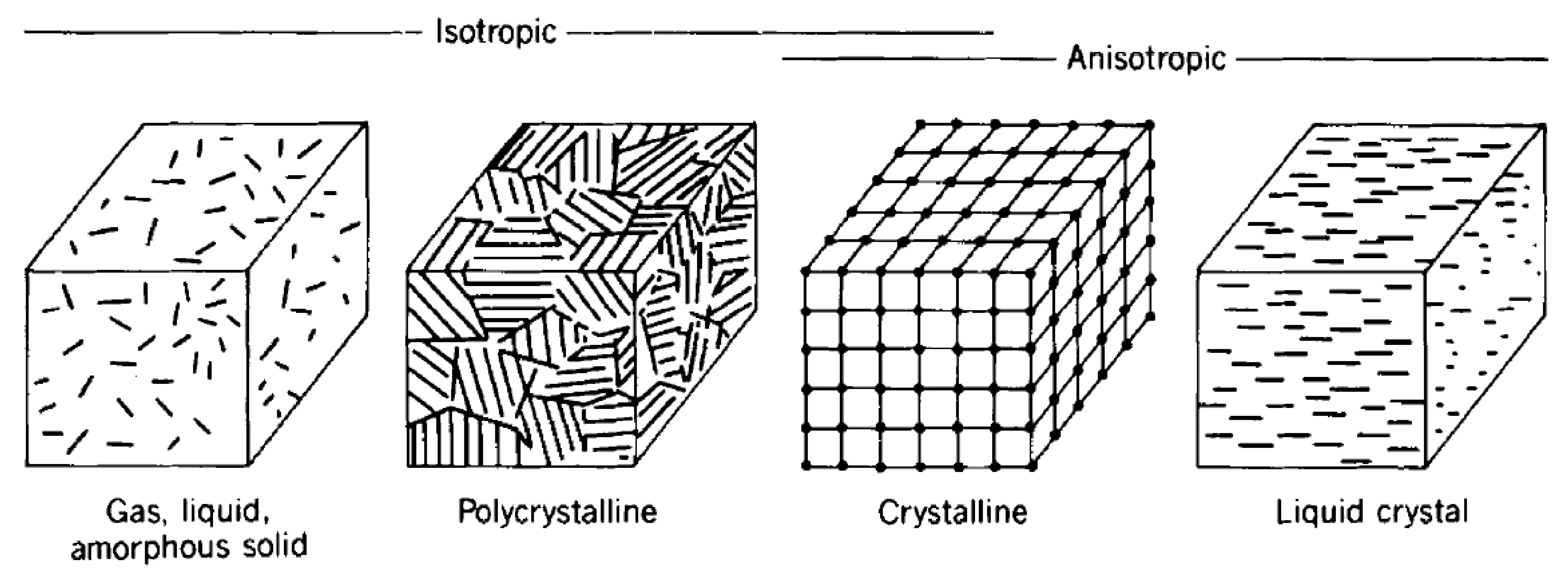
Many real materials are not isotropic. This is true for any material that exhibits some form of structural order over scales comparable to or larger than molecular dimensions, such as single crystals or liquid crystals. In such anisotropic materials, the optical properties (like refractive index) depend on both the direction of light propagation and its polarisation state. Examples of isotropic materials include amorphous solids (like glass), gases, most liquids, and polycrystalline materials if the crystallites are randomly oriented and much smaller than the wavelength.

On a macroscopic scale, isotropic media do not possess a directional dependence of their optical properties. Even cubic crystals, due to their high degree of symmetry, are optically isotropic.

We will now adjust our previously derived equations to account for anisotropic materials. The primary change is that the scalar electric susceptibility ${\chi }_e$ (and thus relative permittivity ${\epsilon }_r$) becomes a second-rank tensor ${\mathit{\chi }}_e$ (or ${\mathit{\epsilon }}_r$).
In an isotropic material, $\mathbf{D}$ is parallel to $\mathbf{E}$ ($\mathbf{D}={\epsilon }_0{\epsilon }_r\mathbf{E}$). In an anisotropic material (assuming linearity but no optical activity for now), this relationship becomes tensorial:

The relative permittivity (dielectric constant) becomes the dielectric tensor ${\mathit{\epsilon }}_r$:

Similarly, for non-magnetic or weakly magnetic materials at optical frequencies, we typically still assume ${\mu }_r\approx 1$ (so $\mathbf{M}\approx 0$ and $\mathbf{B}\approx {\mu }_0\mathbf{H}$). If magnetism were significant and anisotropic, the relative permeability ${\mu }_r$ would also be a tensor: $B_j={\mu }_0\sum _k({\mu }_r{)}_{jk}{H}_k$.

Symmetries in the material's crystal structure impose symmetries on these tensors, reducing the number of independent components (Neumann's Principle: material property tensors must possess at least the symmetry of the point group of the crystal). For non-absorbing, non-optically active media, the dielectric tensor ${\mathit{\epsilon }}_r$ is real and symmetric (${\epsilon }_{jk}={\epsilon }_{kj}$). A real symmetric tensor can always be diagonalised by a suitable rotation of the coordinate system to its principal axes.
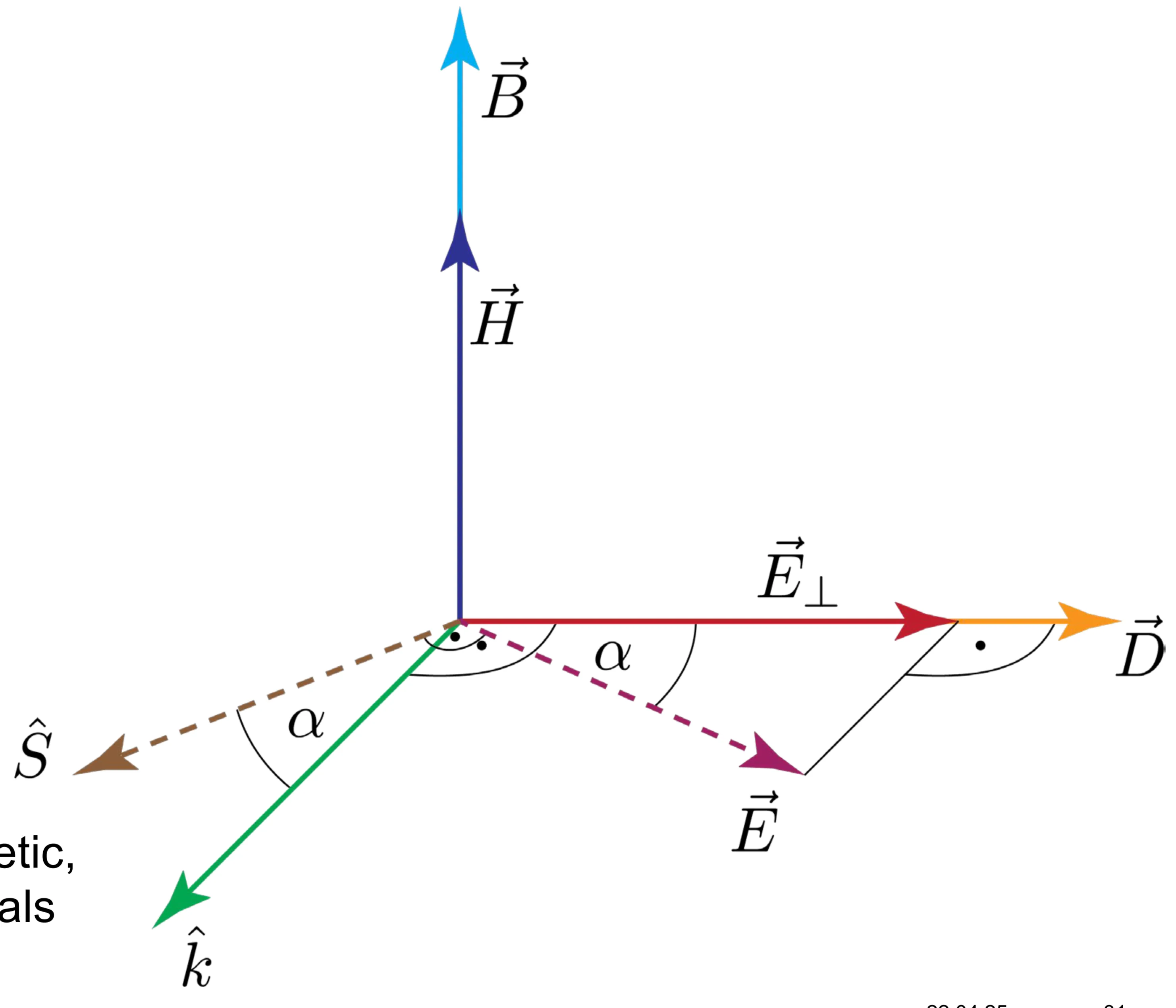
One way to visualise the dielectric tensor in the real, symmetric case is to consider the electric energy density $w_e$:

The equation $\sum _{j,k}({\epsilon }_r{)}_{jk}{E}_j{E}_k=\text{constant}$ defines an ellipsoid in $\mathbf{E}$-space. Alternatively, considering $\sum _{j,k}({\epsilon }_r^{-1}{)}_{jk}{D}_j{D}_k=\text{constant}$ defines the index ellipsoid (or optical indicatrix) in $\mathbf{D}$-space, which is more commonly used. In the principal axis system $(x^{\prime },y^{\prime },z^{\prime })$, the dielectric tensor is diagonal:

In this system, $D_{x^{\prime }}={\epsilon }_0{\epsilon }_{x^{\prime }}{E}_{x^{\prime }}$, $D_{y^{\prime }}={\epsilon }_0{\epsilon }_{y^{\prime }}{E}_{y^{\prime }}$, $D_{z^{\prime }}={\epsilon }_0{\epsilon }_{z^{\prime }}{E}_{z^{\prime }}$.
Note that even in the principal axis system, $\mathbf{D}$ and $\mathbf{E}$ are generally not parallel unless the field is aligned along one of the principal axes or unless ${\epsilon }_{x^{\prime }}={\epsilon }_{y^{\prime }}={\epsilon }_{z^{\prime }}$ (isotropic case).
The quantities $n_{x^{\prime }}=\sqrt{{\epsilon }_{x^{\prime }}}$, $n_{y^{\prime }}=\sqrt{{\epsilon }_{y^{\prime }}}$, $n_{z^{\prime }}=\sqrt{{\epsilon }_{z^{\prime }}}$ are the principal refractive indices.

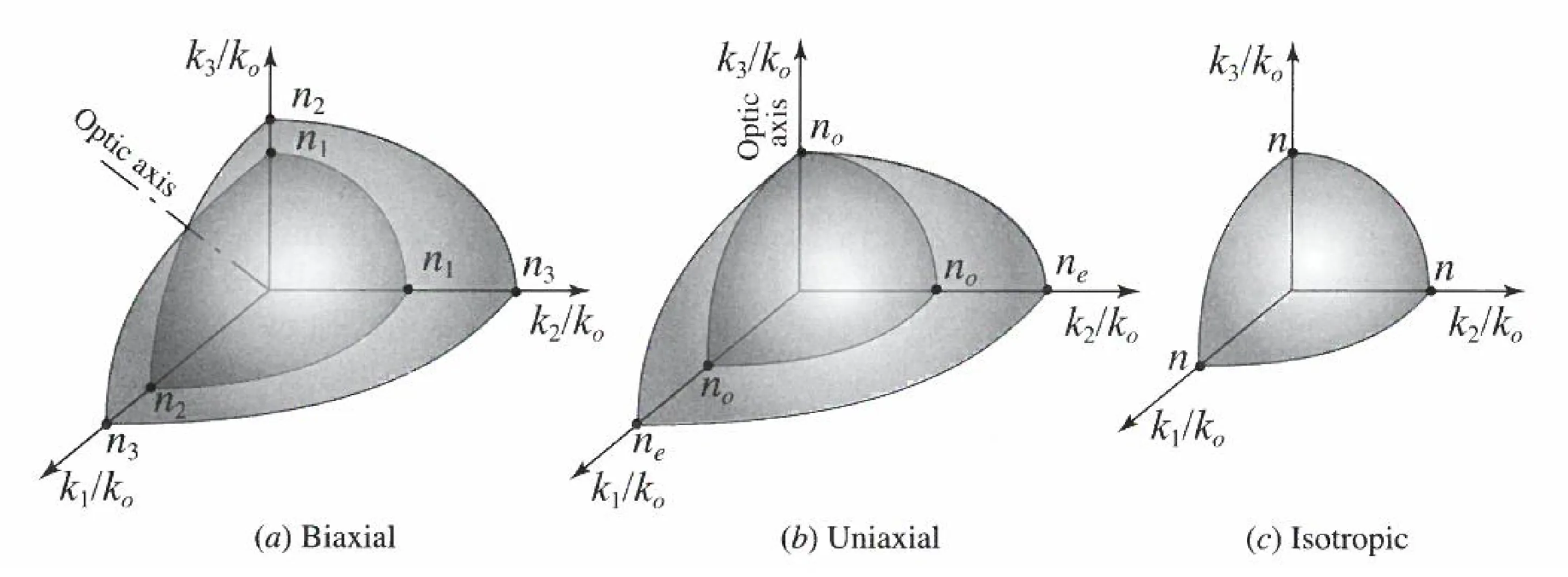
• Isotropic: $n_{x^{\prime }}=n_{y^{\prime }}=n_{z^{\prime }}$.
• Uniaxial: Two principal indices are equal (e.g., $n_{x^{\prime }}=n_{y^{\prime }}=n_o\ne n_{z^{\prime }}=n_e$). The $z^{\prime }$-axis is then the optic axis.
• Biaxial: All three principal indices are different.

For plane waves in non-magnetic, anisotropic media, the vectors $(\mathbf{D},\mathbf{H},\mathbf{k})$ form an orthogonal triad, and $(\mathbf{E},\mathbf{H},\mathbf{S})$ form another orthogonal triad. Crucially, $\mathbf{E}$ is not generally parallel to $\mathbf{D}$, and the Poynting vector $\mathbf{S}$ (direction of energy flow) is not generally parallel to the wavevector $\mathbf{k}$ (direction of phase propagation). The angle $\alpha$ between $\mathbf{S}$ and $\mathbf{k}$ is the walk-off angle.

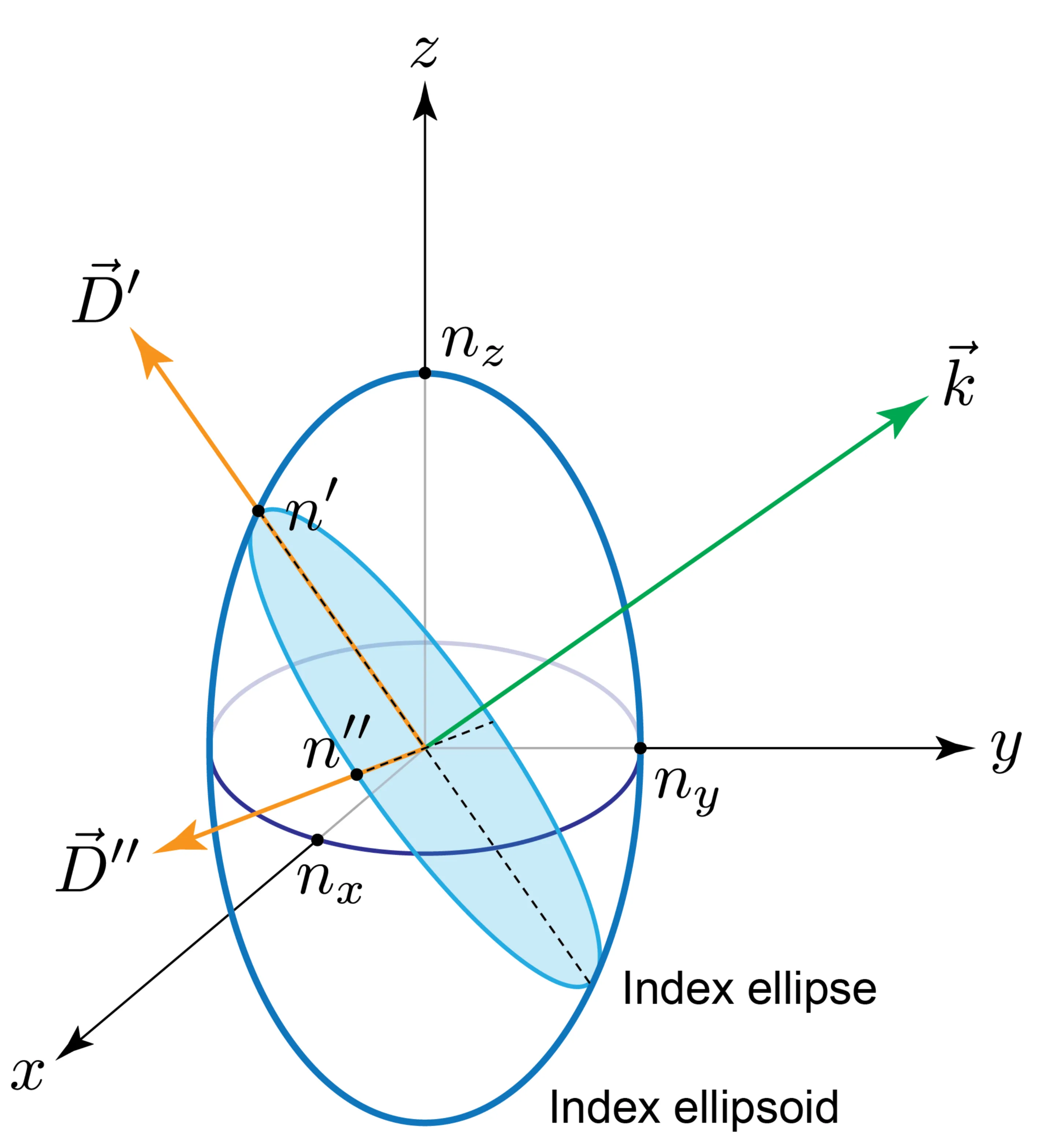
9.3.1 Index Ellipsoid and Ellipse

In the principal coordinate system $(x,y,z)$, the index ellipsoid (optical indicatrix) is defined by the equation:

where $n_x,n_y,n_z$ are the principal refractive indices.

For a given direction of wave propagation $\mathbf{k}$, the allowed polarisations (directions of $\mathbf{D}$) and corresponding refractive indices can be found by considering the intersection of a plane normal to $\mathbf{k}$ (passing through the origin) with the index ellipsoid. This intersection is an ellipse (the "index ellipse"). The semi-axes of this index ellipse give the two allowed refractive indices for waves propagating along $\mathbf{k}$, and their directions correspond to the two allowed orthogonal directions of $\mathbf{D}$ for these eigenpolarisations (normal modes). These two waves propagate with different phase velocities $c/n_1^{\prime }$ and $c/n_2^{\prime }$, where $n_1^{\prime }$ and $n_2^{\prime }$ are the lengths of the semi-axes.

If light is linearly polarised along one of the principal axes (say, $\mathbf{E}$ along $x$) and propagates along another principal axis (say, $z$), then $\mathbf{D}$ is parallel to $\mathbf{E}$, and the wave behaves as in an isotropic medium with refractive index $n_x$, propagating with phase velocity $c/n_x$.
If incident light propagates along a principal axis (say, $z$) but its polarisation is not aligned with another principal axis ($x$ or $y$), it can be decomposed into components along $x$ and $y$. These components travel with phase velocities $c/n_x$ and $c/n_y$, respectively. After propagating a distance $d$, the Jones vector changes from $\left(\begin{array}{c}{A}_x{e}^{i{\varphi }_x}\\ A_y{e}^{i{\varphi }_y}\end{array}\right)$ to $\left(\begin{array}{c}{A}_x{e}^{i({\varphi }_x-k_{x}d)}\\ A_y{e}^{i({\varphi }_y-k_{y}d)}\end{array}\right)$, where $k_x=n_x\omega /c$ and $k_y=n_y\omega /c$. The phase retardation $\mathrm{\Gamma }$ introduced between the two components is:

This is the principle of wave plates.

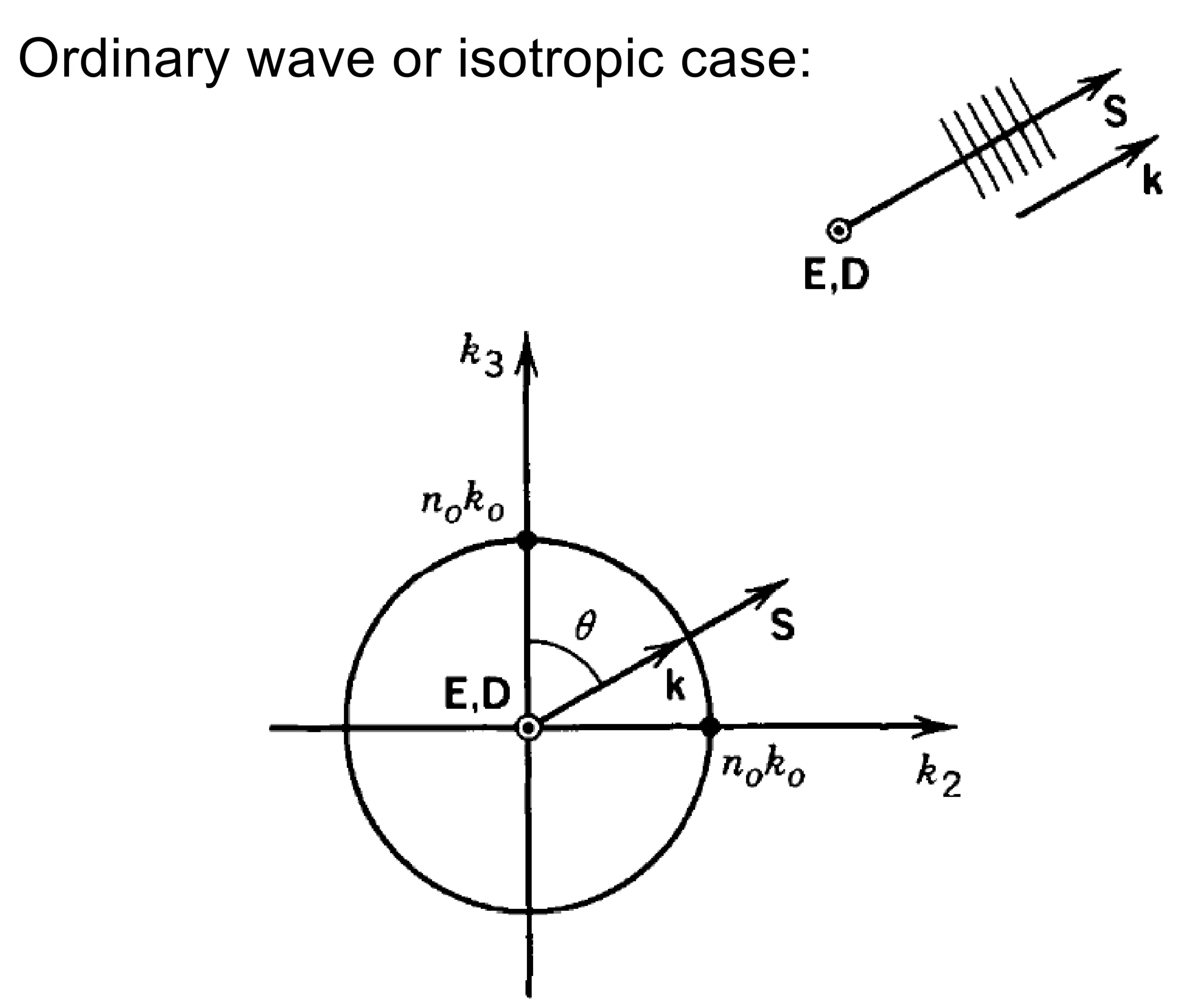
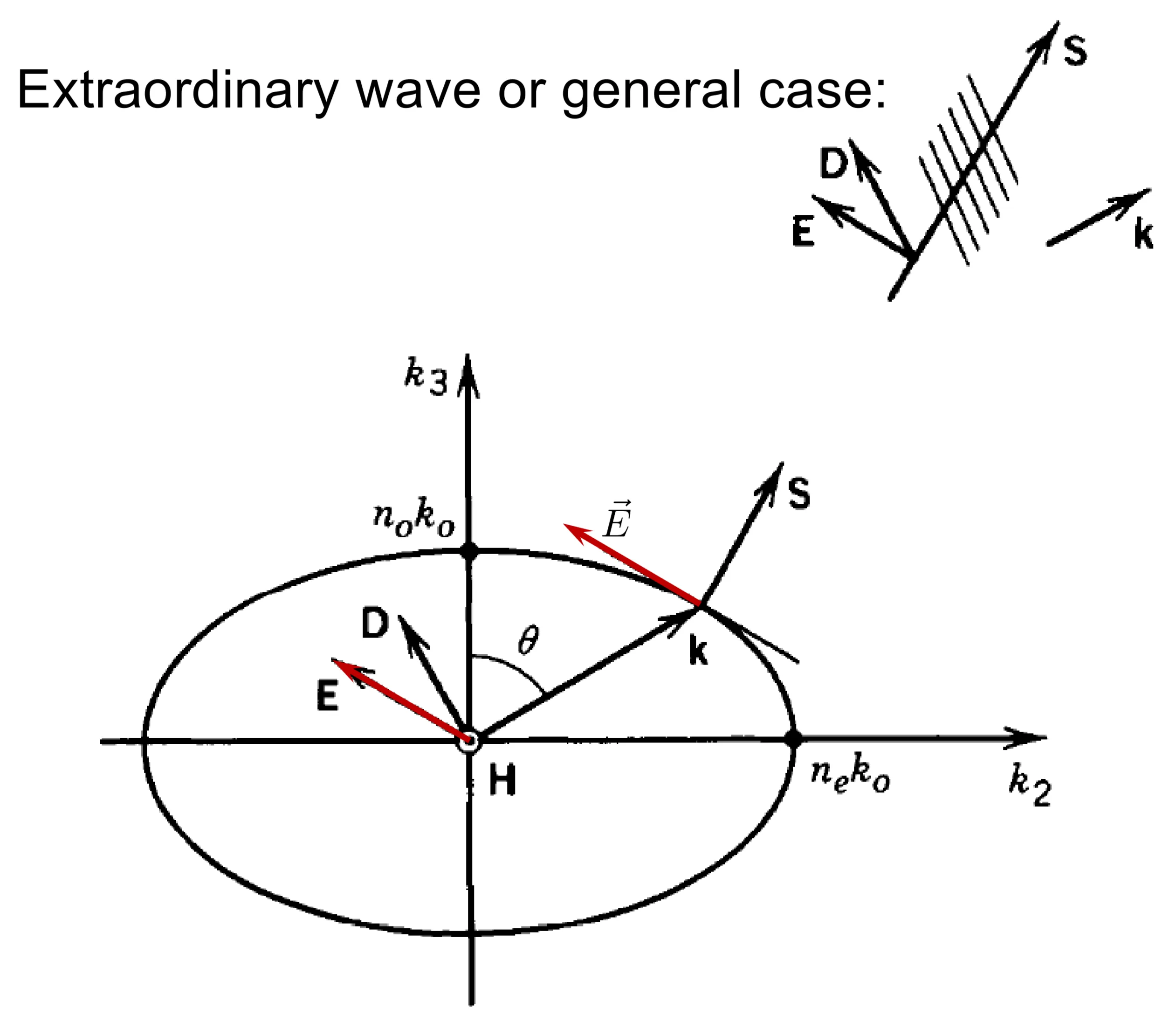
In a uniaxial crystal (with optic axis along $z$, so $n_x=n_y=n_o$ (ordinary index) and $n_z=n_e$ (extraordinary index)), if $\mathbf{k}$ makes an angle $\theta$ with the optic axis (z-axis):

• One normal mode is the ordinary wave (o-wave), polarised with its $\mathbf{D}$ vector (and $\mathbf{E}$) perpendicular to the plane containing $\mathbf{k}$ and the optic axis. It always experiences refractive index $n_o$. $\mathbf{S}$ is parallel to $\mathbf{k}$.
• The other normal mode is the extraordinary wave (e-wave), polarised with its $\mathbf{D}$ vector in the plane containing $\mathbf{k}$ and the optic axis (and $\mathbf{D}\perp \mathbf{k}$). Its refractive index $n_e(\theta )$ depends on $\theta$:$$\frac{1}{n_e(\theta {)}^2}=\frac{{\cos }^2\theta }{n_o^2}+\frac{{\sin }^2\theta }{n_e^2}.$$

For the e-wave, $\mathbf{E}$ is not generally parallel to $\mathbf{D}$, and $\mathbf{S}$ is not generally parallel to $\mathbf{k}$ (walk-off occurs).

9.3.2 Dispersion Relation

The dispersion relation $\omega (\mathbf{k})$ in an anisotropic medium is more complex than $\omega =c|\mathbf{k}|/n$. The relation $\mathbf{k}\times (\mathbf{k}\times \mathbf{E})+{\omega }^2{\mu }_0\mathbf{D}=0$ leads to a matrix equation for the components of $\mathbf{E}$ (or $\mathbf{D}$) in the principal axis system:

where $k_0=\omega /c$. For non-trivial solutions, the determinant of this matrix must be zero. This condition defines a 3D surface in k-space for a given $\omega$, known as the normal surface or k-surface. It generally consists of two sheets, corresponding to the two allowed eigenpolarisations.

For a uniaxial crystal with optic axis along $z$ ($n_x=n_y=n_o,n_z=n_e$), the determinant condition simplifies to:

This yields two solutions for $|\mathbf{k}{|}^2=k_x^2+k_y^2+k_z^2$:

1. A sphere: $k_x^2+k_y^2+k_z^2=n_o^2{k}_0^2$ (ordinary wave).
2. An ellipsoid of revolution: $\frac{k_x^2+k_y^2}{n_e^2}+\frac{k_z^2}{n_o^2}=k_0^2$ (extraordinary wave).

In a 2D plot (assuming $k_y=0$ without loss of generality due to rotational symmetry around optic axis):

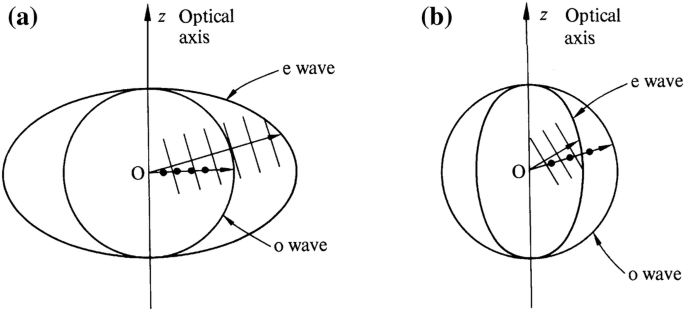
The effective refractive index for the extraordinary wave whose wavevector $\mathbf{k}$ makes an angle $\theta$ with the optic axis (z-axis) is $n_e(\theta )$, given by $\frac{1}{n_e(\theta {)}^2}=\frac{{\sin }^2\theta }{n_e^2}+\frac{{\cos }^2\theta }{n_o^2}$.

The directions of $\mathbf{E}$, $\mathbf{D}$, $\mathbf{S}$, and $\mathbf{k}$ for ordinary and extraordinary waves are shown:

For the o-wave, $\mathbf{S}\parallel \mathbf{k}$. For the e-wave, $\mathbf{S}$ is generally not parallel to $\mathbf{k}$ (walk-off). $\mathbf{E}$ is tangential to the normal surface at point $\mathbf{k}/k_0$.

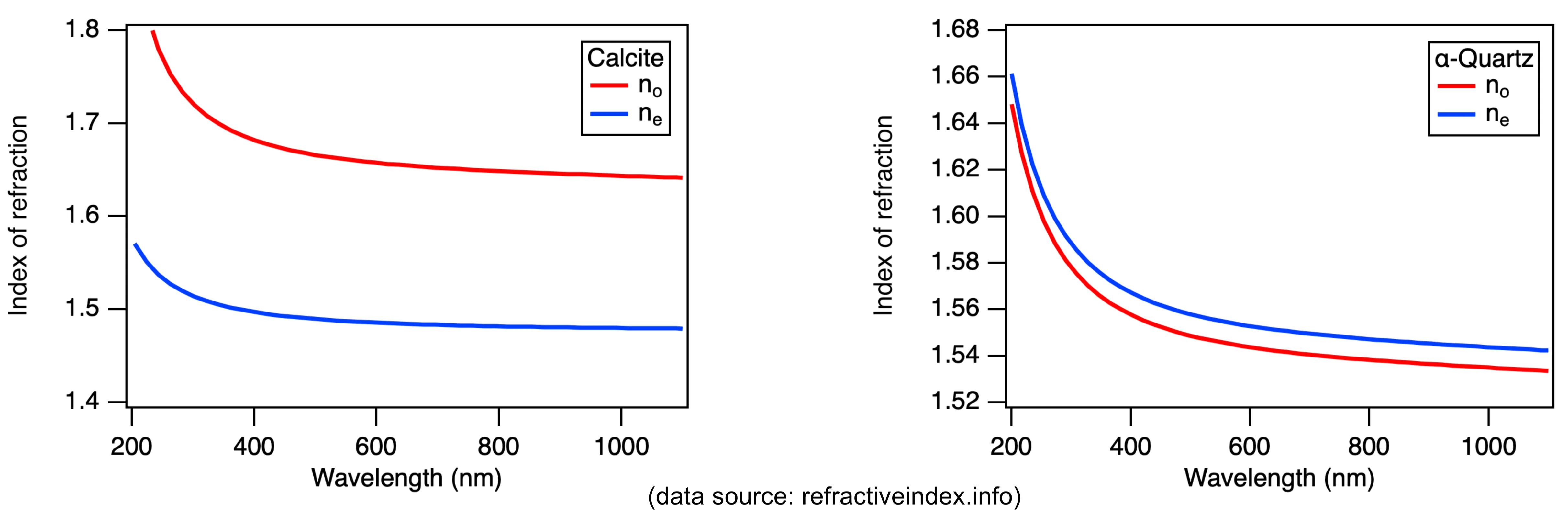
Examples of uniaxial crystals are calcite ($n_e<n_o$, negative uniaxial) and quartz ($n_e>n_o$, positive uniaxial).

9.3.3 Refraction at Interfaces

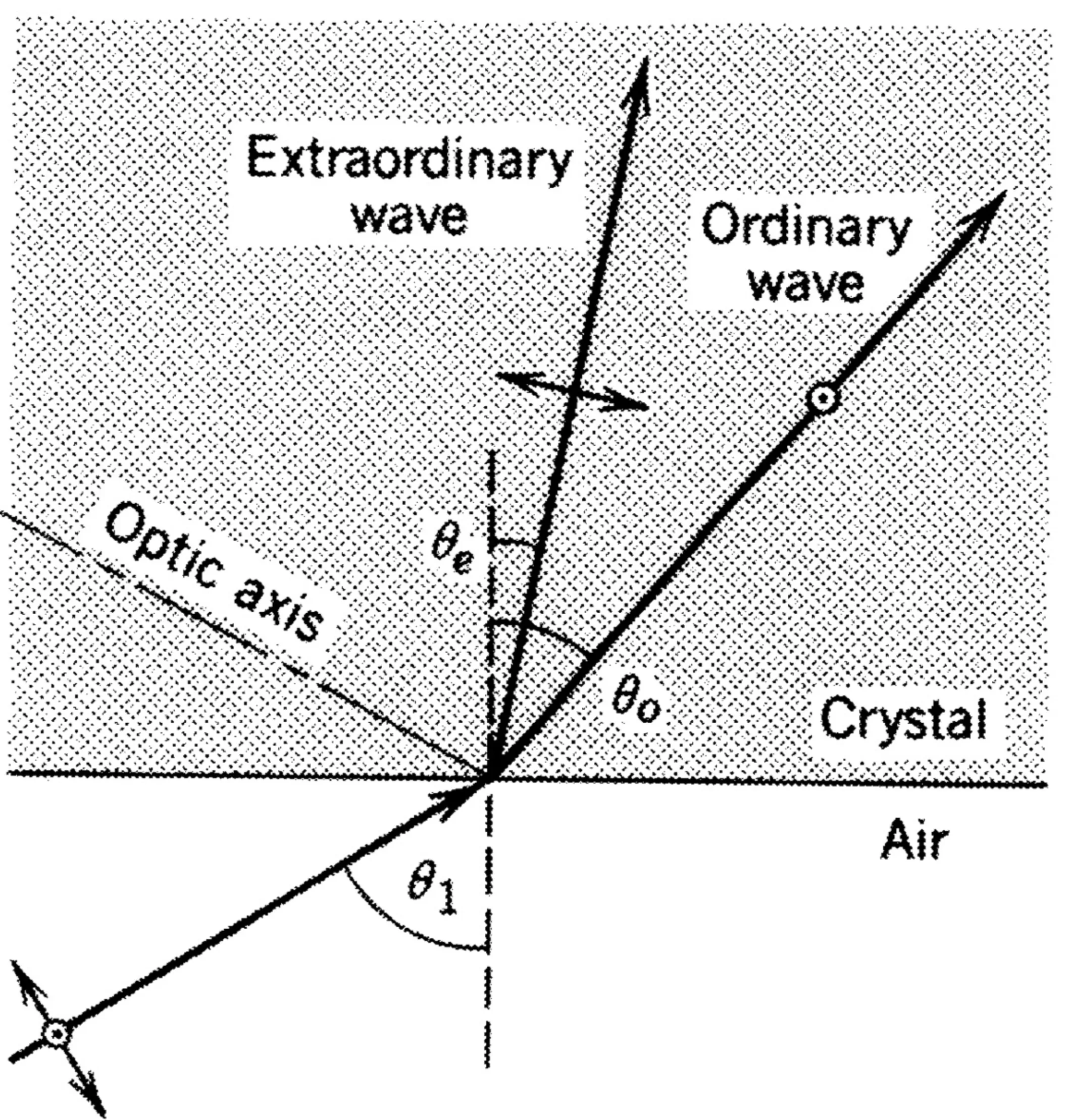
Birefringence (double refraction) occurs when an unpolarised or generally polarised light beam is incident obliquely on the surface of an anisotropic crystal. The incident wave generally splits into two refracted waves (o-wave and e-wave) that travel in different directions with different polarisations and speeds.

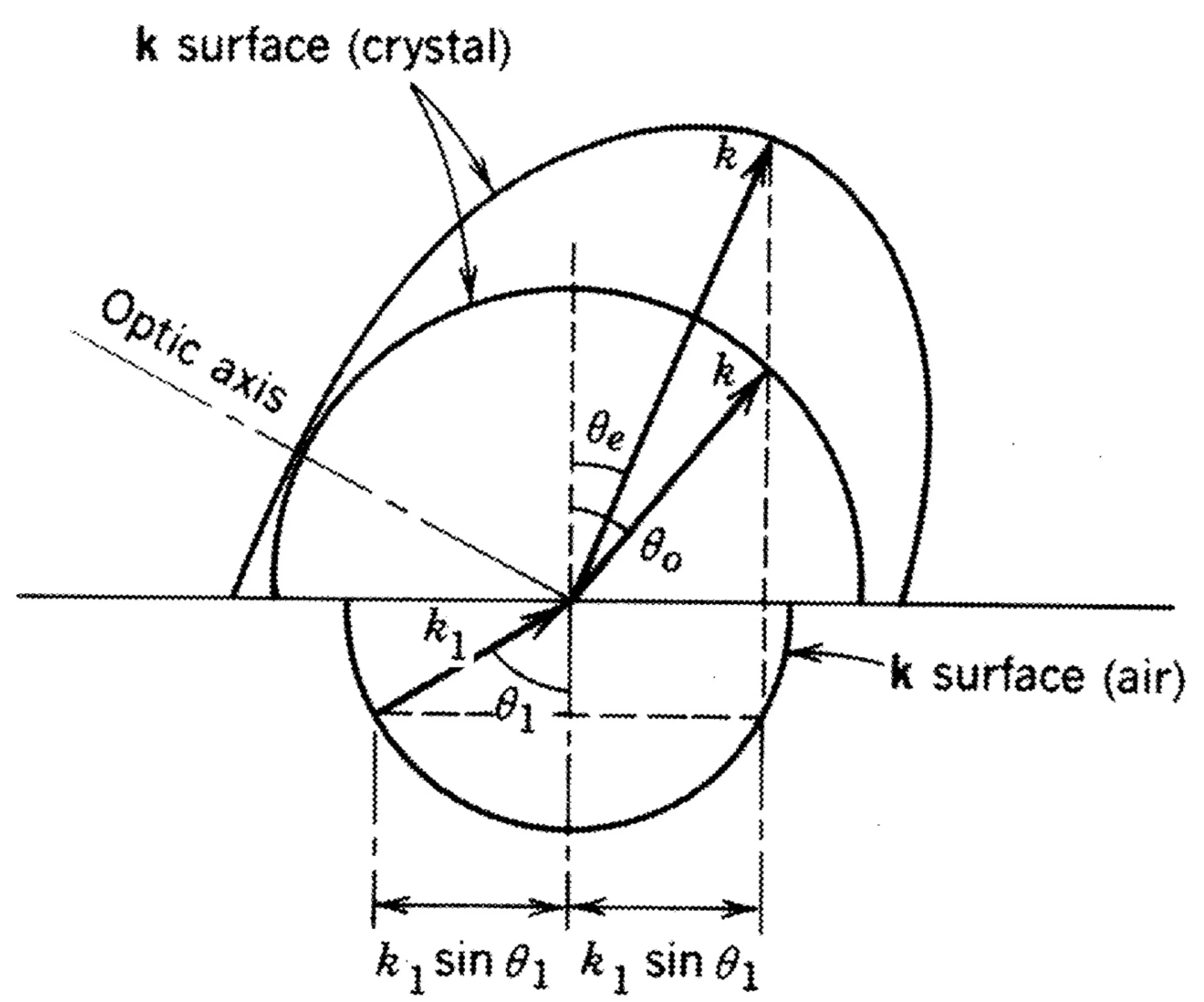
The directions of the refracted waves are determined by applying the boundary condition that the tangential component of $\mathbf{k}$ must be conserved across the interface, separately for the o-wave and e-wave using their respective k-surfaces.

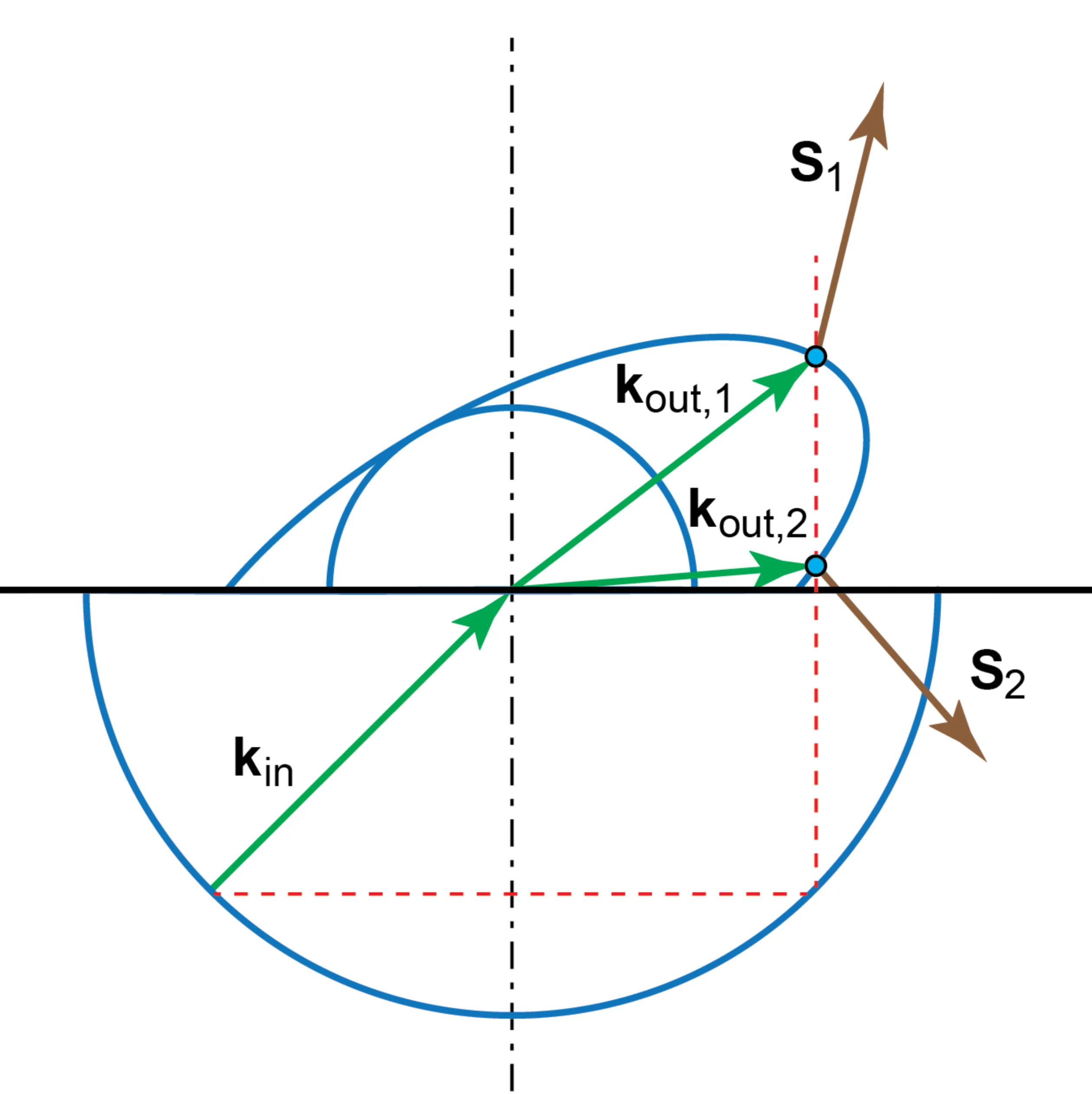
Figure showing that for a given incident $k_{\parallel }$, two $k$-vectors might satisfy the e-wave normal surface condition, but only one has energy flow (Poynting vector $\mathbf{S}$) directed into the second medium.

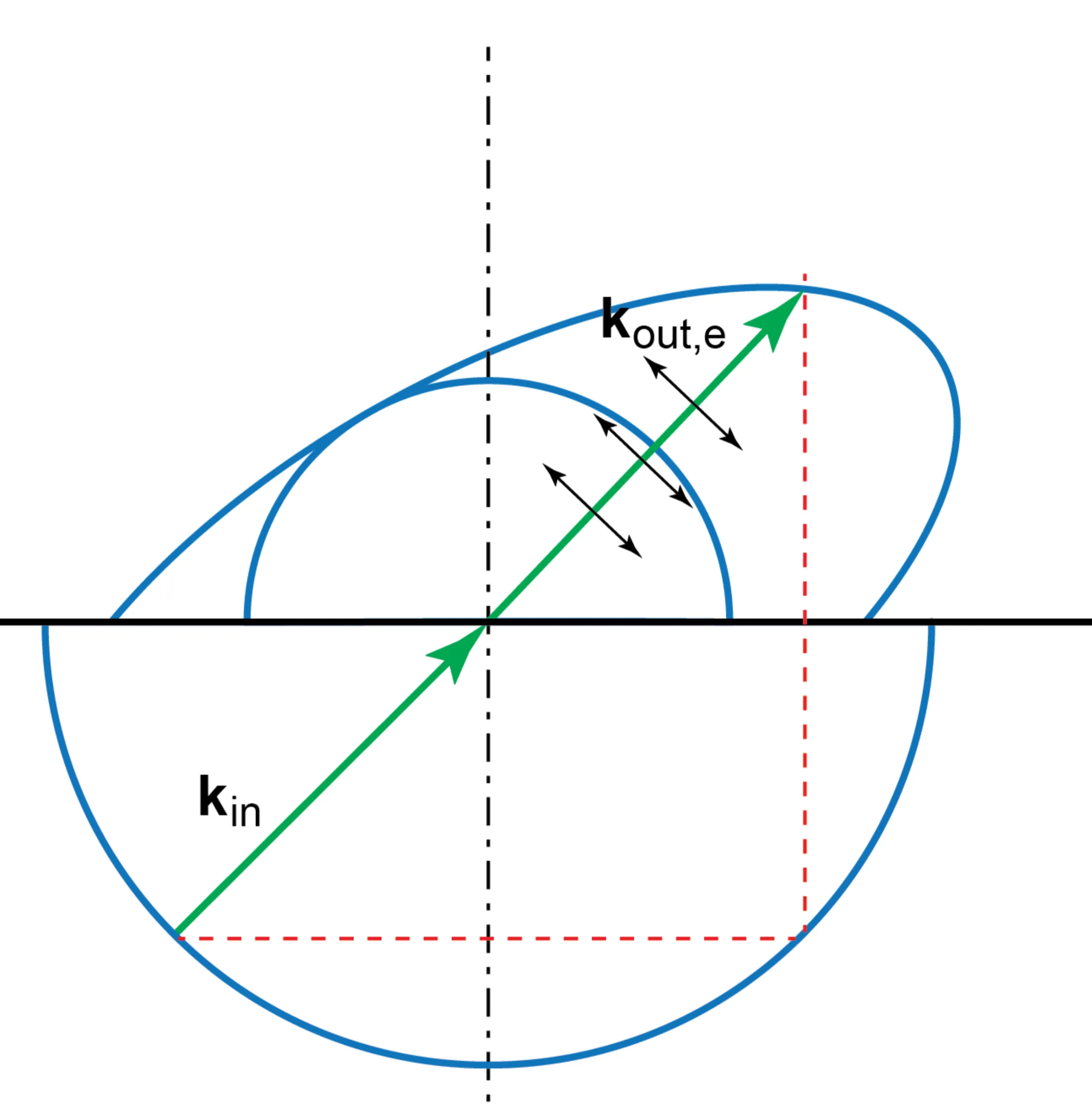
Figure showing a scenario where s-polarised light might undergo TIR while p-polarised light (as an e-wave) is refracted, or vice-versa, used in polarisers.

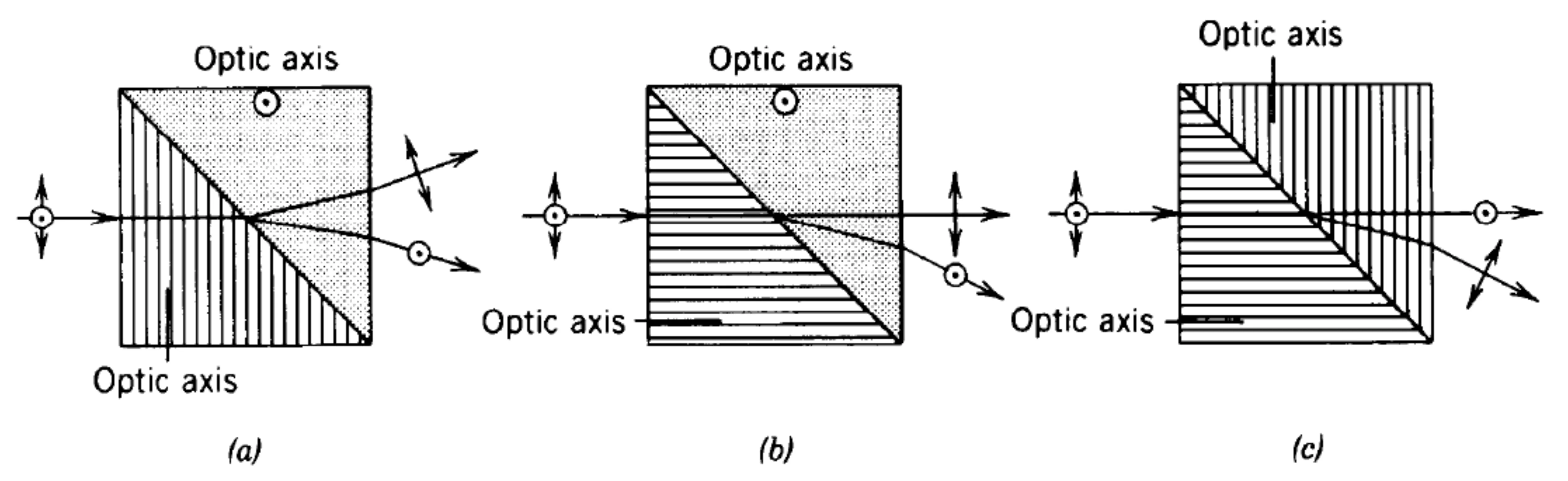
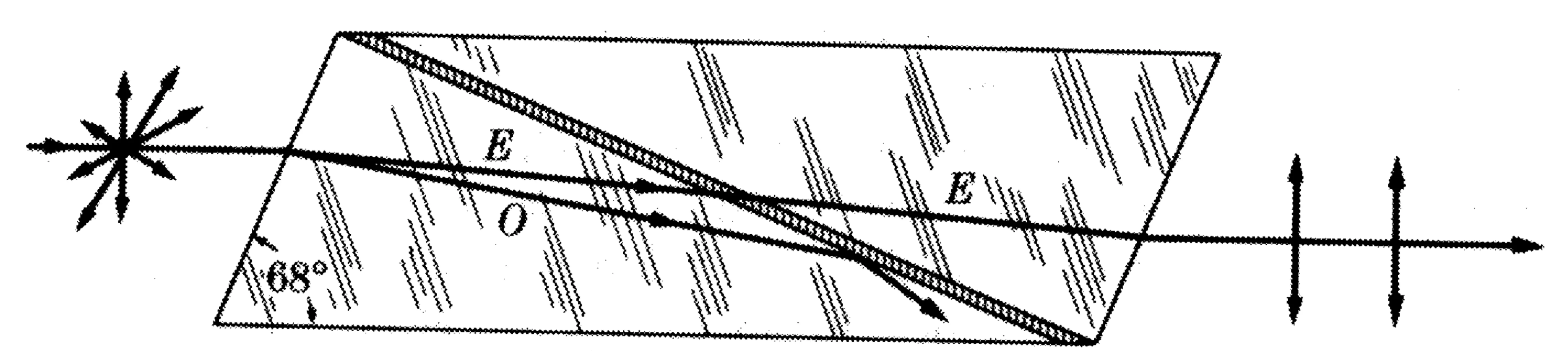
This effect is used in polarising beamsplitters like the Wollaston, Rochon, and Sénarmont prisms, which use birefringent crystals to spatially separate the two orthogonal polarisation components.

The Nicol prism is another classic polariser based on birefringence and TIR in calcite.

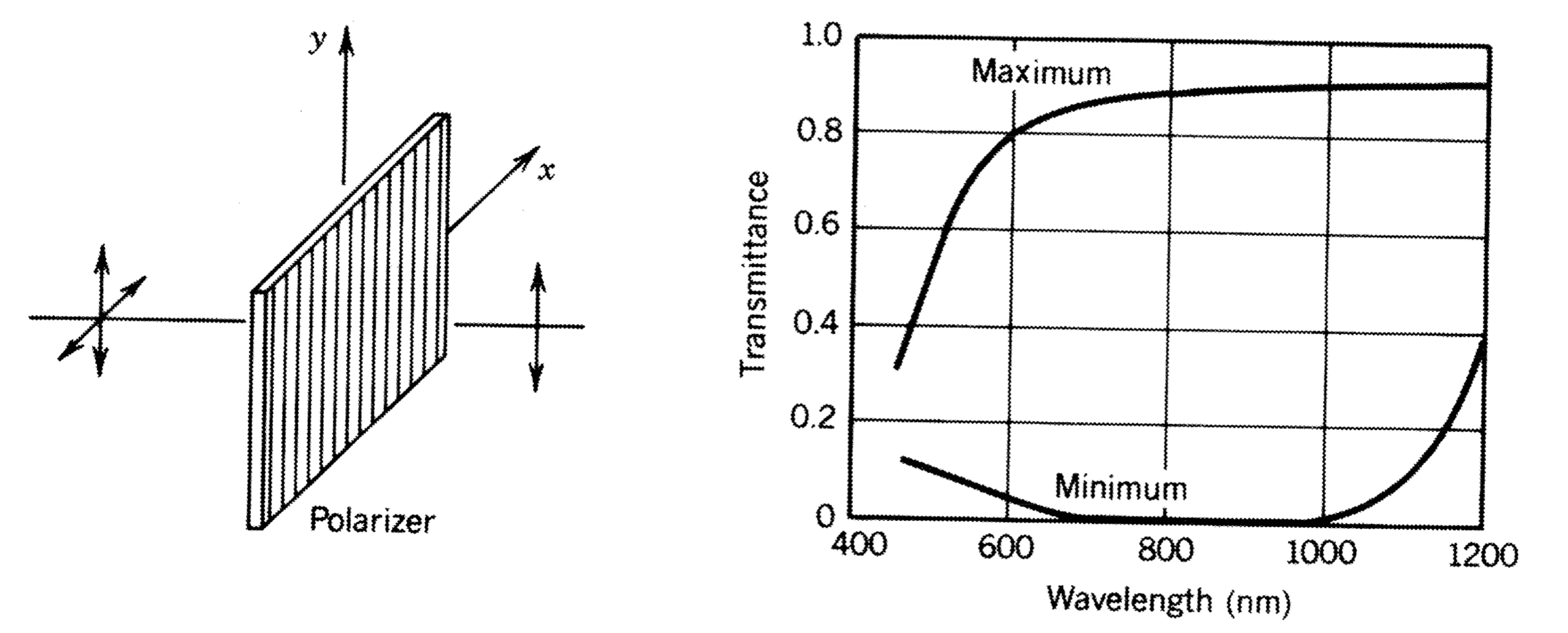
9.3.4 Dichroism

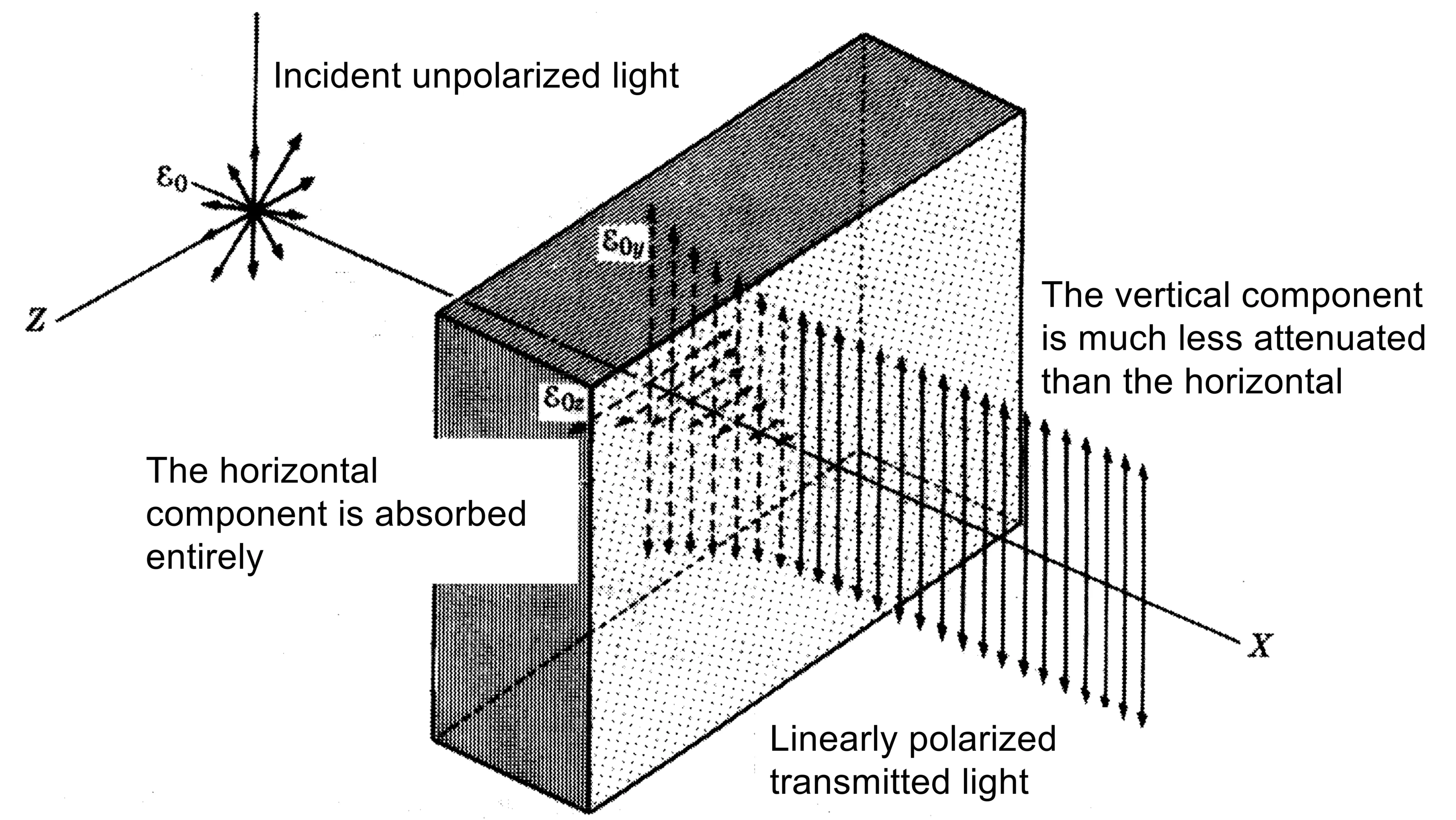
Dichroism is the property of some anisotropic materials to exhibit polarisation-dependent absorption. One polarisation component is absorbed much more strongly than the orthogonal component.

This is used in dichroic sheet polarisers (like Polaroid film), which consist of aligned absorbing molecules or crystals that preferentially absorb light polarised along one direction.

9.4 Optical Activity

Optical activity is the property of certain materials to rotate the plane of polarisation of linearly polarised light as it propagates through them. This occurs in materials that are chiral (lacking mirror symmetry in their molecular or crystal structure), such as quartz, sugar solutions, and some organic molecules.
In these materials, the dielectric tensor ${\mathit{\epsilon }}_r$ is not symmetric (${\epsilon }_{jk}\ne {\epsilon }_{kj}$); it possesses an antisymmetric part, or more generally, the material equations include terms coupling $\mathbf{E}$ to $\mathrm{\nabla }\times \mathbf{E}$ (spatial dispersion of a particular kind). The normal modes of propagation in an optically active material are right-circularly polarised (RCP) and left-circularly polarised (LCP) light, which travel with different phase velocities (i.e., experience different refractive indices $n_{+}$ and $n_{-}$).

Consider linearly polarised light incident on such a medium. It can be decomposed into a sum of RCP and LCP components of equal amplitude:
A Jones vector for x-polarised light is ${\mathbf{J}}_{\text{in}}=\left(\begin{array}{c}1\\ 0\end{array}\right)=\frac{1}{2}[{\left(\begin{array}{c}1\\ -i\end{array}\right)}_{\text{LCP}}+{\left(\begin{array}{c}1\\ i\end{array}\right)}_{\text{RCP}}].$
After propagating a distance $d$ through an optically active material with refractive indices $n_{+}$ for RCP and $n_{-}$ for LCP light, the output Jones vector (ignoring a common phase factor) is:

This simplifies to (up to an overall phase):

This is still linearly polarised light, but its plane of polarisation has been rotated by an angle $\mathrm{\Delta }\theta =\frac{\pi d}{{\lambda }_0}(n_{-}-n_{+})$. The direction of rotation depends on which circular component travels faster.

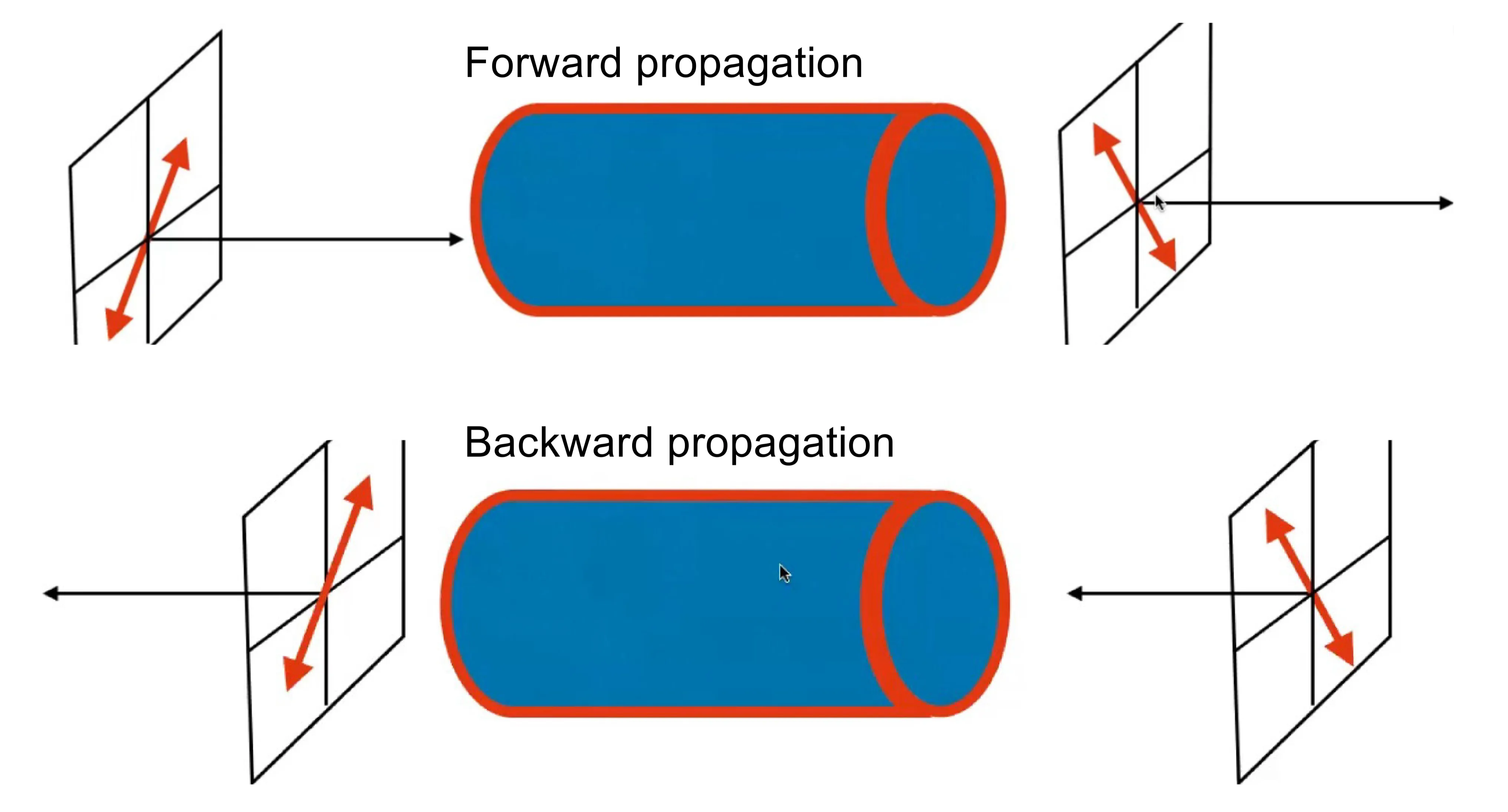
Optical activity is a reciprocal effect: if light passes through the medium, is reflected by a mirror, and passes back through the medium, the rotation induced on the return trip cancels the initial rotation. The polarisation returns to its original state.

9.5 Magneto-Optics

Magneto-optics deals with phenomena where the optical properties of a medium are altered by the presence of a quasi-static external magnetic field. This modification of optical properties is a form of nonlinear optics, though often treated within a linear response framework for the light fields once the magnetic field's influence on material parameters is established. A more in-depth discussion can be found in the crystal optics course.

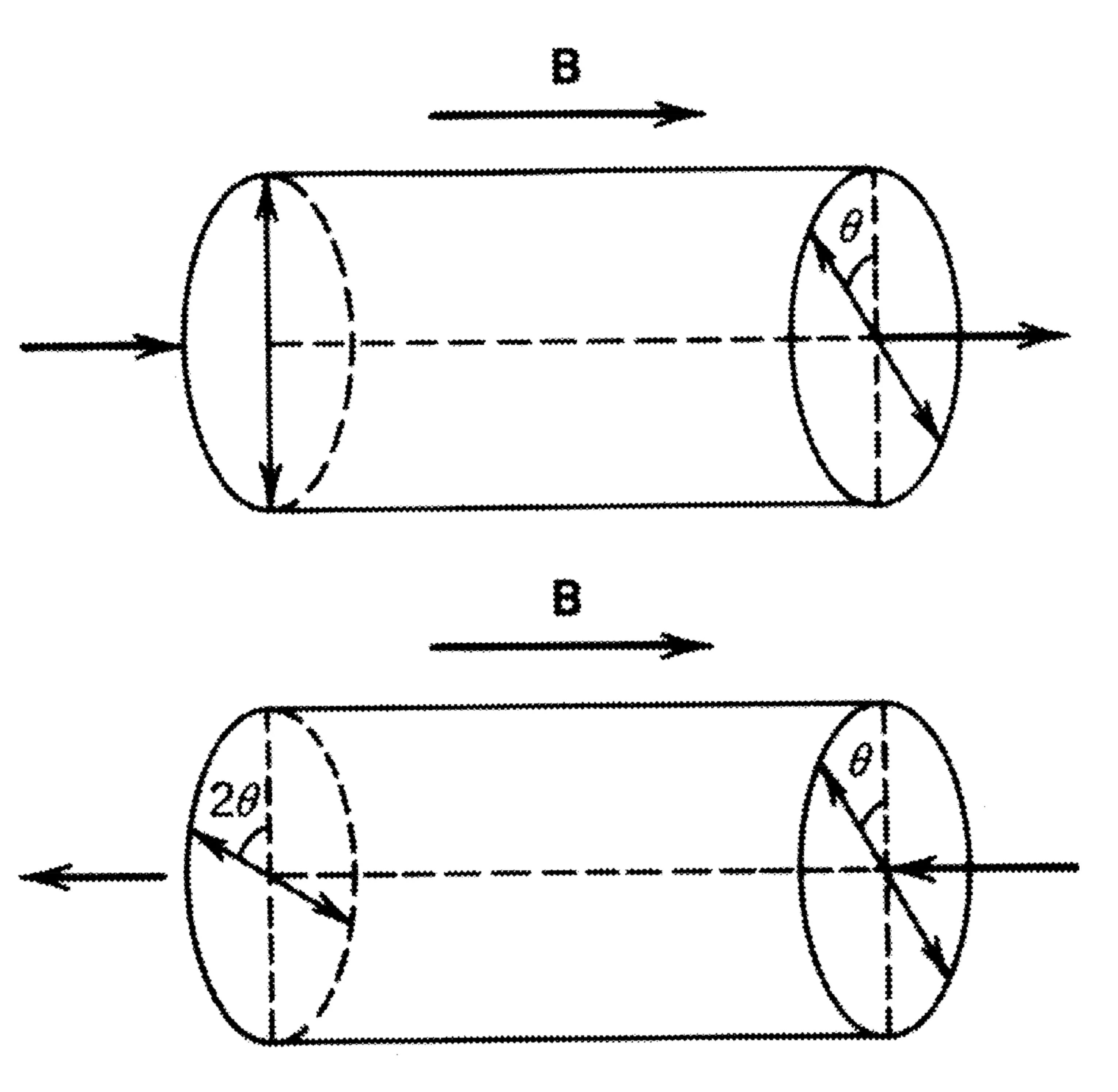
One prominent magneto-optic effect is the Faraday effect: when linearly polarised light propagates through certain materials subjected to a static magnetic field parallel to the light's propagation direction, the plane of polarisation rotates. The angle of rotation $\mathrm{\Delta }{\theta }_F$ is proportional to the magnetic field strength component $B_z$ along the propagation direction and the path length $d$:

where $\mathcal{V}$ is the Verdet constant, a material- and wavelength-dependent parameter. Typical values for $\mathcal{V}$ are around $3\times {10}^{-4}\text{degrees}/(\text{Gauss}\cdot \text{cm})$ (or $\sim 0.03\text{rad}/(\text{T}\cdot \text{m})$) at optical wavelengths for glasses.
A key difference between the Faraday effect and natural optical activity is that the Faraday effect is non-reciprocal; it breaks time-reversal symmetry due to the axial nature of the magnetic field (which is a c-type tensor, odd under time reversal).

If linearly polarised light passes through a Faraday rotator, its polarisation rotates by $\mathrm{\Delta }{\theta }_F$. If it is then reflected and passes back through the rotator in the opposite direction, the magnetic field direction relative to the light's new propagation direction is unchanged (if $\mathbf{B}$ is fixed in space). Consequently, the rotation adds further, resulting in a total rotation of $2\mathrm{\Delta }{\theta }_F$ relative to the input polarisation upon exiting. This non-reciprocal property is utilised in optical isolators (Faraday isolators), which allow light to pass in one direction but block or attenuate it in the reverse direction.

9.6 Electro-Optics

Electro-optics concerns the modification of a material's optical properties by an applied quasi-static or low-frequency external electric field ${\mathbf{E}}^{(0)}$.

• The Pockels effect (or linear electro-optic effect) describes a change in the refractive index (or, more generally, the impermeability tensor) that is linearly proportional to the applied electric field. It occurs only in non-centrosymmetric crystals.
• The Kerr effect (or quadratic electro-optic effect) describes a change in the refractive index proportional to the square of the applied electric field. It can occur in all materials (gases, liquids, solids, including centrosymmetric ones).

Mathematically, these effects are described by changes to the impermeability tensor $\mathit{\eta }={\mathit{\epsilon }}_r^{-1}$ (where ${\mathit{\epsilon }}_r$ is the relative permittivity tensor):

Here:

• ${\eta }_{jk}(0)$ is the impermeability tensor element in the absence of the external field ${\mathbf{E}}^{(0)}$.
• $r_{jkl}$ is the linear electro-optic (Pockels) coefficient (a third-rank tensor).
• $s_{jklm}$ is the quadratic electro-optic (Kerr) coefficient (a fourth-rank tensor).
  The specific non-zero elements of these tensors are determined by the crystal symmetry of the material, as per Neumann's principle.
  These effects are widely used to create devices that rapidly control the phase, polarisation, or intensity of light, such as Pockels cells (used as fast optical switches or modulators) and Kerr cells.