Jump back to chapter selection.

Table of Contents

10.1 Planar Mirror Waveguide
10.2 Planar Dielectric Waveguide
10.3 Optical Fibres

10 Waveguides

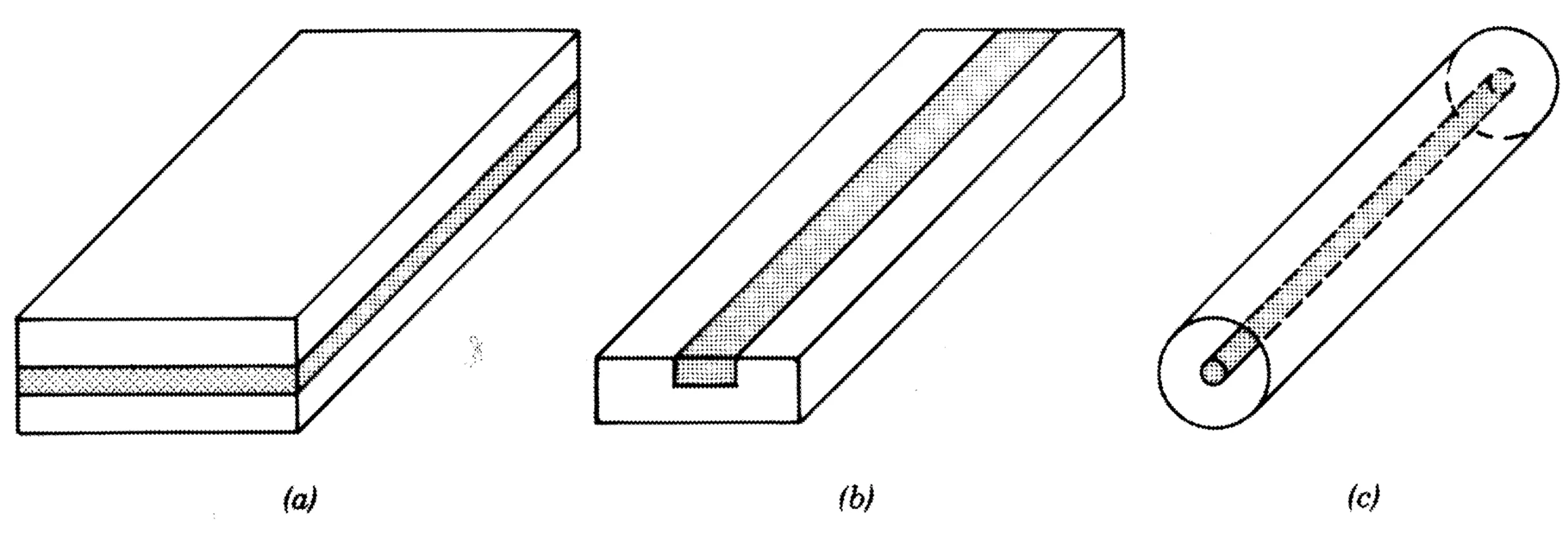
Waveguides are devices that transmit and guide light and other electromagnetic radiation along a prescribed path. In contrast to traditional free-space optics, this guidance occurs within or along a material structure. Waveguides offer the advantage of alignment robustness and, particularly in the case of optical fibres, the ability to circumvent obstructions. They are used extensively in telecommunication over long distances, and also in biomedical applications where light needs to be delivered to or collected from difficult-to-access places. Waveguides are key components of 'integrated optics'. They come in many different forms, as the following figure illustrates:

The difference between the colours in the schematic typically represents different refractive indices. The figure shows, from (a) to (c): a slab waveguide, a strip (or channel) waveguide, and an optical fibre.

10.1 Planar Mirror Waveguide

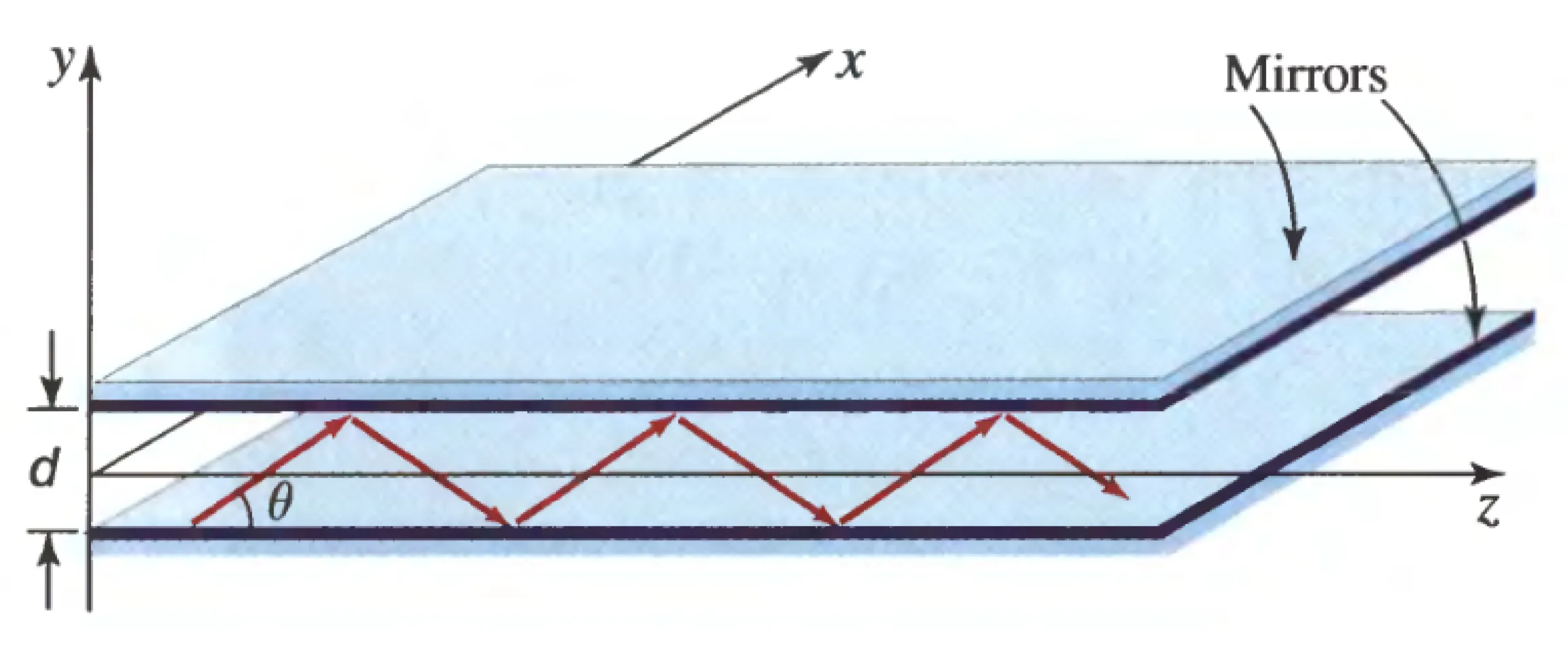
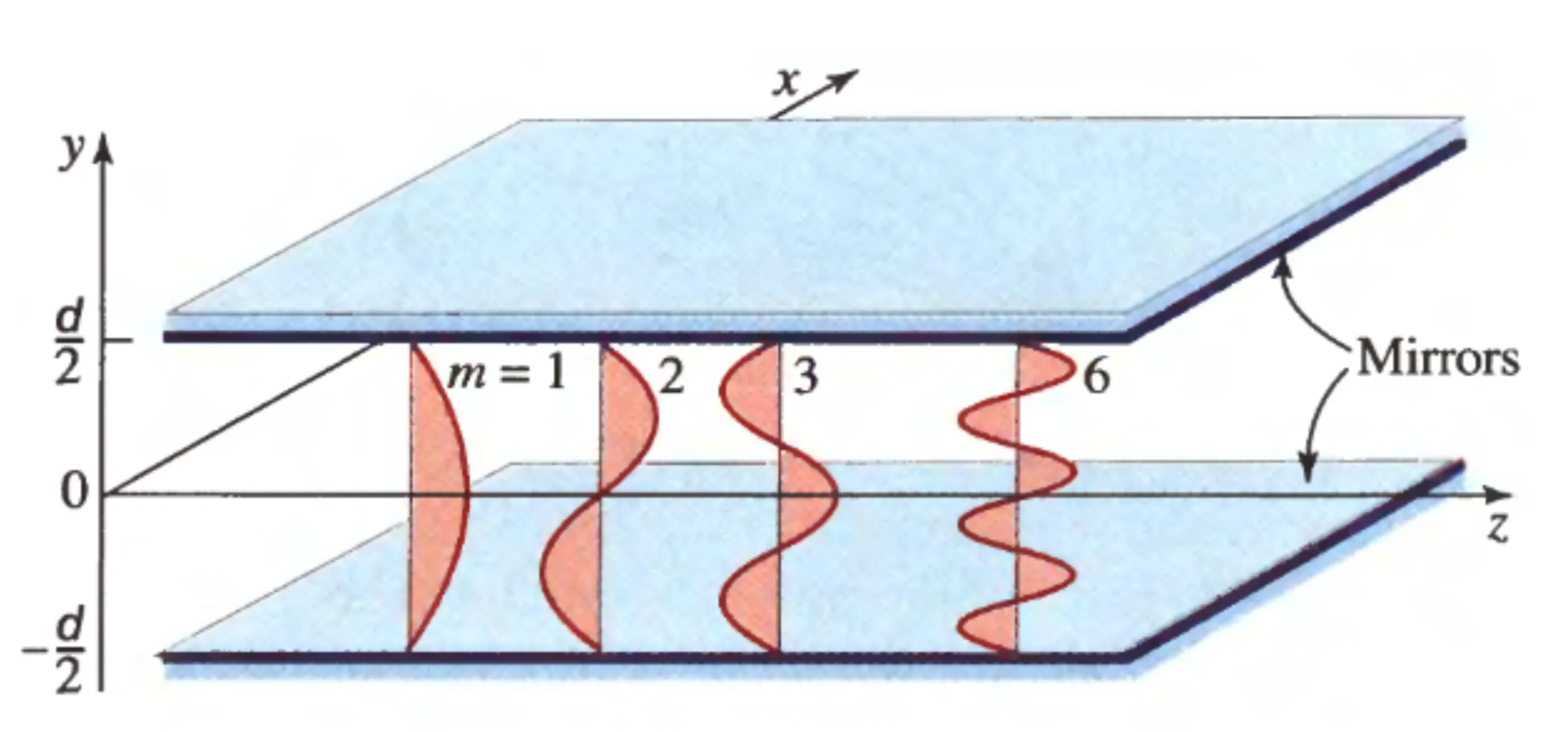
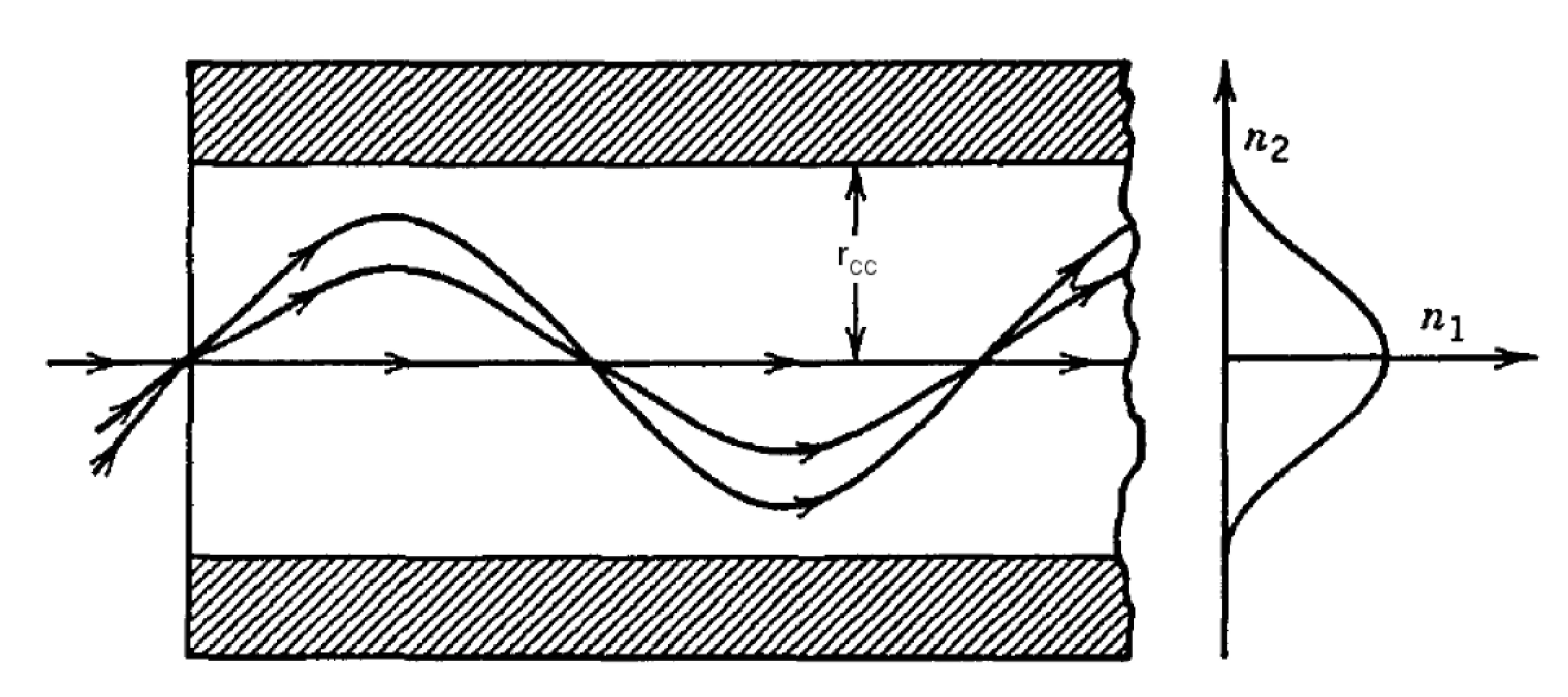
The following figure shows a planar mirror waveguide, consisting of two parallel, highly reflective (ideally perfect) mirrors placed a distance $d$ apart, with a medium of refractive index $n$ between them. While conceptually simple, this is a rather impractical device to construct perfectly. Instead, planar dielectric waveguides based on total internal reflection are commonly used, as discussed later.

One way to treat electromagnetic radiation within this planar mirror waveguide is by using a ray optics picture. We can identify guided modes as those waves that self-consistently interfere (that is, constructively interfere) after undergoing reflections from each mirror. Consider a plane wave bouncing between the mirrors, making an angle $\theta$ with the normal to the mirror surfaces (so it propagates at an angle $({90}^{\circ }-\theta )$ with respect to the waveguide axis, say $z$).

For constructive interference, the phase difference accumulated over one round trip in the transverse ($y$) direction must be an integer multiple of $2\pi$. Considering the path difference between points A and B on a wavefront after one reflection compared to A and C (virtual path), for a wave reflecting between two mirrors separated by $d$: the transverse round trip path difference is $2d\cos \theta$ (if $\theta$ is with surface normal). The phase condition is $k(2d\cos \theta )-2{\varphi }_R=2m\pi$, where ${\varphi }_R$ is phase shift on reflection ( $\pi$ for perfect conductor). This leads to $k_{y}d=m\pi$.
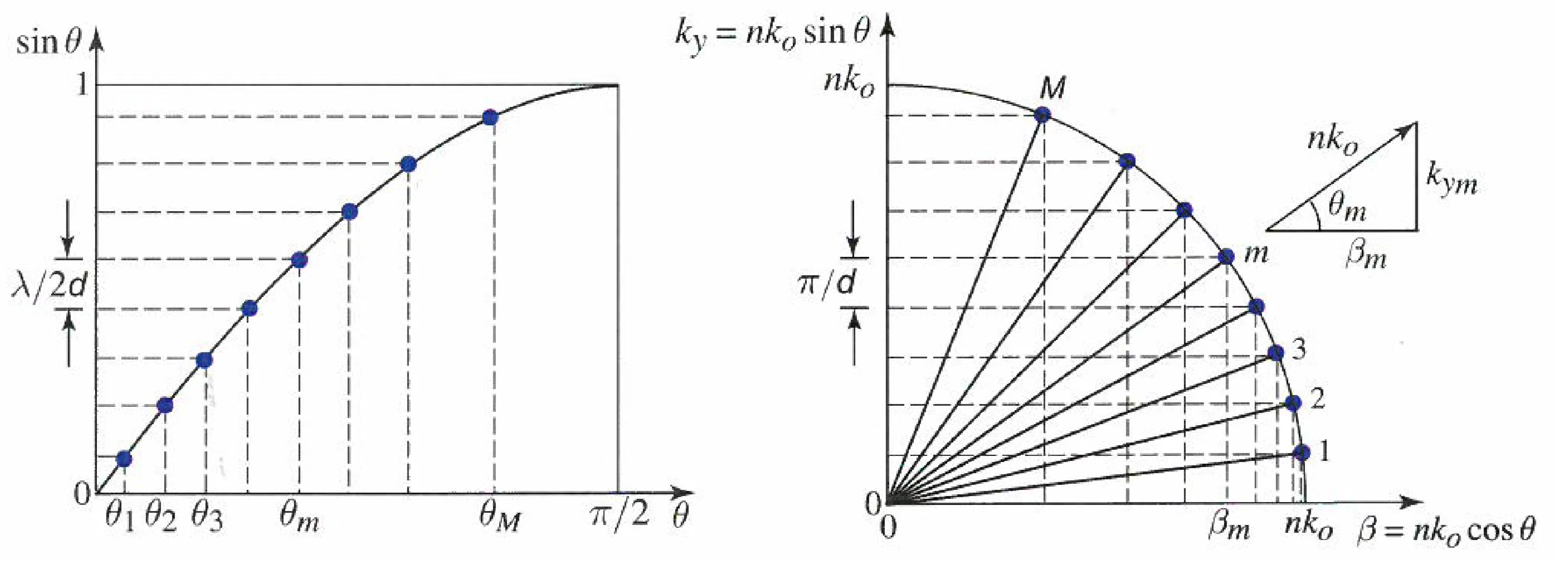
More directly, considering the transverse wavevector component $k_y$: for a wave to be a standing wave in the $y$-direction between $y=0$ and $y=d$ (with field vanishing at boundaries), we need $k_{y}d=m\pi$, where $m$ is a positive integer ($m=1,2,3,\dots$).
The wavevector components are $k_y=k\cos \theta =(n\omega /c)\cos \theta$ and the propagation constant along the waveguide axis (say, $z$) is $\beta =k_z=k\sin \theta =(n\omega /c)\sin \theta$.
From $k_y=m\pi /d$, we have $(n\omega /c)\cos {\theta }_m=m\pi /d$.
The propagation constant for mode $m$ is:

For ${\beta }_m$ to be real (propagating mode), we require $k^2>(m\pi /d{)}^2$, or $\frac{n\omega }{c}>\frac{m\pi }{d}$. This limits the number of modes $m$ that can propagate for a given frequency $\omega$ and waveguide dimension $d$.
Modes of higher order $m$ have a larger $k_y$, thus a larger angle ${\theta }_m$ with respect to the normal (smaller angle with the waveguide axis $z$). They undergo more reflections per unit length and their effective propagation velocity along $z$ is lower.

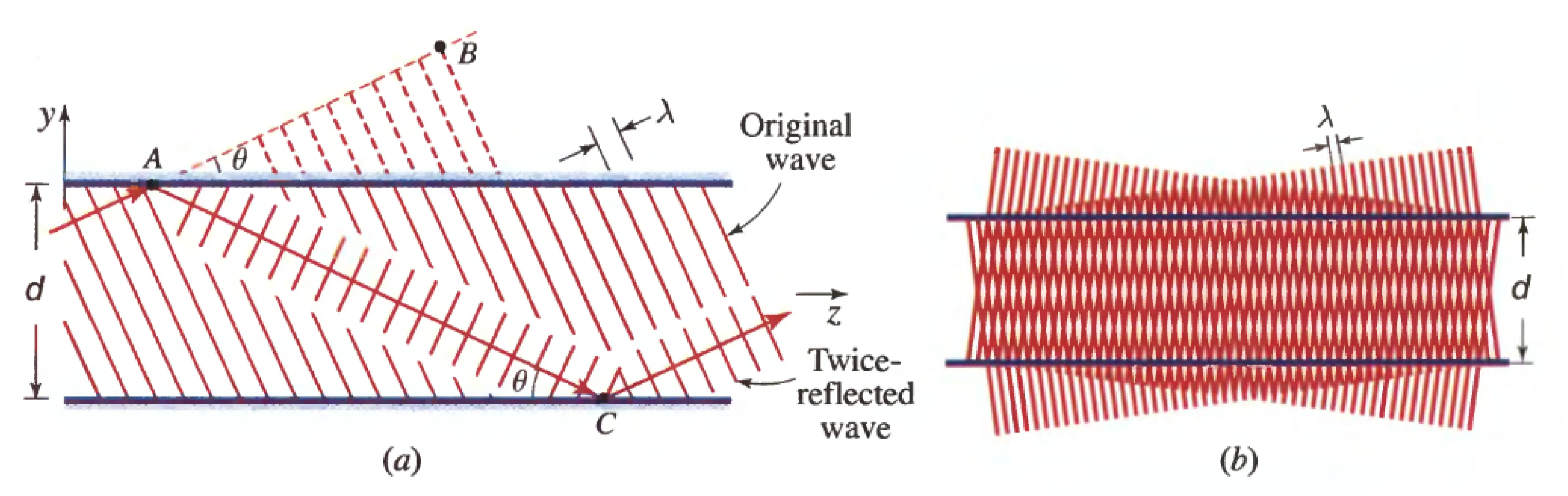
Alternatively, considering a superposition of two plane waves with wavevectors ${\mathbf{k}}_1=(k_x,k_y,\beta )$ and ${\mathbf{k}}_2=(k_x,-k_y,\beta )$ (assuming 2D $y,z$ propagation for simplicity, $k_x=0$). The total field must satisfy boundary conditions, for instance, tangential $E$-field must be zero at perfect conductor surfaces $y=\pm d/2$.
Let $E(y,z,t)=\mathfrak{Re}[E_1{e}^{i(\omega t-k_{y}y-\beta z)}+E_2{e}^{i(\omega t+k_{y}y-\beta z)}]$.
Boundary conditions $E(y=\pm d/2)=0$ for all $z,t$ lead to $E_1{e}^{-i{k}_{y}d/2}+E_2{e}^{i{k}_{y}d/2}=0$ and $E_1{e}^{i{k}_{y}d/2}+E_2{e}^{-i{k}_{y}d/2}=0$.
These require either $E_1=-E_2$ and $\sin (k_{y}d/2)=0⟹k_{y}d/2=m^{\prime }\pi ⟹k_y=2m^{\prime }\pi /d$ (even modes for $E(y)$ about $y=0$),
or $E_1=E_2$ and $\cos (k_{y}d/2)=0⟹k_{y}d/2=(m^{\prime }-1/2)\pi ⟹k_y=(2m^{\prime }-1)\pi /d$ (odd modes for $E(y)$ about $y=0$).
Combining these, $k_y=m\pi /d$ for $m=1,2,3,\dots$.

10.1.1 TE Modes

For Transverse Electric (TE) modes, the electric field is transverse to the direction of propagation $z$, so $E_z=0$. If we assume $\mathbf{E}=\hat{\mathbf{x}}{E}_x(y,z,t)$, then $E_x$ must satisfy the boundary conditions. The superposition results in field patterns:

where $f_m(y)$ are sine or cosine functions satisfying the boundary conditions:

• $f_m(y)=\sin (m\pi y/d)$ for $m=1,2,3,\dots$ (if boundaries at $y=0,d$)
• $f_m(y)=\cos (m\pi y/d)$ for odd $m=1,3,\dots$ (symmetric modes about $y=0$, boundaries at $\pm d/2$)
• $f_m(y)=\sin (m\pi y/d)$ for even $m=2,4,\dots$ (antisymmetric modes about $y=0$, boundaries at $\pm d/2$)

Odd modes ($m=1,3,5,...$): $E_x\sim \cos (m\pi y/d)$, non-zero intensity at centre.
Even modes ($m=2,4,6,...$): $E_x\sim \sin (m\pi y/d)$, zero intensity (node) at centre.
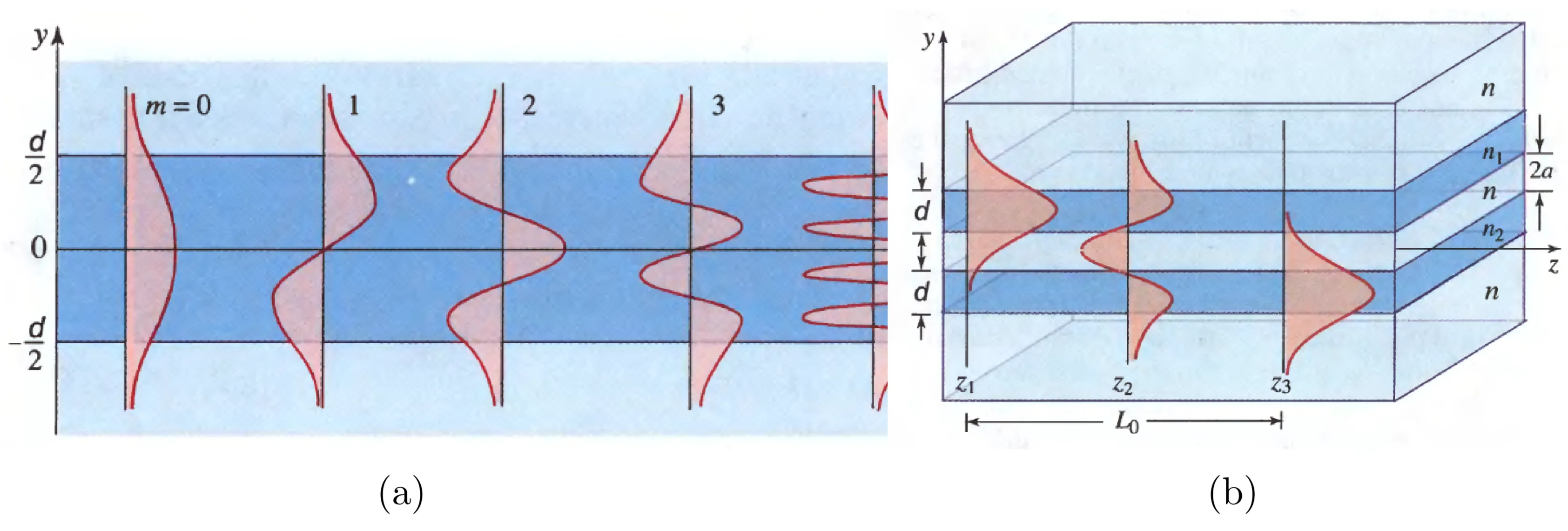
This is shown in the following figure (assuming $E_x$ component):

The associated magnetic field will have a non-zero $z$-component for these TE modes. The larger the mode number $m$, the smaller the propagation constant ${\beta }_m$ for a given $\omega$, meaning the phase fronts for that mode propagate more slowly along $z$.
Planar mirror waveguides support a finite number of propagating modes $M$ for a given wavelength $\lambda ={\lambda }_0/n$:

Thus, for a sufficiently thin waveguide ($d<{\lambda }_0/(2n)$), only a single mode ($m=1$, if allowed by geometry for TE/TM distinction) or no modes can propagate. Each mode $m$ has a cutoff frequency ${\nu }_{c,m}=mc/(2nd)$ (or wavelength ${\lambda }_{c,m}=2nd/m$), below which ($\nu <{\nu }_{c,m}$ or $\lambda >{\lambda }_{c,m}$) that mode cannot propagate (${\beta }_m$ becomes imaginary).

10.1.2 TM Modes

For Transverse Magnetic (TM) modes, the magnetic field is transverse to $z$ ($H_z=0$), so the electric field must have a $z$-component ($E_z\ne 0$). The boundary conditions for perfect conductors require tangential $\mathbf{E}$ to be zero and normal $\mathbf{B}$ to be zero. For TM modes, $H_x$ is the tangential component. The treatment is analogous to TE modes, leading to the same discretisation of $k_y$ and the same dispersion relation for ${\beta }_m$. The field profiles differ:
For $m$ odd ($H_x\sim \cos (m\pi y/d)$ if origin at centre):

For $m$ even ($H_x\sim \sin (m\pi y/d)$ if origin at centre):

The exact coefficients and signs depend on normalisation and specific field component definitions. Thus, for each mode number $m$, there generally exists both a TE and a TM-polarised version with the same propagation constant ${\beta }_m$ in this idealised structure.

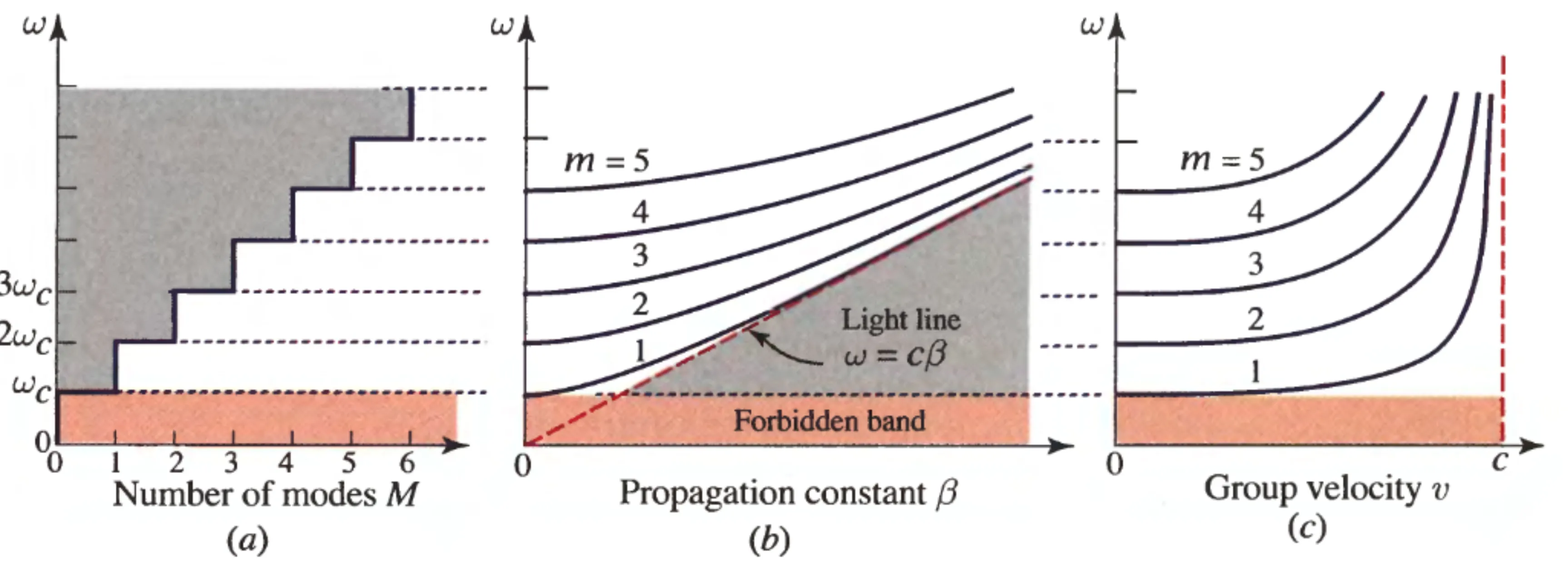
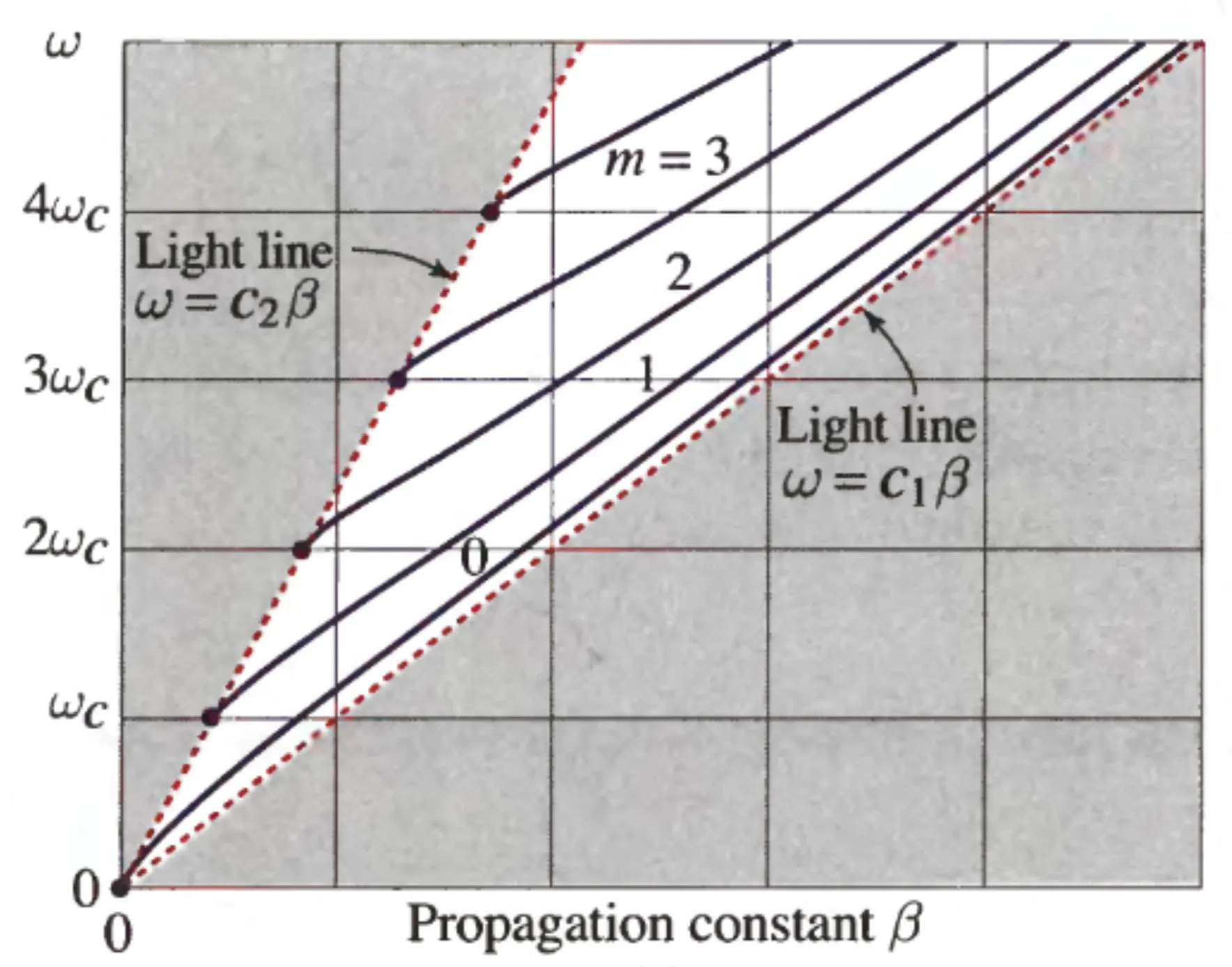
10.1.3 Dispersion Relation

The propagation constant ${\beta }_m$ can be written in terms of a cutoff frequency ${\omega }_{c,m}=m\pi c/(nd)$ for each mode $m$:

This is the dispersion relation for the $m$-th mode. This is shown in the next figure ($\omega$ vs $\beta$):

We observe in (b) that dispersion diagrams for different modes $m$ yield similar curves in the $\omega -\beta$ space, each starting at its respective cutoff frequency ${\omega }_{c,m}$. For a fixed $\beta$, higher-order modes require a higher frequency to have the same propagation constant. For large values of $\omega$ (far above cutoff), ${\beta }_m\approx n\omega /c=n{k}_0$, approaching the "light line" of the material filling the waveguide core. This light line represents the dispersion relation of plane waves in a homogeneous medium with refractive index $n$. If ${\beta }_m$ were to fall outside this light cone (so ${\beta }_m>n{k}_0$), it would imply an imaginary transverse wavevector component even within the core, which is not typical for these guided modes. If $\omega <{\omega }_{c,m}$, ${\beta }_m$ becomes imaginary, meaning the mode is evanescent (non-propagating). Due to the perfect mirrors in our treatment, no evanescently decaying field is possible outside the mirrors (as fields are zero there), but modes below cutoff do not propagate.

An effective refractive index $n_{m,\text{eff}}$ can be associated with each mode:

where $k_0=\omega /c$ is the vacuum wave number.

10.1.4 Group and Phase Velocity

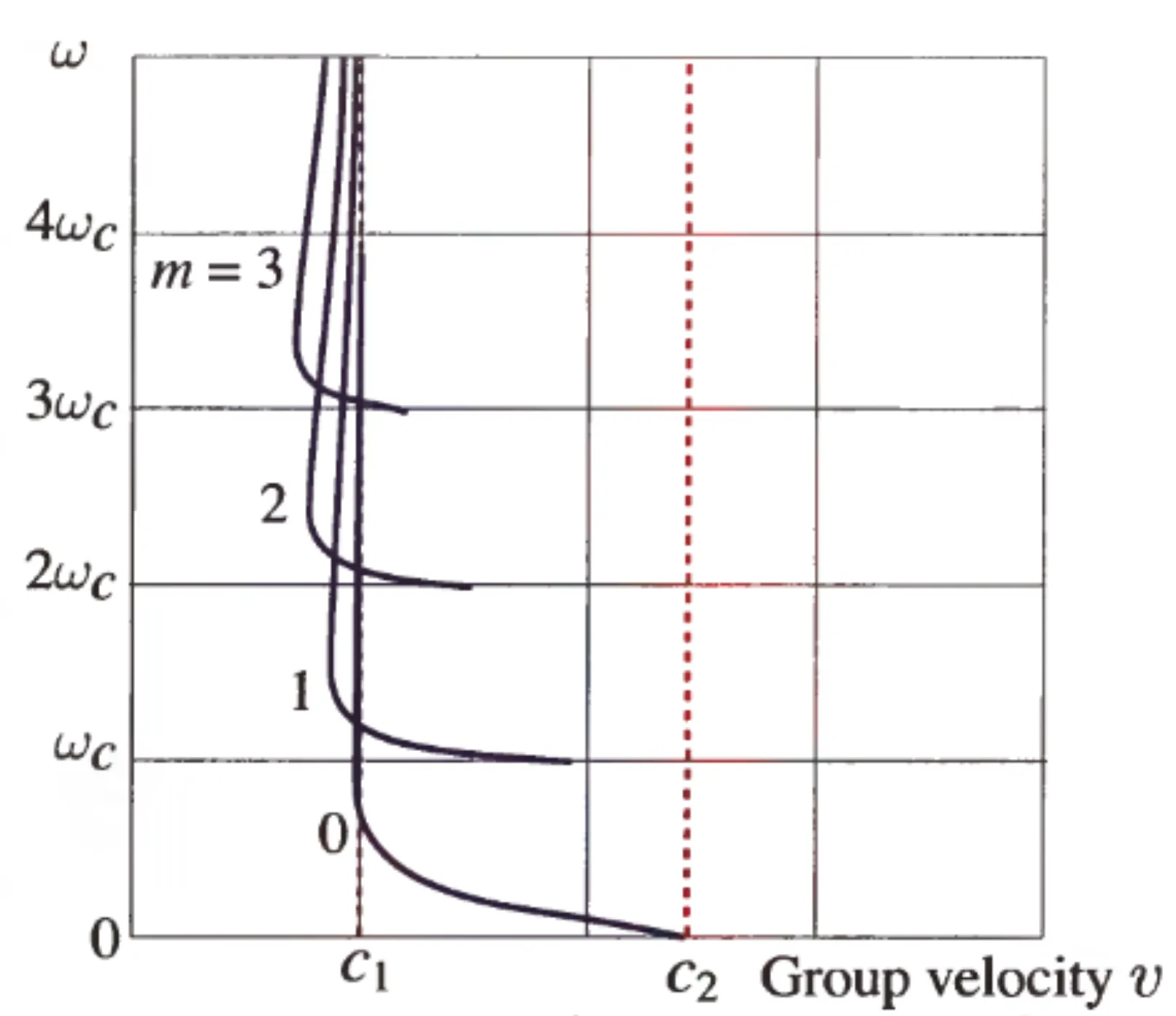
The group velocity $v_{g,m}$ for mode $m$ is the speed of energy or information propagation for that mode:

where $\cos {\theta }_m={\beta }_m/(n{k}_0)$ defines the angle of the constituent plane waves with the $z$-axis. Geometrically, it is the projection of the plane wave velocity $c/n$ onto the waveguide axis. The group velocity is always less than or equal to $c/n$ and decreases for higher mode numbers $m$ (at a fixed frequency) or as $\omega$ approaches ${\omega }_{c,m}$.
The phase velocity for mode $m$ is:

Since $n_{m,eff}<n$, $v_{p,m}>c/n$.

10.1.5 Multimode Fields

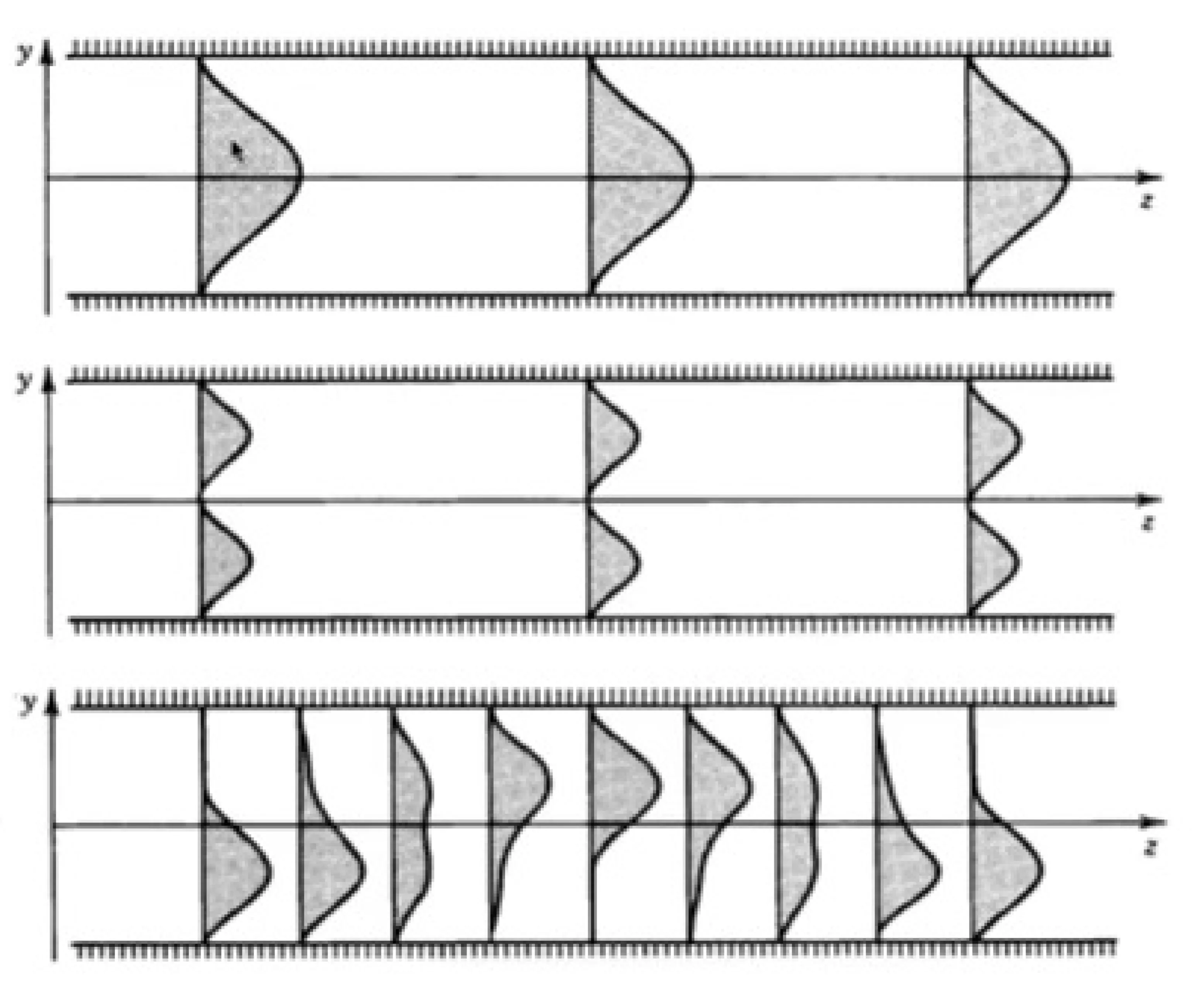
Generally, any field distribution that satisfies the boundary conditions (vanishes at the mirrors) will be guided. Such arbitrary fields can be expressed as a linear superposition of the allowed TE and TM modes. The transverse field profile of an arbitrary guided waveform will evolve with propagation distance $z$ due to the different phase velocities (and group velocities, leading to modal dispersion) of the underlying modes.

10.2 Planar Dielectric Waveguide

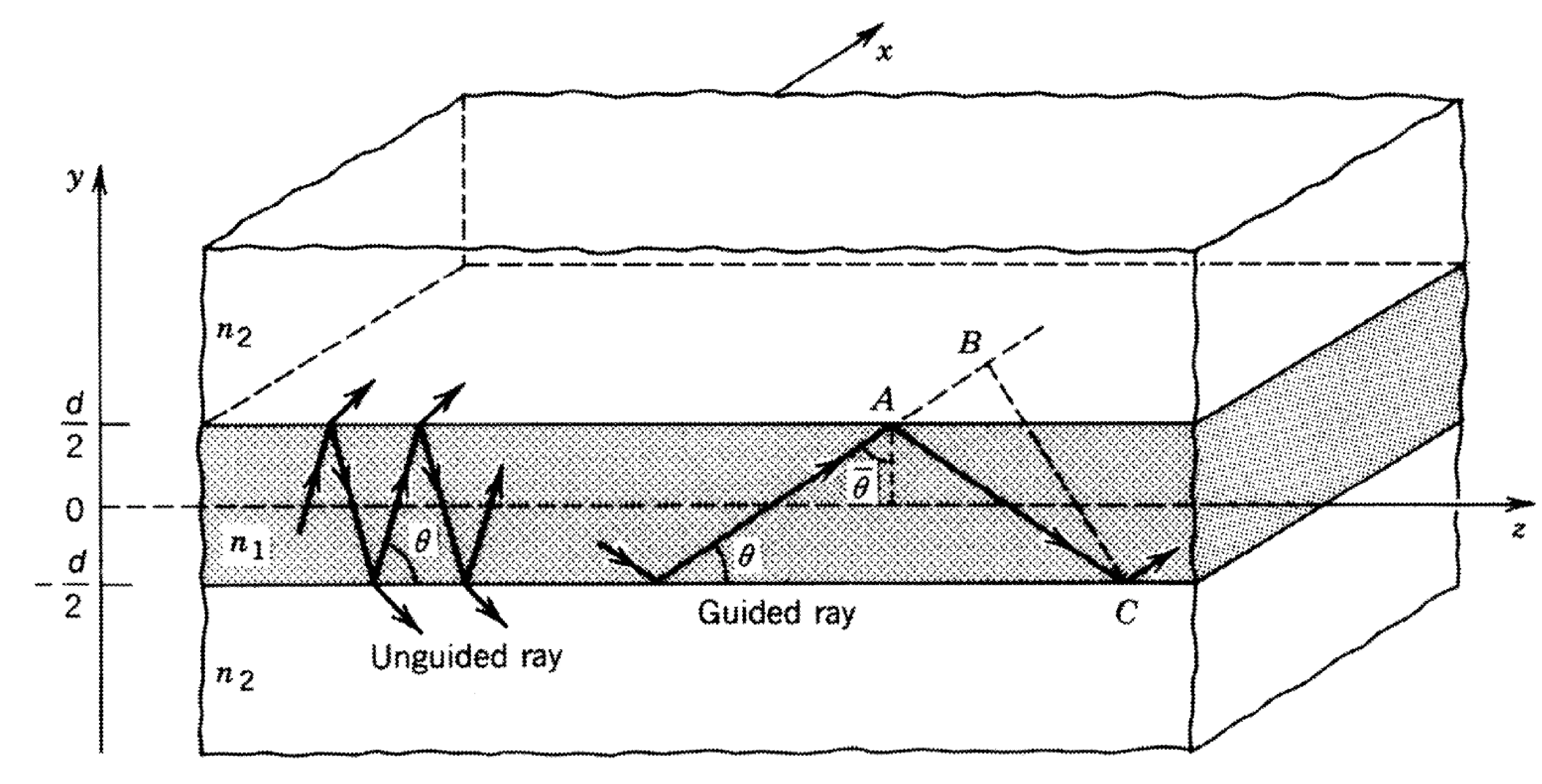
Planar waveguides are practically implemented using transparent dielectric materials with generally differing refractive indices. A common structure is a slab waveguide, consisting of a core layer with refractive index $n_1$ and thickness $d$, surrounded by cladding layers with a lower refractive index $n_2$ (i.e., $n_1>n_2$).

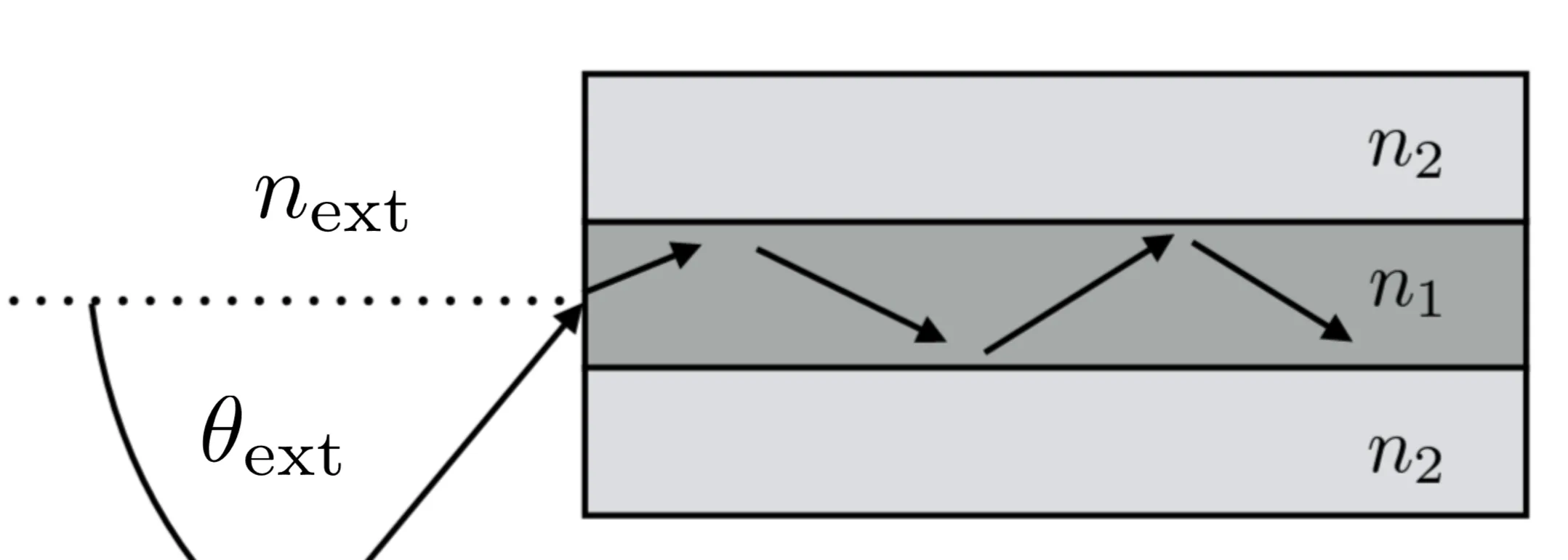
Light is guided within the core by total internal reflection (TIR) at the core-cladding interfaces. Rays incident on the interface from within the core at an angle ${\theta }_1$ (with respect to the normal) greater than the critical angle ${\theta }_c=\arcsin (n_2/n_1)$ will be totally reflected.
Similarly to the mirror waveguide, we seek self-consistent modes. However, an important difference is that upon total internal reflection, the reflected beam experiences a phase shift ${\varphi }_r$ which is not simply $\pi$ (as for a perfect conductor) but depends on the angle of incidence ${\theta }_1$ and the polarisation (TE or TM). For TE modes, this phase shift is given by:

A wave trapped within the waveguide core experiences this phase shift at each reflection. The condition for a guided mode is that the total phase change over a round trip in the transverse direction (including reflection phases) must be an integer multiple of $2\pi$. This leads to a transcendental equation for the allowed propagation angles ${\theta }_1$ (or transverse wave numbers $k_{y1}=n_1{k}_0\cos {\theta }_1$):

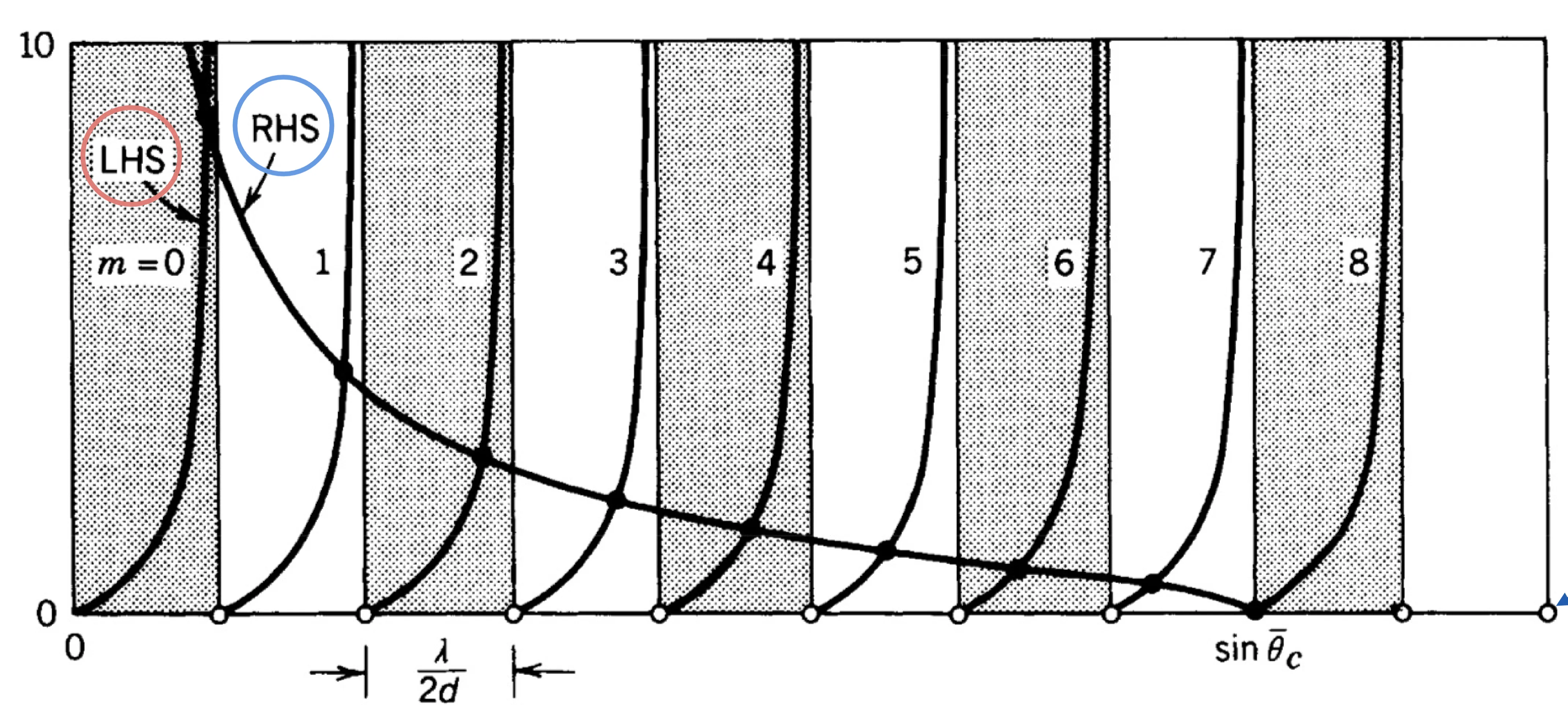
These equations are difficult to solve analytically and are typically solved graphically or numerically:

There is a finite number $M$ of guided modes, limited by the condition that ${\theta }_1$ must be greater than ${\theta }_c$ for TIR. The approximate number of TE modes is:

This leads to a cutoff condition for each mode. The fundamental mode (m=0 for TE, in symmetric slab) has no cutoff frequency if $d>0$. TM modes have similar, but slightly different, eigenvalue equations due to a different TIR phase shift.
The dispersion diagram for a dielectric slab waveguide shows modes confined between the light line of the cladding ($k_0{n}_2$) and the light line of the core ($k_0{n}_1$):

The effective refractive index $n_{\text{eff},m}={\beta }_m/k_0$ for guided modes lies between $n_2<n_{\text{eff},m}<n_1$. It must be larger than $n_2$ for TIR to occur, and smaller than $n_1$ as some field exists in the cladding.
The group velocity $v_g=d\omega /d\beta$ can be calculated from the dispersion relation:

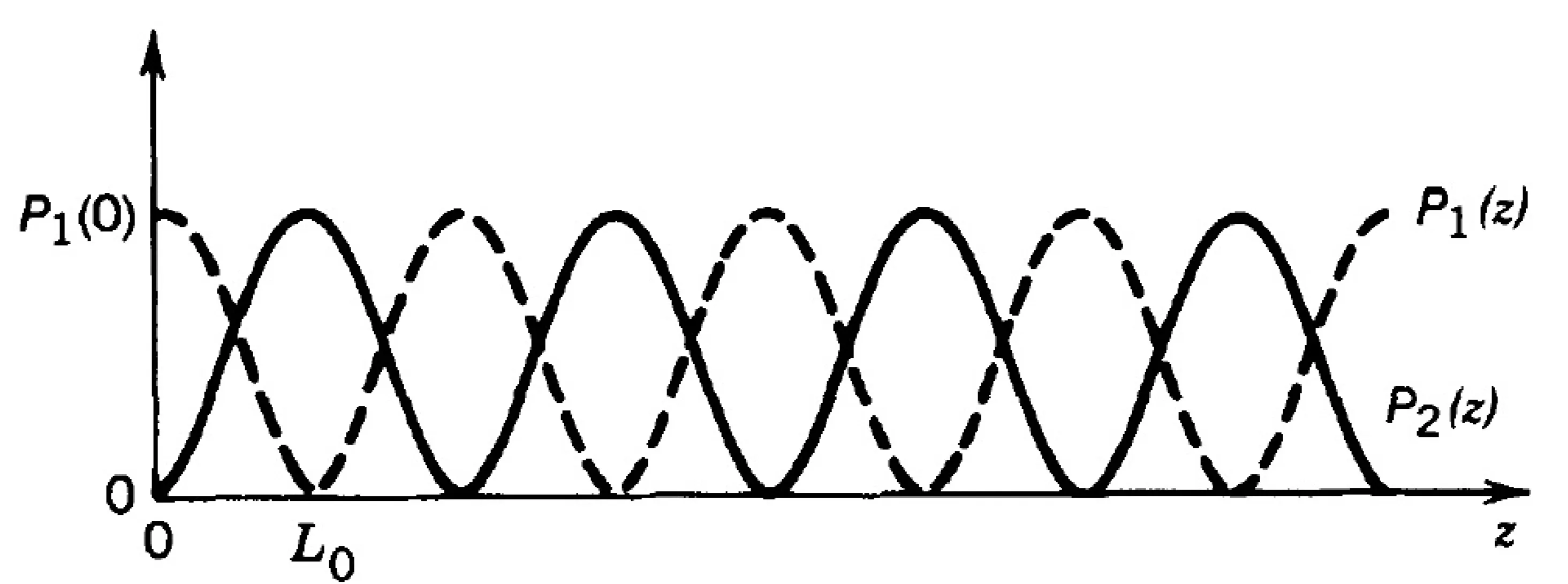
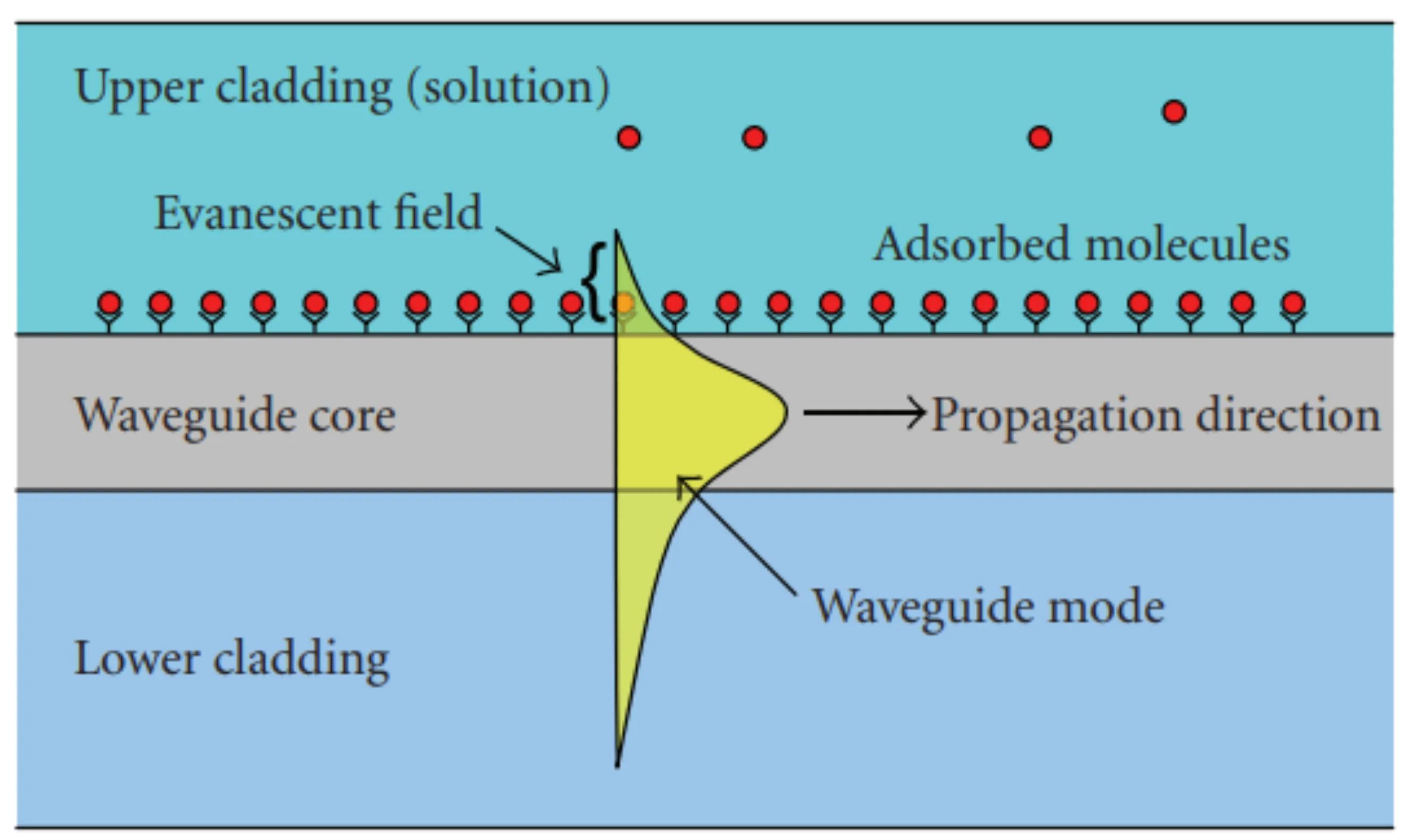
A key feature of dielectric waveguides is the presence of evanescent tails of the guided modes extending into the cladding region, even under TIR conditions. The field in the cladding decays exponentially with distance from the interface. This allows for evanescent field coupling if another waveguide is brought sufficiently close:

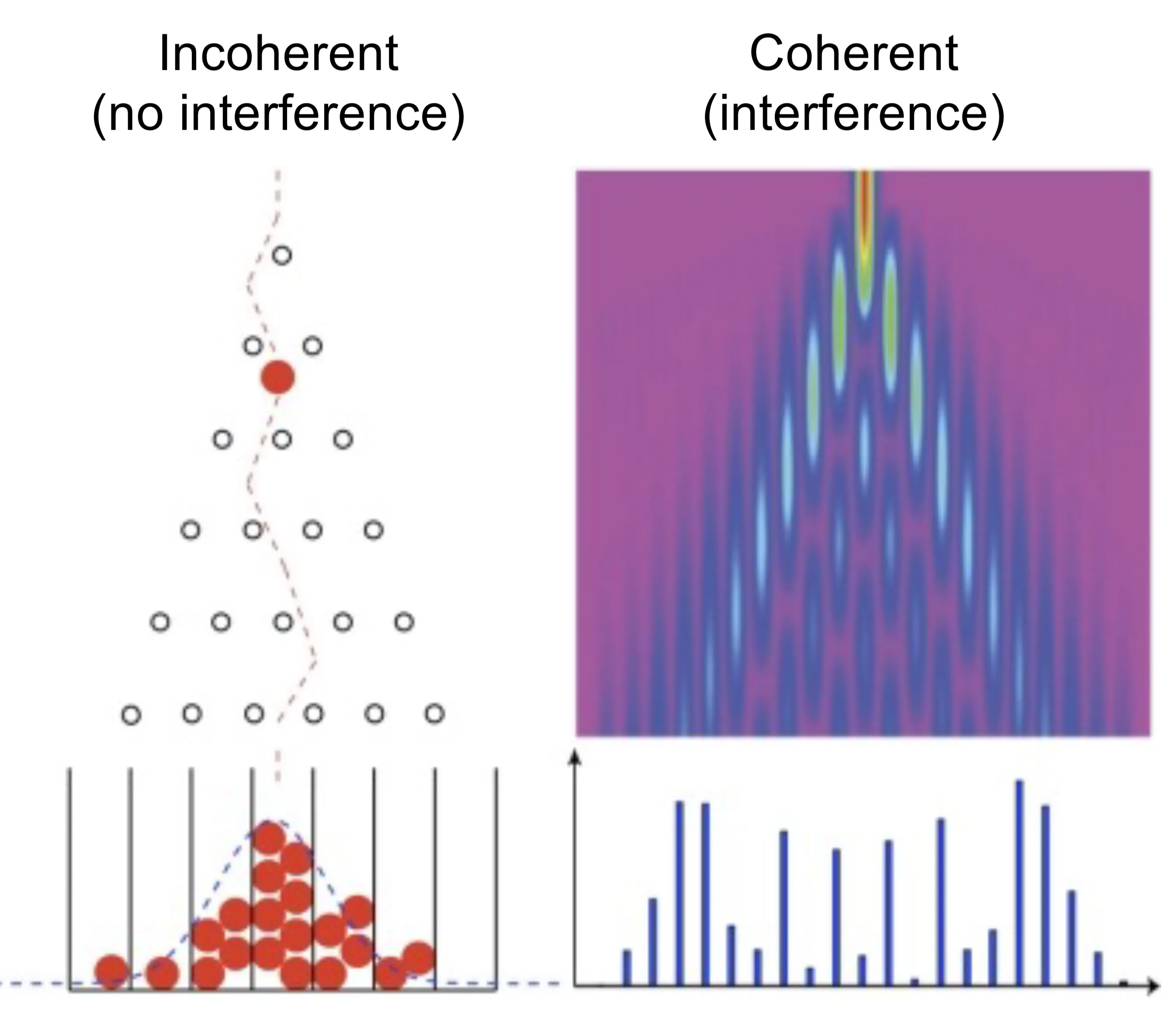
This coupling causes optical power to oscillate periodically between the two waveguides, forming the basis of directional couplers, which act as beamsplitters or power taps in integrated optics. Evanescently coupled waveguide arrays can also demonstrate coherence properties of light and are used in sensing applications, where changes in the cladding medium near the surface (such as binding of molecules) alter the effective index of the guided mode, leading to a measurable phase shift.

10.2.1 Numerical Aperture

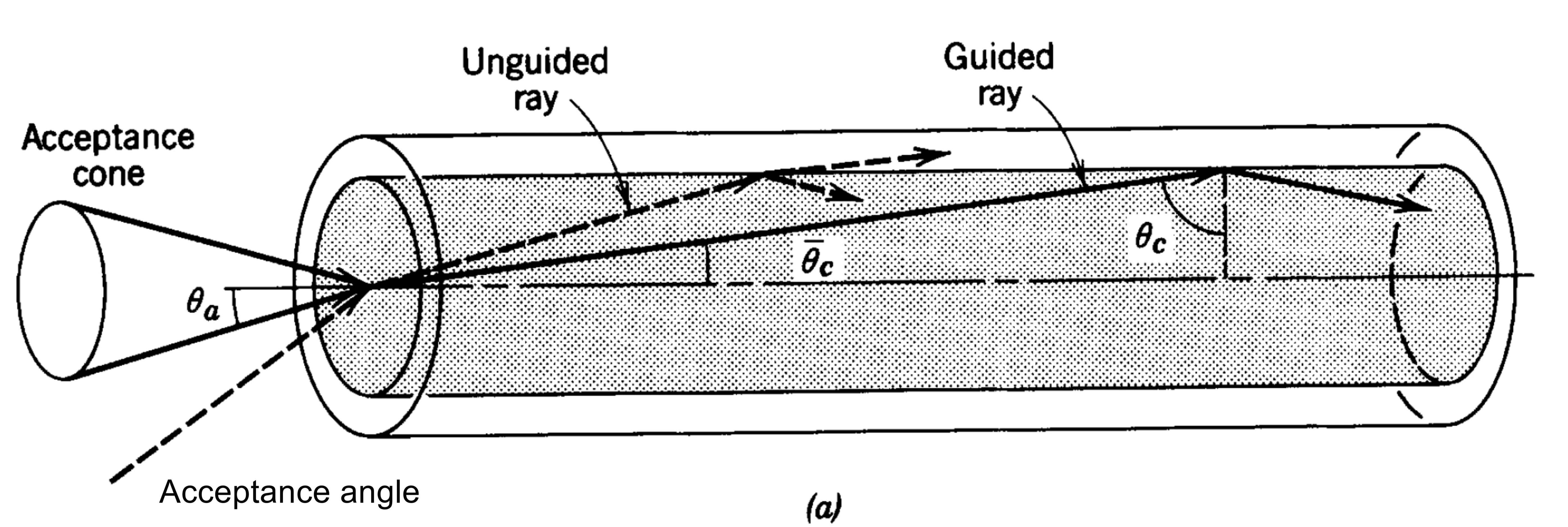
The numerical aperture (NA) is a measure of the light-gathering ability of an optical system, including waveguides. For a waveguide, it defines the maximum acceptance angle ${\theta }_{\text{acc}}$ for light incident from an external medium (refractive index $n_{\text{out}}$) to be coupled into guided modes:

For a planar dielectric slab waveguide with core index $n_1$ and cladding index $n_2$, the NA is given by:

This determines the cone of acceptance for efficient input coupling and also the divergence cone of light exiting the waveguide into free space.

10.2.2 Integrated Waveguides

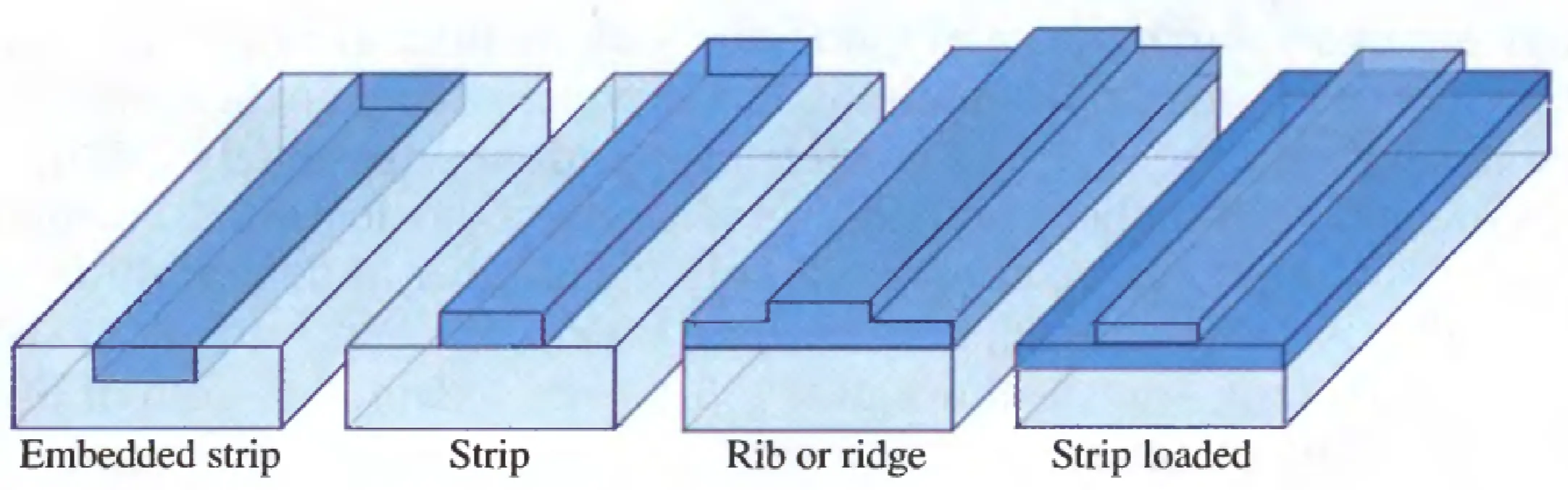
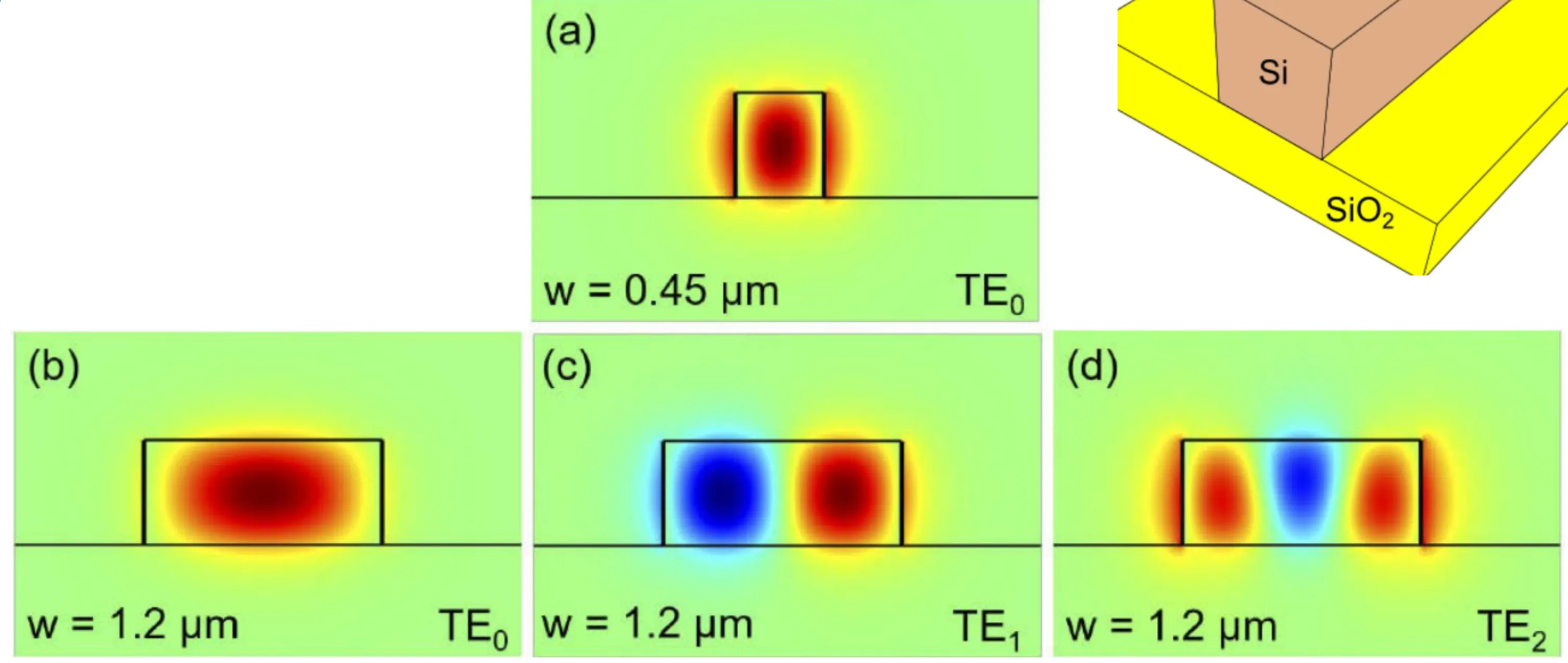
A rapidly growing field in photonics is integrated optics, aiming to create compact optical circuits on a chip that guide, modulate, switch, and process light signals. These are often based on dielectric strip or channel waveguides.

Higher refractive index contrast between the core and cladding allows for stronger mode confinement, enabling tighter bends and more compact device footprints. The image below shows different modes that can be confined in a strip waveguide made of Si on SiO${}_2$, depending on wavelength and dimensions.

10.3 Optical Fibres

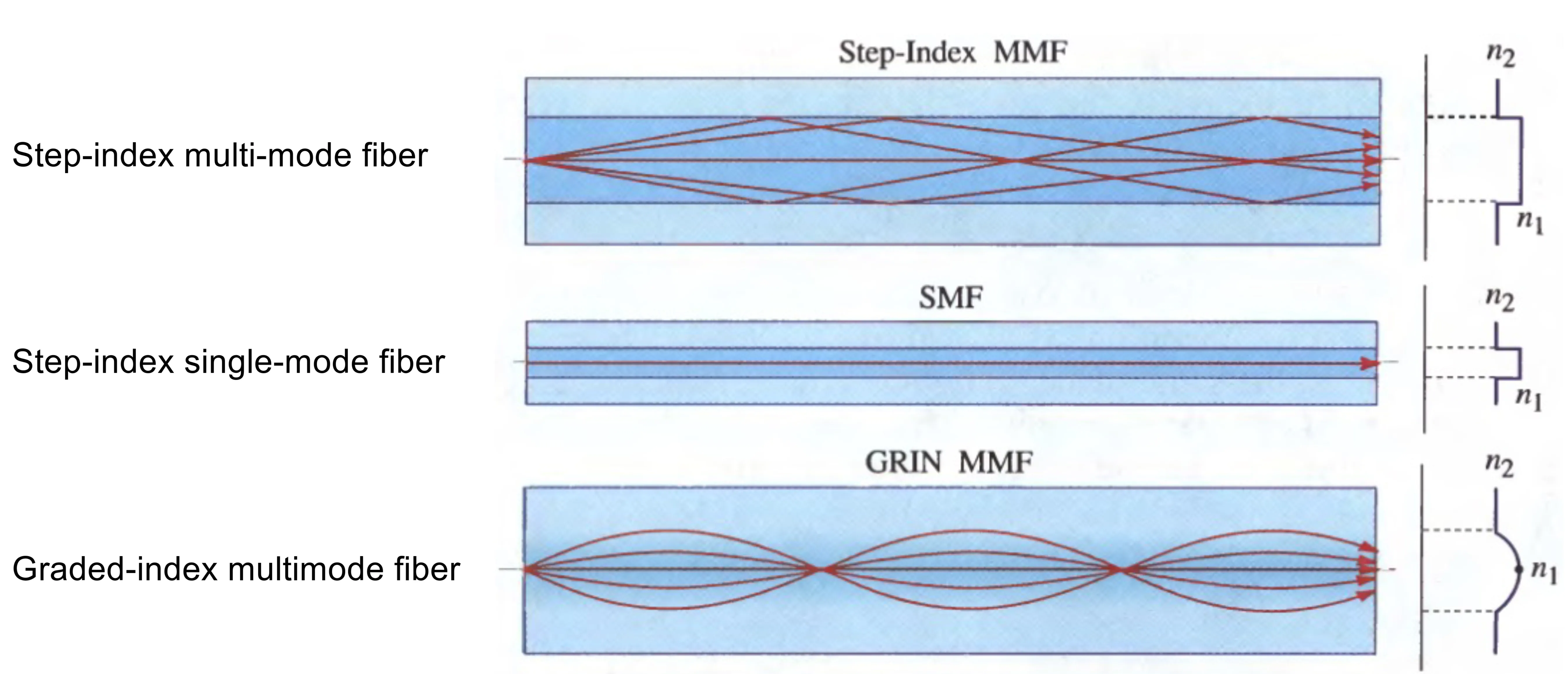
Optical fibres are a crucial class of cylindrical waveguides, essential for long-distance telecommunication and many other applications. Most common are step-index fibres, where a cylindrical core of higher refractive index $n_1$ is surrounded by a cladding of lower refractive index $n_2$.

The refractive index difference $(n_1-n_2)/n_1$ is typically very small (around 1% or less for standard telecommunication fibres) but sufficient for low-loss waveguiding via TIR. For instance, a silica ($n_{\text{SiO2}}\approx 1.44$) cladding might surround a germanium-doped silica core ($n_{\text{core}}\approx 1.46$).
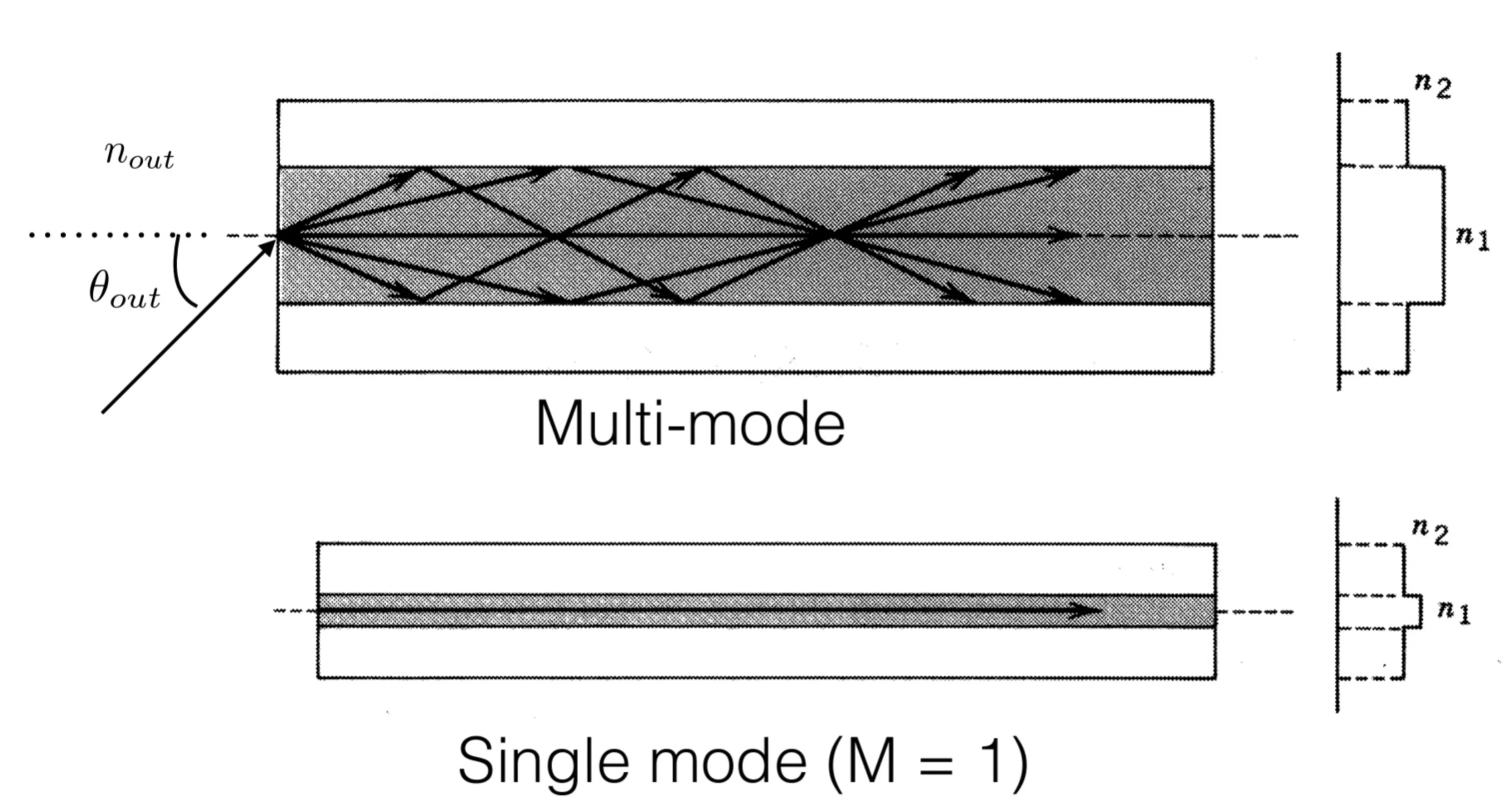
The guiding principle is total internal reflection at the core-cladding interface for rays incident at sufficiently grazing angles. The number of guided modes depends on the core diameter $2a$, the wavelength ${\lambda }_0$, and the NA.

• Single-mode fibres (SMFs) are designed with a small core diameter to support only the fundamental mode (typically $H{E}_{11}$) for a given wavelength.
• Multi-mode fibres (MMFs) have larger cores and support many modes.
  The output of an SMF is approximately Gaussian in its transverse profile, which is beneficial for beam quality. MMFs suffer from modal dispersion (different modes travel at different group velocities), which limits their bandwidth for long-distance communication.

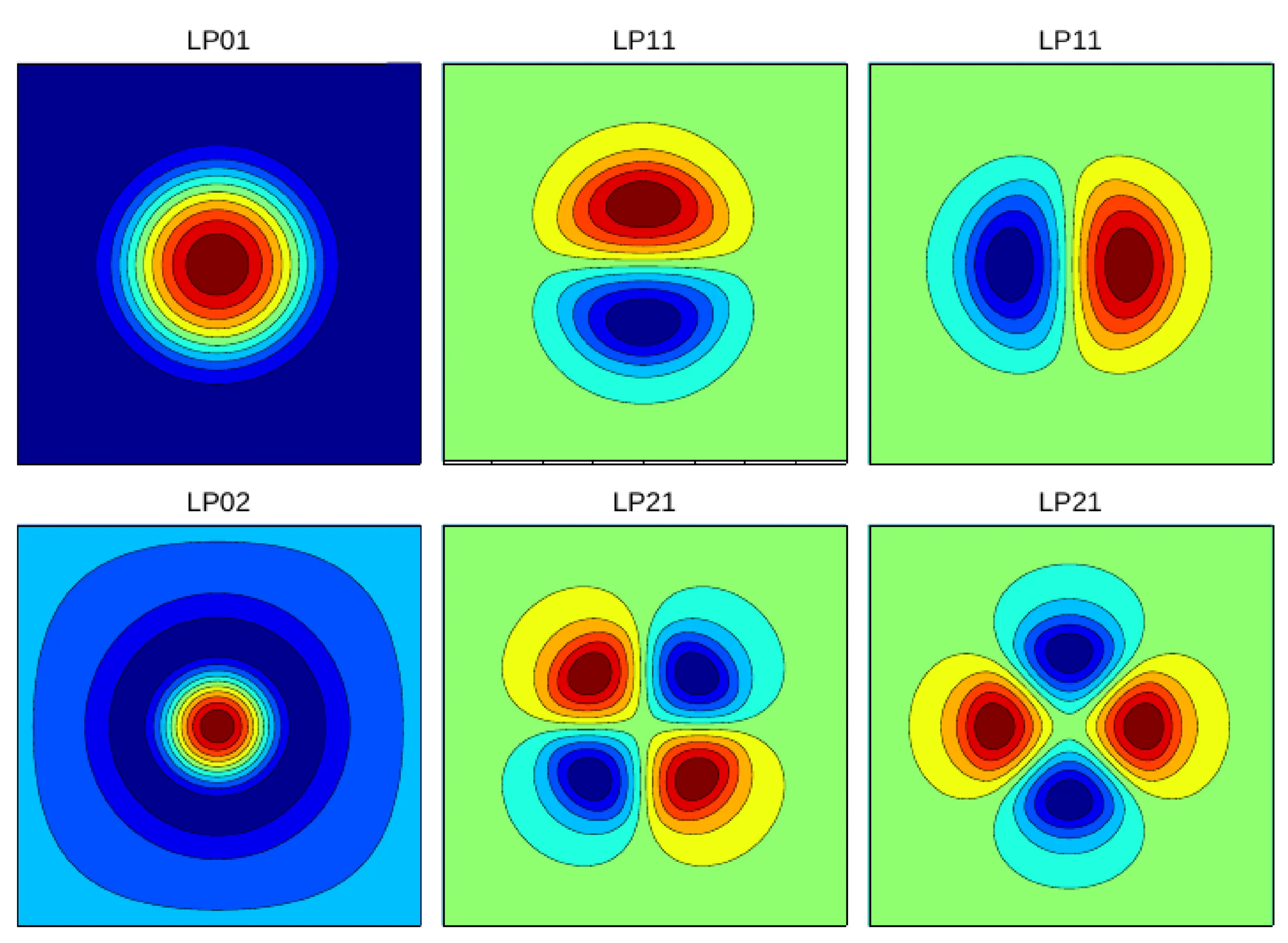
The field distributions for the lowest-order modes in a step-index optical fibre are described by Bessel functions in the core and modified Bessel functions in the cladding. Under the weak guiding approximation ($\mathrm{\Delta }=(n_1-n_2)/n_1\ll 1$), these modes can be simplified to Linearly Polarised (LP) modes. For larger index contrast, one must distinguish between TE, TM, and hybrid (HE, EH) modes, the latter having both non-zero longitudinal $E_z$ and $H_z$ components.

A fibre is single-mode if the normalised frequency or V-parameter satisfies:

where $a$ is the core radius and $\mathrm{NA}=\sqrt{n_1^2-n_2^2}$. Therefore, a small core diameter and small NA promote single-mode operation. Shorter wavelengths make single-mode operation more difficult for a given fibre.

Analogous to the planar dielectric waveguide, light from outside is accepted into the fibre if its angle of incidence ${\theta }_{\text{in}}$ (in the external medium of index $n_{\text{ext}}$) satisfies $n_{\text{ext}}\sin {\theta }_{\text{in}}<\mathrm{NA}$. The NA is typically $0.1$ to $0.25$ for standard fibres, corresponding to acceptance half-angles of $5^{\circ }$ to ${15}^{\circ }$ in air ($n_{\text{ext}}=1$).

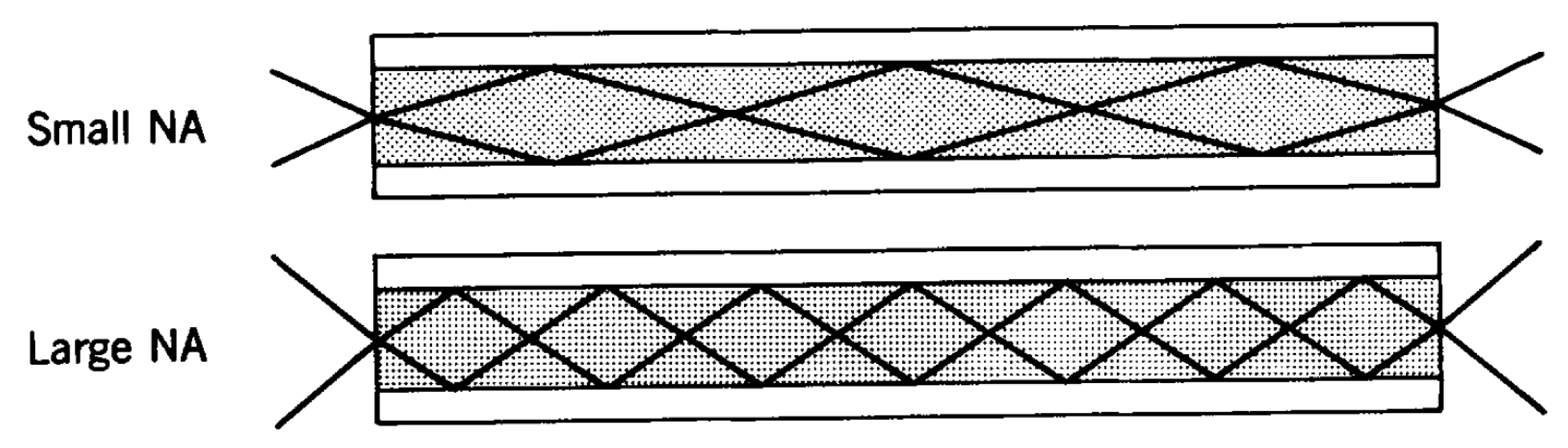
A large NA corresponds to a wider acceptance cone, making it easier to couple light into the fibre, but often implies higher potential for modal dispersion in MMFs or different guiding properties.

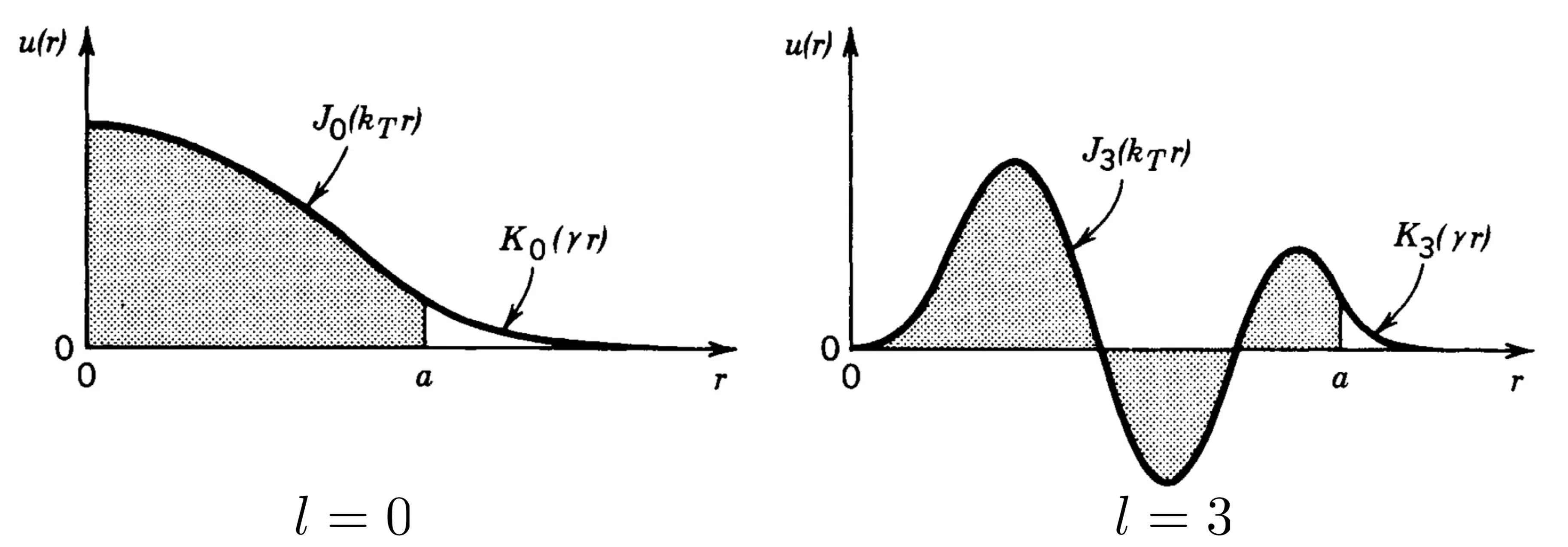
The radial part of the field solutions $u(r)$ in a fibre with core radius $a$ behave as:

where $J_l$ is a Bessel function of the first kind, $K_l$ is a modified Bessel function of the second kind (which decays for $r\to \mathrm{\infty }$), $k_T^2=n_1^2{k}_0^2-{\beta }^2$ (transverse wave number in core), and ${\gamma }^2={\beta }^2-n_2^2{k}_0^2$ (decay constant in cladding).

10.3.1 Graded-Index Fibres

Another type of optical fibre is the graded-index fibre (GRIN fibre), where the refractive index of the core $n_1(r)$ varies continuously (typically parabolically) from a maximum value at the centre ($r=0$) to the value of the cladding index $n_2$ at the core-cladding boundary. GRIN fibres are more complex to manufacture but can significantly reduce modal dispersion compared to step-index MMFs. This is because rays (or modes) taking longer, more helical paths also travel through regions of lower average refractive index, thus increasing their speed, which can equalise travel times for different modes.

Typically, optical fibres also include an outer protective coating or 'jacket' for mechanical strength and protection.

10.3.2 Fibre Losses

For telecommunication applications transmitting signals over many thousands of kilometres, minimising fibre losses is crucial. Typically, a constant intrinsic loss coefficient $\alpha$ (in units of, for instance, dB/km) is considered. The optical power $P(z)$ transmitted through a fibre of length $z$ is described by:

where ${\alpha }^{\prime }$ is the linear attenuation coefficient (units of ${\text{m}}^{-1}$ or ${\text{km}}^{-1}$).
The attenuation coefficient ${\alpha }^{\prime }({\lambda }_0)$ is frequency-dependent (dispersive) and arises from several sources:

• Material absorption: Intrinsic absorption in the fibre material (such as silica), particularly from OH- ion impurities or UV/IR absorption tails.
• Rayleigh scattering: Scattering from microscopic density fluctuations frozen into the glass structure, scaling as $1/{\lambda }_0^4$. This is dominant at shorter visible/near-IR wavelengths.
• Waveguide imperfections / Mie scattering: Scattering from imperfections at the core-cladding interface or from larger-scale refractive index variations.
• Bending losses: Radiative losses incurred when the fibre is bent too tightly.
• Interface/Coupling losses: Losses at connections between fibres or to other optical elements.

Since losses often involve exponential power drop, decibel (dB) units are commonly used:

where ${\alpha }_{\text{dB}}$ is the loss in dB/km. A factor of $1/2$ power loss corresponds to approximately $3\text{dB}$ loss, while a factor of $1/10$ corresponds to $10\text{dB}$ loss. Optical power is also often expressed in dBm, referenced to $1\text{mW}$:

Logarithmic units simplify calculations for cascaded elements, turning multiplications into additions.

10.3.3 Polarisation-Maintaining Fibre

Standard single-mode fibres can exhibit random birefringence due to imperfections or stress, leading to a change in the polarisation state of light as it propagates. To maintain a specific input polarisation state throughout the fibre, Polarisation-Maintaining Fibres (PMFs) are used. These fibres have a controlled, strong internal birefringence intentionally introduced into their structure, for instance by using an elliptical core or by incorporating stress-applying elements alongside the core. This creates two well-defined principal polarisation axes (fast and slow). Light linearly polarised along one of these principal axes will largely maintain its polarisation state during propagation. Usually, the slow axis is used for launching light as it can be more robust against minor external perturbations.